Spherical-Multipole Analysis of the Scalar Diffraction by a Circular Aperture in a Plane Screen

The paper deals with a new spherical-multipole solution for the scattering of an arbitrary incident wave by a circular aperture in an acoustically soft or hard plane. The boundary-value problem is formulated as a three-domain problem. In each of the domains the field is expanded by means of a complete spherical-multipole expansion, which automatically satisfies the soft or hard boundary condition on the plane, if applicable. The multipole amplitudes of the incident field in the presence of the soft or hard plane are supposed to be given and explicitly derived for a plane wave and for a uniform Complex-Source Beam (CSB). The unknown multipole amplitudes are found from the conditions of continuity of the field and its normal derivative at the boundaries between the domains, leading to a quadratic system of linear equations. All coupling integrals are solved completely analytically. Possible and expected zeros and singularities of the field values or their derivatives at the rim of the aperture develop in the course of an increasing number of multipoles, while at the other locations a finite number of multipoles is sufficient to represent the field. The numerical evaluation validates and improves numerical results found in the literature for the geometrically complementary case of acoustically hard and soft circular discs. Further numerical results for the near- and far field exemplarily prove the robustness and convergence of the proposed method.

1 Introduction

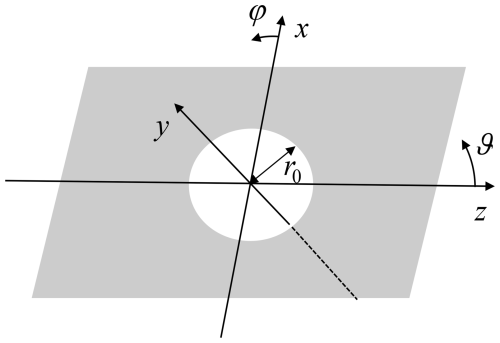
Scattering and diffraction by a circular aperture in an infinitely thin impenetrable screen as shown in Fig. 1 is one of the classical canonical problems in acoustics and electromagnetics. The interest in this structure stems from both, theoretical and practical reasons. Examples for the latter are the wave coupling between hollow wave guides in microwave engineering and the analysis of the influence of apertures in EMC shielding structures, among others. From the theoretical side this structure contains a geometrical singularity at the rim of the aperture which usually implies a certain singularity of the field. Moreover, the scattering problem is a favourite example for the application of Babinet's principle, i.e., meaning that the scattered field in the region “behind” the circular aperture (y<0 in Fig. 1) of radius r₀ in an acoustically soft (hard) plane is identical to the scattered field behind a circular disc of same radius r₀ consisting of an acoustically hard (soft) material. For the disc, exact analytic solutions of the corresponding acoustic boundary-value problems can be found by solving the Helmholtz equation in oblate spheroidal coordinates where the disc is one of the coordinate surfaces. Probably because of this principle and because of the finiteness of the corresponding problem, many of the solutions and numerical results found in the literature are derived for the circular disc and then adapted to the circular aperture.

Figure 1 Circular aperture in a plane screen at y=0.

Among the chronologically first attempts for a solution of an “electric” wave incident upon a circular aperture was the one presented by Rayleigh (1897). Much later Bowkamp (1941) exactly solved the disc problem analytically using spheroidal wave functions and also presented first numerical results. Bethe (1944) published a work on the diffraction by small holes and applied it to the directive coupling between wave guides (Bethe coupler) in microwave engineering. An insightful discussion of the field singularities at geometrical singularities like an edge or – as in the current case – a sharp rim including a discussion of the work by Bethe (1944) has been contributed again by Bouwkamp (1946). A direct solution of the scalar aperture problem via an integral equation formulation and a corresponding variational solution for the circular aperture in an infinite screen has been derived and presented in Levine and Schwinger (1948a) and Levine and Schwinger (1948b). Numerical results have been successfully compared to those ones given by Bowkamp (1941). The works by Meixner (1948) and Andrejewski (1953) solved the vector (electromagnetic) disc and aperture problem, respectively, emphasizing the role of the singularities for the unique solution of the boundary-value problem. The Meixner's edge condition states that the solution must include a certain type (degree) of singularity at the rim. Actually, while expanding the field by means of an infinite series solution which not explicitly contains this singularity, it must be developing term-by-term such that the correct singularity would be obtained only for an infinite number of terms. Braunbek (1950) applied an asymptotic method to the problem of an acoustically hard disc illuminated by a plane wave and showed that the method works fine for an surprisingly wide frequency range. De Hoop (1954) successfully investigated an approximate result derived by Bowkamp (1941). An aperture in an infinitely thin screen is also an excellent object to investigate the ability of high-frequency asymptotic methods, as has been shown in Keller (1957) and Keller et al. (1957), where the Geometrical Theory of Diffraction has been applied and tested to find an approximate solution. In Kristenssen and Waterman (1982) the exact solution using oblate spheroidal coordinates for the scalar disc problem was combined with the T-matrix method to make the disc and the aperture solutions accessible as part of more complex problems. Recently in Kurykiak and Lysechko (2015) the soft disc problem has been treated as a three-domain problem, where the analytically obtained final system of linear equations has been solved using an appropriate regularization approach.

The present paper deals with a new analytical approach to directly tackle the aperture problem. To this end, a three-domain boundary-value is formulated and corresponding spherical-multipole expansion have been formulated for both, an aperture in an acoustically soft or hard plane. The boundary-conditions are automatically satisfied by the chosen spherical-multipole functions. The unknown multipole amplitudes are found by enforcing the continuity of both, the wave functions and their derivatives. Finally a system of linear equations is obtained leading to convergent and consistent field solutions. Since the multipole expansions describing the field in the aperture do not explicitly contain any singularity or any zero field at the rim of the aperture, such a behaviour must be achieved while increasing the number of multipole amplitudes. The numerical evaluation includes a convergence analysis, a validation and several results for a plane wave as well as a uniform complex-source beam, each incident on a circular aperture in an acoustically soft and in an acoustically hard infinite screen. Besides the solution of a coupling integral with a product of two Ferrers functions with different degrees and orders, the appendix includes the derivation of the multipole amplitudes for an arbitrary incident plane wave and for a uniform complex-source beam, each in the presence of an acoustically soft or hard plane.

Parts of this work have been presented at conferences, see Klinkenbusch (2024a, b). A study on the corresponding 2D case (for the slit) has been published in Klinkenbusch (2019).

2 Formulation of the three-dimensional boundary-value problem

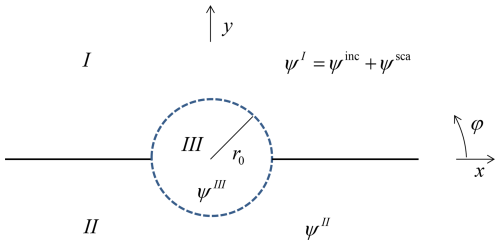
Consider a circular aperture in an infinitely extended acoustically soft or hard plane as sketched in Fig. 1. In Cartesian coordinates the plane is described by y=0 while the circular aperture of radius r₀ is symmetrically located around the origin. We introduce spherical coordinates $r,\mathit{\vartheta },\mathit{\phi }$ according to $x=r\sin \mathit{\vartheta }\cos \mathit{\phi },y=r\sin \mathit{\vartheta }\sin \mathit{\phi },z=r\cos \mathit{\vartheta }$ and split the entire space into three domains as shown in Fig. 2, with total fields ${\mathit{\psi }}^{\text{I}},{\mathit{\psi }}^{\text{II}},{\mathit{\psi }}^{\text{III}}$ in each domain. Domain I and II are defined by $r>r_{\mathrm{0}},y>\mathrm{0}$ and $r>r_{\mathrm{0}},y<\mathrm{0}$, respectively. Domain III consists of a sphere with radius r₀ centered at the origin and thus includes the entire aperture. In domain I we split the total field into a given incident (ψ^inc) and into a scattered (ψ^sca) part. The other domains are supposed to be source-free. In the following, we are seeking for time-harmonic solutions of the Helmholtz equation described by phasors at a time factor e^+jωt. We derive exact spherical-multipole expansions of the fields everywhere and for both cases, i.e., a circular aperture in a soft (index s) and in a hard (index h) infinite plane with ${\mathit{\psi }}_{\text{s}}^{\text{I}}{\mathrm{|}}_{y=\mathrm{0}}={\mathit{\psi }}_{\text{s}}^{\text{II}}{\mathrm{|}}_{y=\mathrm{0}}=\mathrm{0}$ and $\partial {\mathit{\psi }}_{\text{h}}^{\text{I}}/\partial \mathit{\phi }{\mathrm{|}}_{y=\mathrm{0}}=\partial {\mathit{\psi }}_{\text{h}}^{\text{II}}/\partial \mathit{\phi }{\mathrm{|}}_{y=\mathrm{0}}=\mathrm{0}$, respectively.

Figure 2 Definition of the three domains.

3 Solution of the boundary-value problem for a circular aperture in an acoustically soft plane

In each of the domains I, II we introduce a complete spherical-multipole expansion for the total field satisfying the boundary condition imposed by the acoustically soft plane, while the total field in domain III is developed by means of a general spherical-multipole expansion

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}{\mathit{\psi }}_{\text{s}}^{\text{I}}(r,\mathit{\vartheta },\mathit{\phi })& =\sum _{n=\mathrm{1}}^{n^{\text{inc}}}\sum _{m=\mathrm{1}}^n{a}_{nm}^{\text{inc}}{j}_n\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })\\ & +\sum _{n=\mathrm{1}}^{n^{\text{sca}}}\sum _{m=\mathrm{1}}^n{a}_{nm}^{\text{sca}}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })\end{array}\text{(2)}& {\displaystyle }{\mathit{\psi }}_{\text{s}}^{\text{II}}(r,\mathit{\vartheta },\mathit{\phi })=\sum _{n=\mathrm{1}}^{n^{\text{sca}}}\sum _{m=\mathrm{1}}^n{a}_{nm}^{\text{II}}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })\text{(3)}& {\displaystyle }\begin{array}{rl}{\mathit{\psi }}_{\text{s}}^{\text{III}}(r,\mathit{\vartheta },\mathit{\phi })& =\sum _{n=\mathrm{1}}^{n^{\text{III}}}\sum _{m=\mathrm{1}}^n{a}_{nm}^{\text{III}}{j}_n\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })\\ & +\sum _{n=\mathrm{0}}^{n^{\text{III}}}\sum _{m=\mathrm{0}}^n{b}_{nm}^{\text{III}}{j}_n\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi }).\end{array}\end{array}$$

Note that in addition in domain I the field is splitted into a (known) incident and a scattered part, each satisfying the boundary condition on the plane. In Eqs. (1)–(3), j_n and $h_n^{\left(\mathrm{2}\right)}$ represent spherical Bessel functions of the first kind and spherical Hankel functions of the second kind, to guarantee regularity everywhere and to comply with the Sommerfeld radiation condition, respectively. For an exact solution the upper limits of the sums in Eqs. (1)–(3), n^inc,n^sca, and n^III, in general each have to become infinitely large. The normalized odd [index (o)] and even [index (e)] surface-spherical harmonics are defined by

$$\begin{array}{}\text{(4)}& {\displaystyle }{Y}_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })& {\displaystyle }=\sqrt{{\displaystyle \frac{\mathrm{2}n+\mathrm{1}}{\mathrm{2}\mathit{\pi }}}{\displaystyle \frac{(n-m)\mathrm{!}}{(n+m)\mathrm{!}}}}{P}_n^m\left(\cos \mathit{\vartheta }\right)\sin \left(m\mathit{\phi }\right)\text{(5)}& {\displaystyle }{Y}_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })& {\displaystyle }=\sqrt{{\displaystyle \frac{\mathrm{2}n+\mathrm{1}}{\mathrm{2}\mathit{\pi }{\mathit{ϵ}}_m}}{\displaystyle \frac{(n-m)\mathrm{!}}{(n+m)\mathrm{!}}}}{P}_n^m\left(\cos \mathit{\vartheta }\right)\cos \left(m\mathit{\phi }\right)\end{array}$$

where $P_n^m$ denotes a Ferrers' function, i.e., an associated Legendre function of the first kind “on the cut”, see DLMF (2024), and where the Neumann number is given by ϵ_m=2 if m=0 and ϵ_m=1 if $m=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{\dots }$. On a closed spherical surface the surface spherical harmonics form a complete orthonormalized system for any solution of the Helmholtz operator according to

$$\begin{array}{}\text{(6)}& {\displaystyle }\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{Y}_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })\sin \mathit{\vartheta }\mathrm{d}\mathit{\vartheta }\mathrm{d}\mathit{\phi }={\mathit{\delta }}_{n{n}^{\prime }}{\mathit{\delta }}_{m{m}^{\prime }}\text{(7)}& {\displaystyle }\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{Y}_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })\sin \mathit{\vartheta }\mathrm{d}\mathit{\vartheta }\mathrm{d}\mathit{\phi }={\mathit{\delta }}_{n{n}^{\prime }}{\mathit{\delta }}_{m{m}^{\prime }}\text{(8)}& {\displaystyle }\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{Y}_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })\sin \mathit{\vartheta }\mathrm{d}\mathit{\vartheta }\mathrm{d}\mathit{\phi }=\mathrm{0}\text{(9)}& {\displaystyle }\begin{array}{rl}& \sum _{n=\mathrm{0}}^{\mathrm{\infty }}\sum _{m=\mathrm{0}}^n\left[Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(o)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })+Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(e)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\right]\\ & \widehat{=}{\displaystyle \frac{\mathit{\delta }(\mathit{\vartheta }-{\mathit{\vartheta }}^{\prime })\mathit{\delta }(\mathit{\phi }-{\mathit{\phi }}^{\prime })}{\sin \mathit{\vartheta }}}\end{array}\end{array}$$

with the Dirac δ-functional δ(x) and the Kronecker symbol defined by δ_ij=1 if i=j and δ_ij=0 if i≠j. Since (throughout the paper) an arbitrary incident field in domain I in defined as the field in the presence of the acoustically soft plane at y=0, it includes the reflected field and differs from the classical definition of the incident field in scattering problems. We anticipate that the multipole amplitudes of such an incident field are known, examples are represented in Appendix B and C. For the determination of all other multipole coefficients we have to consider the boundary- and continuity conditions. In particular, at the boundary at r=r₀, the total fields as well as their normal derivatives have to be continuous

$$\begin{array}{}\text{(10)}& {\displaystyle }{\left.{\mathit{\psi }}_{\text{s}}^{\text{III}}\right|}_{r=r_{\mathrm{0}}}=\left\{\begin{array}{ll}{\left.{\mathit{\psi }}_{\text{s}}^{\text{I}}\right|}_{r=r_{\mathrm{0}}}& \mathrm{0}<\mathit{\vartheta }<\mathit{\pi };\mathrm{0}<\mathit{\phi }<\mathit{\pi }\\ {\left.{\mathit{\psi }}_{\text{s}}^{\text{II}}\right|}_{r=r_{\mathrm{0}}}& \mathrm{0}<\mathit{\vartheta }<\mathit{\pi };\mathit{\pi }<\mathit{\phi }<\mathrm{2}\mathit{\pi }\end{array}\right.\text{(11)}& {\displaystyle }{\left.{\displaystyle \frac{\partial {\mathit{\psi }}_{\text{s}}^{\text{III}}}{\partial r}}\right|}_{r=r_{\mathrm{0}}}=\left\{\begin{array}{ll}{\left.\frac{\partial {\mathit{\psi }}_{\text{s}}^{\text{I}}}{\partial r}\right|}_{r=r_{\mathrm{0}}}& \mathrm{0}<\mathit{\vartheta }<\mathit{\pi };\mathrm{0}<\mathit{\phi }<\mathit{\pi }\\ {\left.\frac{\partial {\mathit{\psi }}_{\text{s}}^{\text{II}}}{\partial r}\right|}_{r=r_{\mathrm{0}}}& \mathrm{0}<\mathit{\vartheta }<\mathit{\pi };\mathit{\pi }<\mathit{\phi }<\mathrm{2}\mathit{\pi }.\end{array}\right.\end{array}$$

We insert Eqs. (1)–(3) into Eq. (10), multiply the result by $Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}}\sin \mathit{\vartheta }$, integrate on the interval $\mathrm{0}<\mathit{\vartheta }<\mathit{\pi };\mathrm{0}<\mathit{\phi }<\mathrm{2}\mathit{\pi }$, and finally obtain because of the orthogonality relations Eqs. (6)–(8)

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{a}_{nm}^{\text{III}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)& =\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{inc}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{inc}}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}\\ & +\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{sca}}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}\\ & +\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{II}}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{2}}\\ & (n=\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\text{III}};m=\mathrm{1},\mathrm{2},\mathrm{\dots },n).\end{array}\end{array}$$

In Eq. (12) and in the following the scalar products are defined according to

$$\begin{array}{}\text{(13)}& {\displaystyle }<Y_{nm},Y_{n^{\prime }{m}^{\prime }}{>}_{\mathrm{1}}=\underset{\mathit{\vartheta }=\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathit{\phi }=\mathrm{0}}{\overset{\mathit{\pi }}{\int }}{Y}_{nm}{Y}_{n^{\prime }{m}^{\prime }}\sin \mathit{\vartheta }\mathrm{d}\mathit{\vartheta }\mathrm{d}\mathit{\phi }\text{(14)}& {\displaystyle }<Y_{nm},Y_{n^{\prime }{m}^{\prime }}{>}_{\mathrm{2}}=\underset{\mathit{\vartheta }=\mathrm{0}}{\overset{\mathit{\pi }}{\int }}\underset{\mathit{\phi }=\mathit{\pi }}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{Y}_{nm}{Y}_{n^{\prime }{m}^{\prime }}\sin \mathit{\vartheta }\mathrm{d}\mathit{\vartheta }\mathrm{d}\mathit{\phi }.\end{array}$$

Next, multiplying Eq. (10) by $Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}}\sin \mathit{\vartheta }$ and integrating on $\mathrm{0}<\mathit{\vartheta }<\mathit{\pi };\mathrm{0}<\mathit{\phi }<\mathrm{2}\mathit{\pi }$ leads to

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{b}_{nm}^{\text{III}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)& =\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{inc}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{inc}}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}\\ & +\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{sca}}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}\\ & +\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{II}}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{2}}\\ & (n=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\text{III}};m=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n)\end{array}\end{array}$$

Correspondingly, inserting Eqs. (1)–(3) into Eq. (11) and multiplying the result subsequently by $Y_{nm}^{\text{(o)}}\sin \mathit{\vartheta }$ and by $Y_{nm}^{\text{(e)}}\sin \mathit{\vartheta }$ and each integrating on $\mathrm{0}<\mathit{\vartheta }<\mathit{\pi };\mathrm{0}<\mathit{\phi }<\mathrm{2}\mathit{\pi }$ yields

$$\begin{array}{}\text{(16)}& \begin{array}{rl}& a_{nm}^{\text{III}}{\left.{\displaystyle \frac{\mathrm{d}{j}_n\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}=\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{inc}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{inc}}{\left.{\displaystyle \frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\\ & <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}+\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{sca}}{\left.{\displaystyle \frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\\ & <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}+\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{II}}{\left.{\displaystyle \frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\\ & <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{2}}(n=\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\text{III}};m=\mathrm{1},\mathrm{2},\mathrm{\dots },n)\end{array}\end{array}$$

and

$$\begin{array}{}\text{(17)}& \begin{array}{rl}& b_{nm}^{\text{III}}{\left.{\displaystyle \frac{\mathrm{d}{j}_n\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}=\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{inc}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{inc}}{\left.{\displaystyle \frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\\ & <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}+\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{sca}}{\left.{\displaystyle \frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\\ & <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}+\sum _{n^{\prime }=\mathrm{1}}^{n^{\text{sca}}}\sum _{m^{\prime }=\mathrm{1}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{II}}{\left.{\displaystyle \frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\\ & <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{2}}(n=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\text{III}};m=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n),\end{array}\end{array}$$

respectively. As easily can be shown it holds

$$\begin{array}{}\text{(18)}& <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}=<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\delta }}_{n,n^{\prime }}{\mathit{\delta }}_{m,m^{\prime }}.\end{array}$$

Hence it follows from Eqs. (12) and (16) that

$$\begin{array}{}\text{(19)}& \begin{array}{rl}& a_{nm}^{\text{III}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[a_{nm}^{\text{inc}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)+a_{nm}^{\text{sca}}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right.\\ & \left.+a_{nm}^{\text{II}}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right](n=\mathrm{1},\mathrm{2},\mathrm{\dots };m=\mathrm{1},\mathrm{2},\mathrm{\dots },n)\end{array}\end{array}$$

and

$$\begin{array}{}\text{(20)}& \begin{array}{rl}& a_{nm}^{\text{III}}{\left.{\displaystyle \frac{\mathrm{d}{j}_n\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[a_{nm}^{\text{inc}}{\left.{\displaystyle \frac{\mathrm{d}{j}_n\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\right.\\ & \left.+a_{nm}^{\text{sca}}{\left.{\displaystyle \frac{\mathrm{d}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}+a_{nm}^{\text{II}}{\left.{\displaystyle \frac{\mathrm{d}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\right]\\ & (n=\mathrm{1},\mathrm{2},\mathrm{\dots };m=\mathrm{1},\mathrm{2},\mathrm{\dots },n)\end{array}\end{array}$$

We multiply Eq. (19) by ${\left.\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}\right|}_{r=r_{\mathrm{0}}}$ and subtract from the results the product of Eq. (20) and j_n(κr₀)

$$\begin{array}{}\text{(21)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[a_{nm}^{\text{sca}}+a_{nm}^{\text{II}}\right]\left[h_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right){\left.{\displaystyle \frac{\mathrm{d}{j}_n\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}\right.\\ & \left.-{\left.{\displaystyle \frac{\mathrm{d}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)}{\mathrm{d}\mathit{\kappa }r}}\right|}_{r=r_{\mathrm{0}}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right]=\mathrm{0}.\end{array}\end{array}$$

Because the Wronski determinant of a fundamental system has no zeroes we conclude from Eq. (21)

$$\begin{array}{}\text{(22)}& a_{nm}^{\text{sca}}=-a_{nm}^{\text{II}},\end{array}$$

which reflects the symmetry of the scattered fields (according to the current definition of the incident field which includes the reflected field) with respect to the plane y=0. Moreover, with Eq. (22) we immediately derive from Eq. (19)

$$\begin{array}{}\text{(23)}& a_{nm}^{\text{III}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{a}_{nm}^{\text{inc}}.\end{array}$$

As can be easily shown it holds

$$\begin{array}{}\text{(24)}& \begin{array}{rl}& <Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}=-<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{2}}\\ & =N_{nm,n^{\prime }{m}^{\prime }}\underset{-\mathrm{1}}{\overset{\mathrm{1}}{\int }}{P}_n^m\left(x\right)P_{n^{\prime }}^{m^{\prime }}\left(x\right)\mathrm{d}x\left\{\begin{array}{ll}\frac{\mathrm{2}{m}^{\prime }}{{m^{\prime }}^{\mathrm{2}}-m^{\mathrm{2}}}& \begin{array}{c}{m}^{\prime }-m\\ n^{\prime }-n\end{array}\text{odd}\\ \mathrm{0}& \text{else,}\end{array}\right..\end{array}\end{array}$$

where the normalization constant is given by

$$\begin{array}{}\text{(25)}& N_{nm,n^{\prime }{m}^{\prime }}=\sqrt{{\displaystyle \frac{(\mathrm{2}n+\mathrm{1})(\mathrm{2}{n}^{\prime }+\mathrm{1})}{\mathrm{4}{\mathit{\pi }}^{\mathrm{2}}{\mathit{ϵ}}_m}}{\displaystyle \frac{(n-m)\mathrm{!}(n^{\prime }-m^{\prime })\mathrm{!}}{(n+m)\mathrm{!}(n^{\prime }+m^{\prime })\mathrm{!}}}}.\end{array}$$

Moreover, the remaining integral in Eq. (24) can also be analytically solved in a closed form. As shown in Appendix A it holds

$$\begin{array}{}\text{(26)}& \begin{array}{rl}& \underset{-\mathrm{1}}{\overset{+\mathrm{1}}{\int }}{P}_n^m\left(x\right)P_{n^{\prime }}^{m^{\prime }}\left(x\right)\mathrm{d}x\\ & =\left\{\begin{array}{l}{\sum }_{p=\mathrm{0}}^{p_{\max }}{\sum }_{p^{\prime }=\mathrm{0}}^{p_{\max }^{\prime }}{\mathit{\alpha }}_{n,m}^p{\mathit{\alpha }}_{n^{\prime },m^{\prime }}^{p^{\prime }}\\ \frac{\mathrm{\Gamma }\left[\frac{\mathrm{1}}{\mathrm{2}}(n-n^{\prime }-m-m^{\prime }-\mathrm{2}p-\mathrm{2}{p}^{\prime }+\mathrm{1})\right]\mathrm{\Gamma }\left[\frac{\mathrm{1}}{\mathrm{2}}(m+m^{\prime }+\mathrm{2}p+\mathrm{2}{p}^{\prime }+\mathrm{2})\right]}{\mathrm{\Gamma }\left[\frac{\mathrm{1}}{\mathrm{2}}(n+n^{\prime }+\mathrm{3})\right]}\\ n+m+n^{\prime }+m^{\prime }\text{ even}\\ \mathrm{0}\text{ else,}\end{array}\right.\end{array}\end{array}$$

where Γ(x) represents the Gamma function and where

$$\begin{array}{}\text{(27)}& {\displaystyle }{\mathit{\alpha }}_{n,m}^p={\displaystyle \frac{(-\mathrm{1}{)}^{p+m}(n+m)\mathrm{!}}{{\mathrm{2}}^{m+\mathrm{2}p}(m+p)\mathrm{!}p\mathrm{!}(n-m-\mathrm{2}p)\mathrm{!}}},\text{(28)}& {\displaystyle }{p}_{\max }=\lfloor {\displaystyle \frac{n-m}{\mathrm{2}}}\rfloor p_{\max }^{\prime }=\lfloor {\displaystyle \frac{n^{\prime }-m^{\prime }}{\mathrm{2}}}\rfloor .\end{array}$$

In Eq. (28), ⌊x⌋ represents the largest integer ≤x. Now multiplying Eq. (15) by $\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}$ and subtracting from the result the product of Eq. (17) and j_n(κr₀) we derive with Eq. (22) and Eq. (24)

$$\begin{array}{}\text{(29)}& \begin{array}{rl}& \mathrm{2}\sum _{\begin{array}{c}n=\mathrm{1}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{sca}}}\sum _{\begin{array}{c}m=\mathrm{1}\\ m-m^{\prime }\\ \text{odd}\end{array}}^n{a}_{nm}^{\text{sca}}<Y_{nm}^{\text{(o)}},Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}}{>}_{\mathrm{1}}\\ & \left[{\displaystyle \frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)-j_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right){\displaystyle \frac{\mathrm{d}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}\right]\\ & =-\sum _{\begin{array}{c}n=\mathrm{1}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{inc}}}\sum _{\begin{array}{c}m=\mathrm{1}\\ m-m^{\prime }\\ \text{odd}\end{array}}^n{a}_{nm}^{\text{inc}}<Y_{nm}^{\text{(o)}},Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}}{>}_{\mathrm{1}}\\ & \left[j_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right){\displaystyle \frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}-{\displaystyle \frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right]\\ & (n^{\prime }=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\text{III}};m^{\prime }=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\prime }),\end{array}\end{array}$$

which can be written as a finite system of linear equations to determine the $a_{nm}^{\text{sca}}$ from the $a_{nm}^{\text{inc}}$

$$\begin{array}{}\text{(30)}& \left(\begin{array}{ccccc}{A}_{\mathrm{00},\mathrm{11}}& A_{\mathrm{00},\mathrm{21}}& A_{\mathrm{00},\mathrm{22}}& \mathrm{\dots }& A_{\mathrm{00},NN}\\ A_{\mathrm{10},\mathrm{11}}& A_{\mathrm{10},\mathrm{21}}& A_{\mathrm{10},\mathrm{22}}& \mathrm{\dots }& A_{\mathrm{10},NN}\\ A_{\mathrm{11},\mathrm{11}}& A_{\mathrm{11},\mathrm{21}}& A_{\mathrm{11},\mathrm{22}}& \mathrm{\dots }& A_{\mathrm{11},NN}\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}\\ A_{MM,\mathrm{11}}& A_{MM,\mathrm{21}}& A_{MM,\mathrm{22}}& \mathrm{\dots }& A_{MM,NN}\end{array}\right)\left(\begin{array}{c}{a}_{\mathrm{11}}^{\text{sca}}\\ a_{\mathrm{21}}^{\text{sca}}\\ a_{\mathrm{22}}^{\text{sca}}\\ \mathrm{⋮}\\ a_{NN}^{\text{sca}}\end{array}\right)=\left(\begin{array}{c}{A}_{\mathrm{00}}^{\text{inc}}\\ A_{\mathrm{10}}^{\text{inc}}\\ A_{\mathrm{11}}^{\text{inc}}\\ \mathrm{⋮}\\ A_{MM}^{\text{inc}}\end{array}\right).\end{array}$$

The elements of the matrix in Eq. (30) are found as

$$\begin{array}{}\text{(31)}& \begin{array}{rl}& A_{nm,n^{\prime }{m}^{\prime }}=\\ & \left\{\begin{array}{l}\mathrm{2}<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}\\ \left[h_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}-\frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right]& \begin{array}{c}n-n^{\prime }\text{odd}\\ \text{and}\\ m-m^{\prime }\text{odd}\end{array}\\ \mathrm{0}& \text{else,}\end{array}\right.\end{array}\end{array}$$

while for the elements of the right-hand side we obtain

$$\begin{array}{}\text{(32)}& A_{nm}^{\text{inc}}=\left\{\begin{array}{l}-{\sum }_{\begin{array}{c}{n}^{\prime }=\mathrm{1}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{inc}}}{\sum }_{\begin{array}{c}{m}^{\prime }=\mathrm{1}\\ m-m^{\prime }\\ \text{odd}\end{array}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{inc}}<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}\\ \left[j_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}-\frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right]& \begin{array}{c}n-n^{\prime }\text{odd}\\ \text{and}\\ m-m^{\prime }\text{odd}\end{array}\\ \mathrm{0}& \text{else.}\end{array}\right.\end{array}$$

For a quadratic system of linear equations in Eq. (30) we choose for the upper limits

$$\begin{array}{}\text{(33)}& N=n^{\text{sca}};M=n^{\text{III}}=n^{\text{sca}}-\mathrm{1}.\end{array}$$

Note that this kind of determination of the multipole amplitudes via a dense system of linear equations is referred to as being “non-final”, see Sommerfeld (1947). A change of the maximum number of scattered-field multipoles leads to a different degree of the system of linear equations and thus potentially changes all scattered-field multipole amplitudes.

Finally, with Eq. (22) the remaining multipole amplitudes in domain III can be found from Eqs. (15) and (17) according to

$$\begin{array}{}\text{(34)}& \begin{array}{rl}& b_{nm}^{\text{III}}={\displaystyle \frac{\mathrm{1}}{j_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)+\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}}\\ & \left\{\sum _{\begin{array}{c}{n}^{\prime }=\mathrm{1}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{inc}}}\sum _{\begin{array}{c}{m}^{\prime }=\mathrm{1}\\ m-m^{\prime }\\ \text{odd}\end{array}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{inc}}\left(j_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)+{\displaystyle \frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}\right.\\ & +\mathrm{2}\sum _{\begin{array}{c}{n}^{\prime }=\mathrm{1}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{sca}}}\sum _{\begin{array}{c}{m}^{\prime }=\mathrm{1}\\ m-m^{\prime }\\ \text{odd}\end{array}}^{n^{\prime }}{a}_{n^{\prime }{m}^{\prime }}^{\text{sca}}\left(h_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)+{\displaystyle \frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(o)}},\\ & \left.Y_{nm}^{\text{(e)}}{>}_{\mathrm{1}}\right\}(n=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\text{III}};m=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots },n).\end{array}\end{array}$$

Note that the attempt to determine the $b_{nm}^{\text{III}}$ just from Eq. (15) or from Eq. (17) would be not defined for the resonance cases, i.e., for the zeros of the spherical Bessel functions or of their derivatives, respectively. Finally, using the asymptotic expression of the spherical Hankel function of the second kind for large values of its argument

$$\begin{array}{}\text{(35)}& h_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)\cong j^{n+\mathrm{1}}{\displaystyle \frac{e^{-j\mathit{\kappa }r}}{\mathit{\kappa }r}},\end{array}$$

we define the far-field in domain II from Eqs. (2) and (35) dropping the spherical-wave term;

$$\begin{array}{}\text{(36)}& {\mathit{\psi }}_{\text{s},\mathrm{\infty }}^{\text{II}}(r,\mathit{\vartheta },\mathit{\phi })=\sum _{n=\mathrm{1}}^{n^{\text{sca}}}\sum _{m=\mathrm{1}}^n{j}^{n+\mathrm{1}}{a}_{nm}^{\text{II}}{Y}_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi }).\end{array}$$

4 Solution of the boundary-value problem for a circular aperture in an acoustically hard plane

In each of the domains I, II, and III we introduce a complete spherical-multipole expansion for the total field according to

$$\begin{array}{}\text{(37)}& {\displaystyle }\begin{array}{rl}{\mathit{\psi }}_{\text{h}}^{\text{I}}(r,\mathit{\vartheta },\mathit{\phi })& =\sum _{n=\mathrm{0}}^{n^{\text{inc}}}\sum _{m=\mathrm{0}}^n{b}_{nm}^{\text{inc}}{j}_n\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })\\ & +\sum _{n=\mathrm{0}}^{n^{\text{sca}}}\sum _{m=\mathrm{0}}^n{b}_{nm}^{\text{sca}}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })\end{array}\text{(38)}& {\displaystyle }{\mathit{\psi }}_{\text{h}}^{\text{II}}(r,\mathit{\vartheta },\mathit{\phi })=\sum _{n=\mathrm{0}}^{n^{\text{sca}}}\sum _{m=\mathrm{0}}^n{b}_{nm}^{\text{II}}{h}_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })\text{(39)}& {\displaystyle }\begin{array}{rl}{\mathit{\psi }}_{\text{h}}^{\text{III}}(r,\mathit{\vartheta },\mathit{\phi })& =\sum _{n=\mathrm{1}}^{n^{\text{III}}}\sum _{m=\mathrm{1}}^n{\mathit{\alpha }}_{nm}^{\text{III}}{j}_n\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })\\ & +\sum _{n=\mathrm{0}}^{n^{\text{III}}}\sum _{m=\mathrm{0}}^n{\mathit{\beta }}_{nm}^{\text{III}}{j}_n\left(\mathit{\kappa }r\right)Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi }).\end{array}\end{array}$$

Note that the incident field represented by the spherical multipole amplitudes $b_{nm}^{\text{inc}}$ again is defined as an arbitrary incident field in domain I in the presence of the acoustically hard plane at y=0, i.e., it includes the reflected field and thus differs from the classical definition of an incident field in scattering problems.

The multipole amplitudes of such an incident field $b_{nm}^{\text{inc}}$ are known. For the determination of the other multipole coefficients we have to consider the boundary- and continuity conditions according to Eqs. (10)–(11). A quite similar analysis as shown in Sect. 3 leads to the relations

$$\begin{array}{}\text{(40)}& b_{nm}^{\text{sca}}=-b_{nm}^{\text{II}}\end{array}$$

and

$$\begin{array}{}\text{(41)}& {\mathit{\beta }}_{nm}^{\text{III}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{b}_{nm}^{\text{inc}}.\end{array}$$

The multipole amplitudes of the scattered field are found from the solution of the system of linear equations

$$\begin{array}{}\text{(42)}& \left(\begin{array}{ccccc}{C}_{\mathrm{11},\mathrm{00}}& C_{\mathrm{11},\mathrm{10}}& C_{\mathrm{11},\mathrm{11}}& \mathrm{\dots }& C_{\mathrm{11},MM}\\ C_{\mathrm{21},\mathrm{00}}& C_{\mathrm{21},\mathrm{10}}& C_{\mathrm{21},\mathrm{11}}& \mathrm{\dots }& C_{\mathrm{21},MM}\\ C_{\mathrm{22},\mathrm{00}}& C_{\mathrm{22},\mathrm{10}}& C_{\mathrm{22},\mathrm{11}}& \mathrm{\dots }& C_{\mathrm{22},MM}\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}\\ C_{NN,\mathrm{00}}& C_{NN,\mathrm{10}}& C_{NN,\mathrm{11}}& \mathrm{\dots }& C_{NN,MM}\end{array}\right)\left(\begin{array}{c}{b}_{\mathrm{00}}^{\text{sca}}\\ b_{\mathrm{10}}^{\text{sca}}\\ b_{\mathrm{11}}^{\text{sca}}\\ \mathrm{⋮}\\ b_{MM}^{\text{sca}}\end{array}\right)=\left(\begin{array}{c}{D}_{\mathrm{11}}^{\text{inc}}\\ D_{\mathrm{21}}^{\text{inc}}\\ D_{\mathrm{22}}^{\text{inc}}\\ \mathrm{⋮}\\ D_{NN}^{\text{inc}}\end{array}\right).\end{array}$$

The elements of the matrix in Eq. (42) are given by

$$\begin{array}{}\text{(43)}& \begin{array}{rl}& C_{nm,n^{\prime }{m}^{\prime }}=\\ & \left\{\begin{array}{l}\mathrm{2}<Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}\times \\ \left[h_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}-\frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right]& \begin{array}{c}n-n^{\prime }\text{odd}\\ \text{and}\\ m-m^{\prime }\text{odd}\end{array}\\ \mathrm{0}& \text{else,}\end{array}\right.\end{array}\end{array}$$

while for the elements of the right-hand side we obtain

$$\begin{array}{}\text{(44)}& \begin{array}{rl}& D_{nm}^{\text{inc}}=\\ & \left\{\begin{array}{l}-{\sum }_{\begin{array}{c}{n}^{\prime }=\mathrm{0}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{inc}}}{\sum }_{\begin{array}{c}{m}^{\prime }=\mathrm{0}\\ m-m^{\prime }\\ \text{odd}\end{array}}^{n^{\prime }}{b}_{n^{\prime }{m}^{\prime }}^{\text{inc}}<Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}\times \\ \left[j_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}-\frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)\right]& \begin{array}{c}n-n^{\prime }\text{odd}\\ \text{and}\\ m-m^{\prime }\text{odd}\end{array}\\ \mathrm{0}& \text{else.}\end{array}\right.\end{array}\end{array}$$

For a quadratic system of linear equations in Eq. (42) we choose for the upper limits N=n^sca and $M=n^{\text{III}}=n^{\text{sca}}-\mathrm{1}$. The remaining multipole amplitudes in the domain III are then found according to

$$\begin{array}{}\text{(45)}& \begin{array}{rl}& {\mathit{\alpha }}_{nm}^{\text{III}}={\displaystyle \frac{\mathrm{1}}{j_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)+\frac{\mathrm{d}{j}_n\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}}\\ & \left\{\sum _{\begin{array}{c}{n}^{\prime }=\mathrm{0}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{inc}}}\sum _{\begin{array}{c}{m}^{\prime }=\mathrm{0}\\ m-m^{\prime }\\ \text{odd}\end{array}}^{n^{\prime }}{b}_{n^{\prime }{m}^{\prime }}^{\text{inc}}\left(j_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)+{\displaystyle \frac{\mathrm{d}{j}_{n^{\prime }}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}},Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}\right.\\ & +\mathrm{2}\sum _{\begin{array}{c}{n}^{\prime }=\mathrm{0}\\ n-n^{\prime }\\ \text{odd}\end{array}}^{n^{\text{sca}}}\sum _{\begin{array}{c}{m}^{\prime }=\mathrm{0}\\ m-m^{\prime }\\ \text{odd}\end{array}}^{n^{\prime }}{b}_{n^{\prime }{m}^{\prime }}^{\text{sca}}\left(h_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)+{\displaystyle \frac{\mathrm{d}{h}_{n^{\prime }}^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}_{\mathrm{0}}\right)}{\mathrm{d}\mathit{\kappa }{r}_{\mathrm{0}}}}\right)<Y_{n^{\prime }{m}^{\prime }}^{\text{(e)}},\\ & \left.Y_{nm}^{\text{(o)}}{>}_{\mathrm{1}}\right\}(n=\mathrm{1},\mathrm{2},\mathrm{\dots },n^{\text{III}};m=\mathrm{1},\mathrm{2},\mathrm{\dots },n).\end{array}\end{array}$$

Finally, the far-field in domain II is defined by

$$\begin{array}{}\text{(46)}& {\mathit{\psi }}_{\text{h},\mathrm{\infty }}^{\text{II}}(r,\mathit{\vartheta },\mathit{\phi })=\sum _{n=\mathrm{0}}^{n^{\text{sca}}}\sum _{m=\mathrm{0}}^n{j}^{n+\mathrm{1}}{b}_{nm}^{\text{II}}{Y}_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi }).\end{array}$$

5 Numerical Evaluation

5.1 Convergence

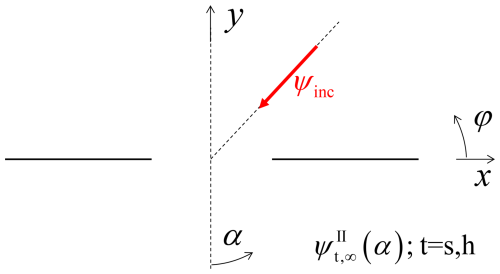
Since the maximum orders of the multipole expansions and thus the dimensions of the systems of linear equations involved in the solutions basically tend to infinity, the investigation of their convergence properties is of vital interest. Moreover, as the expansion in the inner domain III involves sharp geometrical singularities, it is not a-priori clear that we obtain a converging multipole expansion which is not explicitly including that singularity, at all. To investigate this exemplarily, we consider the geometry in Fig. 3 and the solution for a plane wave incident on an aperture in a plane with an acoustically soft boundary condition. The multipole amplitudes for a plane wave are derived in Appendix B. First, as seen from Eq. (33) the highest degree of the scattered fields n^sca in domains I and II is identical to the highest degree N=n^III of the multipole expansion in the inner domain III. In domain III we have an expansion with spherical Bessel functions, and for a “normal” problem (smooth scatterer) with an electric radius kr₀ of the minimum enclosing sphere, for a reasonable accuracy we would expect a highest relevant degree of about $N\approx k{r}_{\mathrm{0}}+\mathrm{6}$, leading to about N=12 for r₀=1λ, see Chew et al. (1998).

Figure 3 Geometry considered for the evaluation of the far-field scattered by the circular aperture.

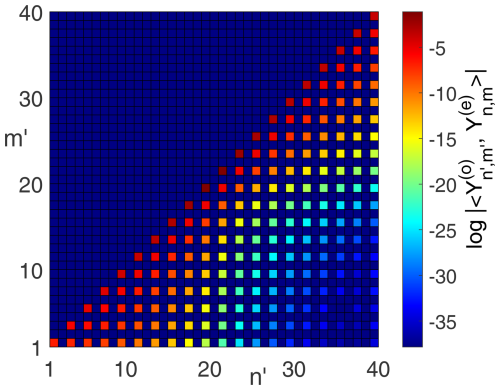
Second, for the coupling from the incident field multipole modes to the inner domain III the behaviour of the coupling integrals Eq. (24) is important. Exemplarily, Fig. 4 indicates that the maximum coupling is obtained for same orders, i.e., if n^III≈n^inc in this context. In other words, to obtain the correct right-hand side amplitudes in Eq. (32), we must choose n^inc sufficiently larger than N=n^sca.

Figure 4 Absolute value of the coupling integral (Eq. 24) for a fixed $n=\mathrm{20},m=\mathrm{10}$ as a function of $n^{\prime },m^{\prime }$.

Taking this into account we have computed and shown in Fig. 5 the far field for a plane wave scattered by an aperture with radius r₀=1λ for different maximum orders of N. n^inc has been chosen as 40, which turned out to be a sufficiently large number for the cases considered in the following.

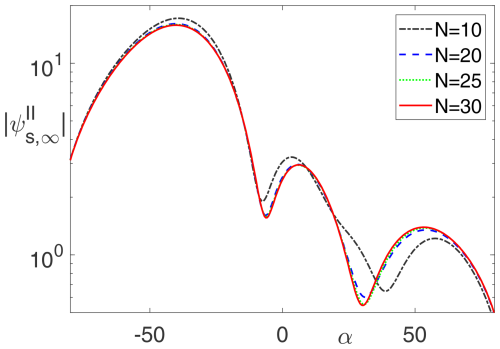
Figure 5 Scattered far field for a plane wave illuminating a circular aperture in an acoustically soft plane for different values of the maximum degree N=n^sca of the spherical-multipole expansion of the scattered field. Angle of incidence ϕ^inc=45°; Radius of the aperture: r₀=1λ; The maximum degree of the spherical-multipole expansion of the incident field has been chosen to n^inc=40; α is defined in Fig. 3.

As can be observed, a maximum order of N=30 turns out to yield convergent results. Note that this also exemplarily shows that this problem is solvable – on the cost of a significantly higher number of multipoles needed to represent the far field in domain II, as compared to a problem with a smooth scattering object of the same size.

5.2 Validation

In order to validate the results, Figs. 6 and 7 show the far fields in domain II for a plane wave symmetrically (with respect to the y axis and to the aperture) incident on a circular aperture of different radii. The outcomes of the present method are compared to those ones obtained for the case of a plane wave symmetrically incident on a disc of same size. By applying Babinet's principle we have to compare the results of a plane wave incident on an circular aperture in an acoustically soft plane to those ones of the same plane wave but incident on an acoustically hard disc of same size (and vice versa). The latter results have been obtained by means of exactly solving the Helmholtz equation in oblate ellipsoidal coordinates where the disc is a coordinate surface. These results are taken from Bowman et al. (1988).

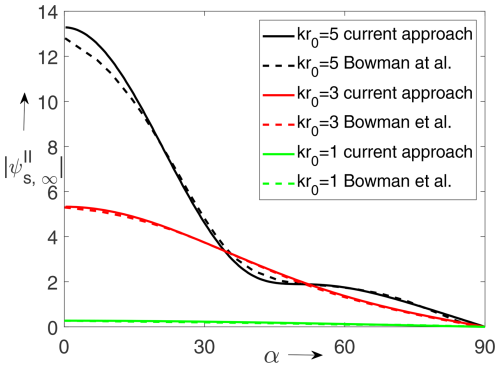
Figure 6 Plane wave symmetrically incident on a circular aperture of different radii in an acoustically soft screen. Present approach (solid line) and results taken from Bowman et al. (1988) for an acoustically hard disc; α is defined in Fig. 3.

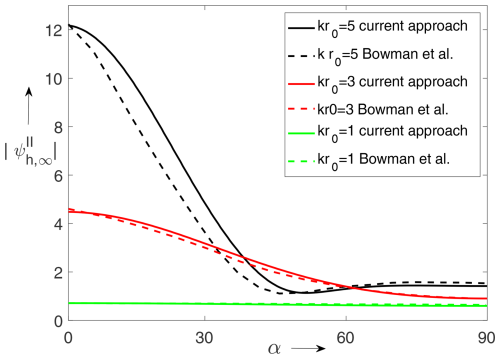
Figure 7 Plane wave symmetrically incident on a circular aperture of different radii in an acoustically hard screen. Present approach (solid line) and results taken from Bowman et al. (1988) for an acoustically soft disc; α is defined in Fig. 3.

Note that for both of the figures no further normalization (except of dropping the spherical-wave term) of the amplitude has been applied. While we observe a relatively good agreement for aperture (disc) radii kr₀=1 and kr₀=3, the differences increase for kr₀=5 particularly in the near of the symmetry axis (α=0). Because of the symmetry of the incident plane wave we expect a zero tangent of the curve for α=0, which quite obviously is not the case for the result taken from Bowman et al. (1988) rendering them as inaccurate.

5.3 Numerical results for an aperture in an acoustically soft screen

Figure 8 shows the real part of the phasor of the near field ψ_s. A plane wave is incident from φ^inc=45° on the aperture of radius r₀=1λ in an acoustically soft screen. Note that this is identical to a snapshot of the time-domain field at t=0. For y>0 we observe the typical interference pattern produced by the superposition of the incident and the reflected field, while for y<0 the typical diffraction pattern of an aperture can be observed. The field and its derivative is continuous for r=r₀ which also proves the convergence and consistency of the method for the numbers of multipoles chosen, and the correctness of the numerical implementation.

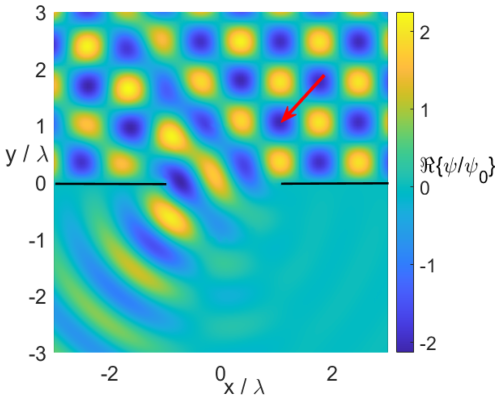
Figure 8 Plane wave incident on a circular aperture in an acoustically soft screen. Real part of the near field ψ_s(r). Radius of the aperture: r₀=1λ; ϕ^inc=45°; n^sc=30; n^inc=40.

In Fig. 9 we see the absolute amplitude of the field in the aperture for $y=z=\mathrm{0},-\mathrm{1}\mathit{\lambda }<x<\mathrm{1}\mathit{\lambda }$) for different values of n^III. Apart from the edge at r=r₀ the field converges well with a finite number of multipole amplitudes. At r=r₀ the field converges very slowly against zero which is expected as the field should be zero at the sharp rim only whereas it has to be non-zero and continuous for all other values.

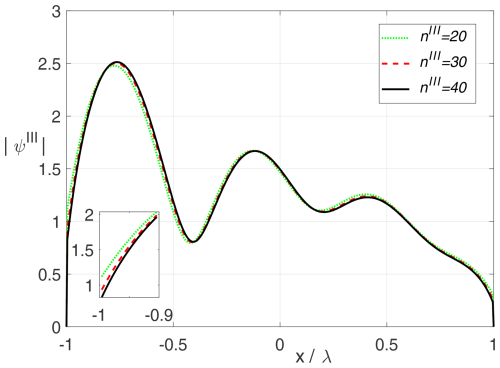
Figure 9 Absolute value of ${\mathit{\psi }}_s^{\text{III}}\left(\mathit{r}\right)$ in the aperture for ($y=z=\mathrm{0}$) as a function of x for different value of n^III. Plane wave incident (φ^inc=45°) on a circular aperture with radius r₀=1λ in an acoustically soft screen. n^inc=50.

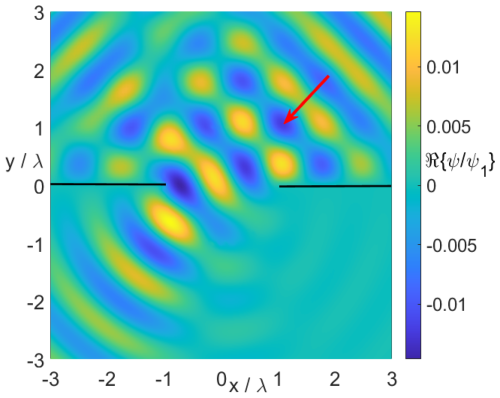
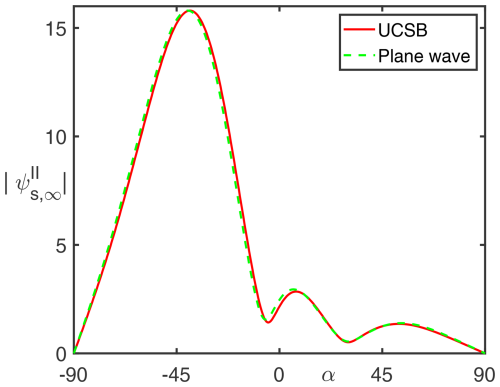
Figure 10 shows the near-field for the same geometry as in Fig. 8 but with an incident uniform Complex-Source Beam (uniform CSB). The derivation of the corresponding multipole amplitudes is attached in Appendix C. Since the waist of the uniform CSB has been located almost in the aperture and the beam width at the waist is $w_{\mathrm{0}}/\mathit{\lambda }=\mathrm{2}\sqrt{b/\mathit{\lambda }(\mathrm{1}/\mathit{\pi })}\approx \mathrm{3.57}$, the interaction between the uniform CSB in its waist and the aperture are expected to be quite similar as for a corresponding incident plane wave. Thus it is not surprising that the scattered far fields for both, an incident plane wave and an incident uniform CSB are essentially the same as shown in Fig. 11. Further note that the far-field results are much faster converging than the field at or nearby the rim ($r=r_{\mathrm{0}};y=\mathrm{0}$), see Fig. 9. The results also support the idea, that for the investigation of a local phenomenon of infinite semi-infinite structures (e.g., the tip of a semi-infinite cone) we may use a uniform CSB instead of a plane wave which leads to drastically reduced convergence problems of multipole expansions.

Figure 10 Uniform CSB incident on a circular aperture in an acoustically soft screen. Real part of the near field ψ_s(r). Radius of the aperture: r₀=1λ. Coordinates of the waist: $r_{\mathrm{w}}=\mathrm{0.01}\mathit{\lambda };{\mathit{\vartheta }}_{\mathrm{w}}=\mathrm{90}\mathit{°};{\mathit{\phi }}_{\mathrm{w}}=\mathrm{45}\mathit{°}$; Rayleigh length: b=10λ; $n^{\text{sc}}=\mathrm{30};n^{\text{inc}}=\mathrm{40}$.

Figure 11 Plane wave and uniform CSB incident on a circular aperture in an acoustically soft screen: Comparison of the scattered far fields ${\mathit{\psi }}_{\text{s},\mathrm{\infty }}^{\text{II}}$. r₀=1λ; ϕ^inc=45°; Coordinates of the waist: $r_{\mathrm{w}}=\mathrm{0.01}\mathit{\lambda };{\mathit{\vartheta }}_{\mathrm{w}}=\mathrm{90}\mathit{°};{\mathit{\phi }}_{\mathrm{w}}=\mathrm{45}\mathit{°}$; Rayleigh length: b=10λ; $n^{\text{sc}}=\mathrm{30};n^{\text{inc}}=\mathrm{40}$; α is defined in Fig. 3.

5.4 Numerical results for an aperture in an acoustically hard screen

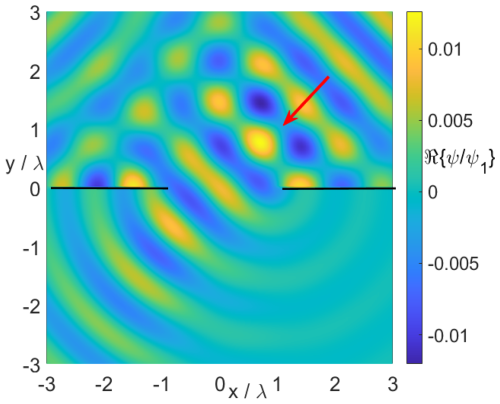
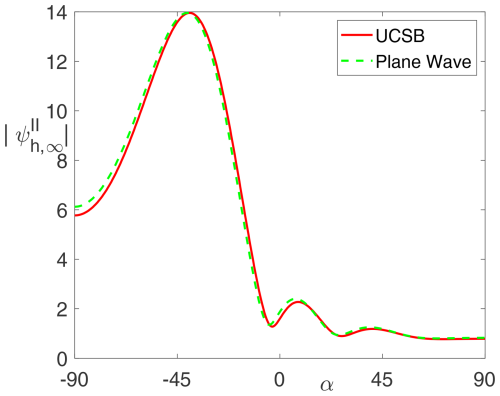
Figure 12 shows the real part of the field phasor for a plane wave incident on an aperture (radius r₀=1λ) in an acoustically hard plane. Figure 13 represents the corresponding absolute values of the normal field derivative in the aperture. We clearly observe an (expected) field singularity at the rim (r=r₀) which is more and more developed with an increasing number of multipoles n^III. In Fig. 14 we see the corresponding near-field for an incident uniform CSB, while finally Fig. 15 shows that the scattered far fields for both, an incident plane wave and an incident uniform CSB.

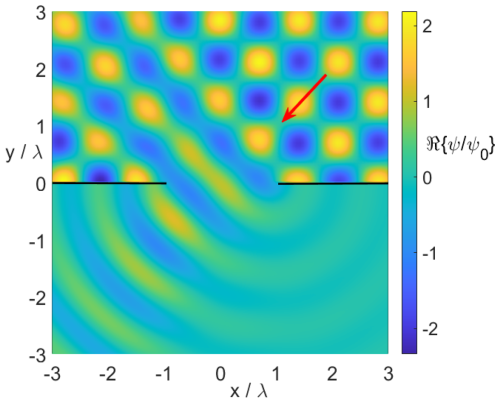
Figure 12 Plane wave incident on a circular aperture in an acoustically hard screen; φ^inc=45°. Real part of the near field ψ_h(r). r₀=1λ; $n^{\text{sc}}=\mathrm{30};n^{\text{inc}}=\mathrm{40}$.

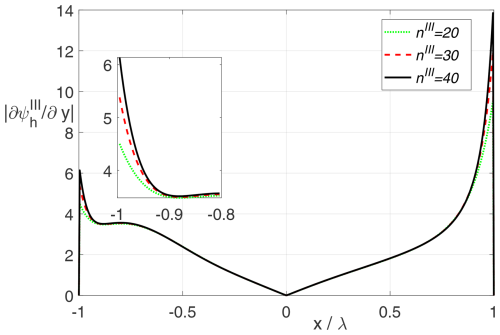
Figure 13 Plane wave incident on a circular aperture in an acoustically hard screen: Absolute value of the derivative $\partial {\mathit{\psi }}_h^{\text{III}}/\partial y$ in the aperture ($y=z=\mathrm{0}$) as a function of x for different values of n^III. φ^inc=45°); r₀=1λ; n^inc=50.

Figure 14 Uniform CSB incident on a circular aperture in an acoustically hard screen. Real part of the near field ψ_s(r). r₀=1λ; $n^{\text{sc}}=\mathrm{30};n^{\text{inc}}=\mathrm{40}$. Coordinates of the waist: $r_{\mathrm{w}}=\mathrm{0.01}\mathit{\lambda };{\mathit{\vartheta }}_{\mathrm{w}}=\mathrm{90}\mathit{°};{\mathit{\phi }}_{\mathrm{w}}=\mathrm{45}\mathit{°}$; Rayleigh length: b=10λ.

Figure 15 Plane wave and uniform CSB incident on a circular aperture in an acoustically hard screen: Scattered far field ${\mathit{\psi }}_{\text{s},\mathrm{\infty }}^{\text{II}}$. r₀=1λ; φ^inc=45°); Coordinates of the waist: $r_{\mathrm{w}}=\mathrm{0.01}\mathit{\lambda };{\mathit{\vartheta }}_{\mathrm{w}}=\mathrm{90}\mathit{°};{\mathit{\phi }}_{\mathrm{w}}=\mathrm{45}\mathit{°}$; Rayleigh length: b=10λ;$n^{\text{sc}}=\mathrm{30};n^{\text{inc}}=\mathrm{40}$; α is defined in Fig. 3.

6 Conclusions and Outlook

It has been shown that the classical canonical problem for an aperture in an acoustically soft or hard infinite plane screen can be solved analytically by means of a three-domain problem and suitable spherical-multipole expansions in each of the domains. All integrals which occur in the context of solving the boundary-value problems can be solved analytically. Moreover, the solution is performed by means of ordinary spherical coordinates and corresponding elementary solutions of the Helmholtz equation, i.e., spherical Bessel and Hankel functions and surface spherical harmonics with integer degrees and orders. Solutions of the Helmholtz equation in spheroidal wave functions and their sometimes as “difficult” reported numerical calculation (Zeppenfeld, 2009) are completely avoided. The resulting series solutions turn out to deliver correct results with a stable but comparatively slow convergence. The latter is mainly due to the fact that singular field values we expect at the rim of the aperture are not explicitly expressed by the series expansions but achieved for an infinite number of multipoles only. In contrast, for other observation points particularly in the far-field a limited number of multipoles is sufficient for any reasonable accuracy. Future research includes the further investigation of the outcome that for a field representation outside of the rim only a certain part of the modal expansion of the singularity is relevant. Moreover, future research includes the solution and analysis of the corresponding electromagnetic problem.

Appendix A: Analytical evaluation of the integral on a product of two Ferrers functions with different orders and degrees

The derivation follows that one given by Wong (1998). Since the result presented here slightly differs from the one given in Wong (1998) and some of the formulaes can not be found in the standard literature, the basic steps of the derivation are included in this work.

To analytically evaluate the integral

$$\begin{array}{}\text{(A1)}& I_{n,m;n^{\prime },m^{\prime }}=\underset{-\mathrm{1}}{\overset{+\mathrm{1}}{\int }}{P}_n^m\left(x\right)P_{n^{\prime }}^{m^{\prime }}\left(x\right)\mathrm{d}x\end{array}$$

we start from the representations of the associated Legendre function “on the cut”, also known as Ferrers' function, valid for integral values of n and m for a real-valued argument $-\mathrm{1}\le x\le +\mathrm{1}$

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}{P}_n^m\left(x\right)& =(-\mathrm{1}{)}^{m+n}{\displaystyle \frac{{\left(\mathrm{1}-x^{\mathrm{2}}\right)}^{m/\mathrm{2}}}{{\mathrm{2}}^{n}n\mathrm{!}}}{\displaystyle \frac{{\mathrm{d}}^{m+n}}{\mathrm{d}{x}^{m+n}}}{\left(\mathrm{1}-x^{\mathrm{2}}\right)}^n\\ & =\sum _{p=\mathrm{0}}^{p_{\text{max}}}{a}_{n,m}^p{\left(\mathrm{1}-x^{\mathrm{2}}\right)}^{\frac{m+\mathrm{1}}{\mathrm{2}}p}{x}^{n-m-\mathrm{2}p}\end{array}\end{array}$$

where

$$\begin{array}{}\text{(A3)}& {\displaystyle }{a}_{n,m}^p& {\displaystyle }={\displaystyle \frac{(-\mathrm{1}{)}^{m+p}(n+m)\mathrm{!}}{{\mathrm{2}}^{m+\mathrm{2}p}(m+p)\mathrm{!}p\mathrm{!}(n-m-\mathrm{2}p)\mathrm{!}}}\text{(A4)}& {\displaystyle }{p}_{\text{max}}& {\displaystyle }=\lfloor {\displaystyle \frac{n-m}{\mathrm{2}}}\rfloor .\end{array}$$

In Eq. (A4), ⌊x⌋ means the highest integer not larger than x. Inserting Eq. (A2) into Eq. (A1) yields

$$\begin{array}{}\text{(A5)}& \begin{array}{rl}& I_{n,m;n^{\prime },m^{\prime }}=\sum _{p=\mathrm{0}}^{p_{\text{max}}}{a}_{n,m}^p\sum _{p^{\prime }=\mathrm{0}}^{p_{\text{max}}^{\prime }}{a}_{n^{\prime },m^{\prime }}^{p^{\prime }}\underset{-\mathrm{1}}{\overset{+\mathrm{1}}{\int }}(\mathrm{1}-x^{\mathrm{2}}{)}^{\frac{m+\mathrm{2}p+m^{\prime }+\mathrm{2}{p}^{\prime }}{\mathrm{2}}}\\ & x^{n+n^{\prime }-m-m^{\prime }-\mathrm{2}p-\mathrm{2}{p}^{\prime }}\mathrm{d}x\\ & =\left\{\begin{array}{l}\mathrm{2}{\sum }_{p=\mathrm{0}}^{p_{\text{max}}}{a}_{n,m}^p{\sum }_{p^{\prime }=\mathrm{0}}^{p_{\text{max}}^{\prime }}{a}_{n^{\prime },m^{\prime }}^{p^{\prime }}{\int }_{\mathrm{0}}^{+\mathrm{1}}(\mathrm{1}-x^{\mathrm{2}}{)}^{\frac{m+\mathrm{2}p+m^{\prime }+\mathrm{2}{p}^{\prime }}{\mathrm{2}}}\\ x^{n+n^{\prime }-m-m^{\prime }-\mathrm{2}p-\mathrm{2}{p}^{\prime }}\mathrm{d}x\text{if}n+n^{\prime }-m-m^{\prime }\text{even}\\ \mathrm{0}\text{else.}\end{array}\right.\end{array}\end{array}$$

A comparison of the integral in Eq. (A5) with the definition of the Beta-function

$$\begin{array}{}\text{(A6)}& B(a,b)=\underset{\mathrm{0}}{\overset{+\mathrm{1}}{\int }}{t}^{a-\mathrm{1}}(\mathrm{1}-t^{\mathrm{2}}{)}^{b-\mathrm{1}}\mathrm{d}t={\displaystyle \frac{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{\mathrm{\Gamma }(a+b}}\end{array}$$

leads after a suitable substitution t=x² to the final result

$$\begin{array}{}\text{(A7)}& \begin{array}{rl}& I_{n,m;n^{\prime },m^{\prime }}=\\ & \left\{\begin{array}{l}{\sum }_{p=\mathrm{0}}^{p_{\text{max}}}{a}_{n,m}^p{\sum }_{p^{\prime }=\mathrm{0}}^{p_{\text{max}}^{\prime }}{a}_{n^{\prime },m^{\prime }}^{p^{\prime }}\\ \frac{\mathrm{\Gamma }\left[\frac{\mathrm{1}}{\mathrm{2}}(n+n^{\prime }-m-m^{\prime }-\mathrm{2}p-\mathrm{2}{p}^{\prime }+\mathrm{1})\right]\mathrm{\Gamma }\left[\frac{\mathrm{1}}{\mathrm{2}}(m+m^{\prime }+\mathrm{2}p+\mathrm{2}{p}^{\prime }+\mathrm{2})\right]}{\mathrm{\Gamma }\left[\frac{\mathrm{1}}{\mathrm{2}}(n+n^{\prime }+\mathrm{3})\right]}\\ \text{if}n+n^{\prime }-m-m^{\prime }\text{even}\\ \mathrm{0}\text{else.}\end{array}\right.\end{array}\end{array}$$

Appendix B: Spherical-multipole expansion of an arbitrary plane wave in the presence of a plane

In order to describe an arbitrarily incident plane wave propagating in the direction $-\widehat{n}$ in the presence of an acoustically soft or hard plane by means of a spherical-multipole expansion, we are looking for the multipole amplitudes $a_{nm}^{\text{inc}}$ and $b_{nm}^{\text{inc}}$ which satisfy the following relation

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}{\mathit{\psi }}^{\text{inc}}& =A_{\mathrm{0}}{e}^{j\mathit{\kappa }\widehat{n}\cdot \mathit{r}}=\sum _{n=\mathrm{0}}^{\mathrm{\infty }}\sum _{m=\mathrm{0}}^n{j}_n\left(\mathit{\kappa }r\right)\left[a_{nm}^{\text{inc}}{Y}_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })\right.\\ & \left.+b_{nm}^{\text{inc}}{Y}_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })\right]\end{array}\end{array}$$

To this end, we start from the comparison of the closed and bilinear forms of the free-space Green's function in case of $r<r^{\prime }$

$$\begin{array}{}\text{(B2)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{e^{-j\mathit{\kappa }\mathrm{|}\mathit{r}-{\mathit{r}}^{{}^{\prime }}\mathrm{|}}}{\mathrm{|}\mathit{r}-{\mathit{r}}^{{}^{\prime }}\mathrm{|}}}=-j\mathit{\kappa }\sum _{n=\mathrm{0}}^{\mathrm{\infty }}\sum _{m=\mathrm{0}}^n{j}_n\left(\mathit{\kappa }r\right)h_n^{\left(\mathrm{2}\right)}\left(\mathit{\kappa }{r}^{\prime }\right)\\ & \left[Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(o)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })+Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(e)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\right]\end{array}\end{array}$$

For $\mathit{\kappa }{r}^{\prime }\to \mathrm{\infty }$, a Taylor expansion of the left-hand side in Eq. (B2) and the asymptotic expression of the spherical Hankel function of the second kind [see Eq. (35)] yields

$$\begin{array}{}\text{(B3)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}}{e}^{-j\mathit{\kappa }{\widehat{r}}^{\prime }\cdot \mathit{r}}{\displaystyle \frac{e^{-j\mathit{\kappa }{r}^{\prime }}}{r^{\prime }}}=-j\mathit{\kappa }\sum _{n=\mathrm{0}}^{\mathrm{\infty }}\sum _{m=\mathrm{0}}^n{j}_n\left(\mathit{\kappa }r\right)(j{)}^{n+\mathrm{1}}{\displaystyle \frac{e^{-j\mathit{\kappa }{r}^{\prime }}}{r^{\prime }}}\\ & \left[Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(o)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })+Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(e)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\right]\end{array}\end{array}$$

A comparison of the orthogonal expansions Eq. (B1) and Eq. (B3) leads to the desired result

$$\begin{array}{}\text{(B4)}& {\displaystyle }{a}_{nm}^{\text{inc}}=A_{\mathrm{0}}\mathrm{4}\mathit{\pi }{j}^n{Y}_{nm}^{\text{(o)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\text{(B5)}& {\displaystyle }{b}_{nm}^{\text{inc}}=A_{\mathrm{0}}\mathrm{4}\mathit{\pi }{j}^n{Y}_{nm}^{\text{(e)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\end{array}$$

with $\widehat{n}={\widehat{r}}^{\prime }$. For the incident plane wave used in this paper we have to set $b_{n,m}^{\text{inc}}\equiv \mathrm{0}$ ($a_{n,m}^{\text{inc}}\equiv \mathrm{0}$) for the aperture in a acoustically soft (hard) infinite plane.

Appendix C: Spherical-multipole expansion of a uniform complex-source beam in the presence of a plane

A complex-source beam is obtained by simply extending the real-valued coordinate r^′ where a point source is located to the complex domain

$$\begin{array}{}\text{(C1)}& {\mathit{r}}_c=\mathit{r}{}^{\prime }-j{\mathit{r}}_b\end{array}$$

As has been shown, the outwardly travelling field of the point source then turns into a complex-source beam which starts at r^′ and is travelling in the direction of r_b. Nearby the axis of propagation the CSB approximates half of a Gaussian beam with a waist centered at r^′ and a Rayleigh length of r_b. Similarly, an approach for an inwardly travelling field of a point sink leads to the other half of the Gaussian beam. Consequently, a superposition of outwardly and inwardly travelling CSBs then approximates a complete Gaussian beam. In contrast to a single CSB the superposition is regular also in the waist and in this paper referred to as a uniform CSB. Note that a uniform CSB contains also other field parts travelling in the opposite direction which however are usually of negligibly small amplitude.

In closed form a uniform CSB can be expressed as

$$\begin{array}{}\text{(C2)}& \begin{array}{rl}{\mathit{\psi }}^{\text{inc}}\left(\mathit{r}\right)& =B_{\mathrm{0}}\left[{\displaystyle \frac{e^{j\mathit{\kappa }\mathrm{|}\mathit{r}-{\mathit{r}}_c\mathrm{|}}}{\mathit{\kappa }\mathrm{|}\mathit{r}-{\mathit{r}}_c\mathrm{|}}}-{\displaystyle \frac{e^{-j\mathit{\kappa }\mathrm{|}\mathit{r}-{\mathit{r}}_c\mathrm{|}}}{\mathit{\kappa }\mathrm{|}\mathit{r}-{\mathit{r}}_c\mathrm{|}}}\right]\\ & ={\displaystyle \frac{B_{\mathrm{0}}}{\mathrm{2}j}}{\displaystyle \frac{\sin (\mathit{\kappa }\mathrm{|}\mathit{r}-{\mathit{r}}_c\mathrm{|})}{\mathit{\kappa }\mathrm{|}\mathit{r}-{\mathit{r}}_c\mathrm{|}}}\end{array}\end{array}$$

where the amplitude B₀ may be normalized to the constant $e^{\mathit{\kappa }{r}_b}$ to avoid huge numbers in the field amplitude. Using the identity Eq. (B2) the corresponding bilinear form reads

$$\begin{array}{}\text{(C3)}& \begin{array}{rl}& {\mathit{\psi }}^{\text{inc}}\left(\mathit{r}\right)=-\mathrm{8}\mathit{\pi }j{B}_{\mathrm{0}}\sum _{n=\mathrm{0}}^{\mathrm{\infty }}\sum _{m=\mathrm{0}}^n{j}_n\left(\mathit{\kappa }r\right)j_n\left(\mathit{\kappa }{r}_c\right)\\ & \left[Y_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(o)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })+Y_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })Y_{nm}^{\text{(e)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\right].\end{array}\end{array}$$

Thus, the multipole amplitudes of the spherical-multipole expansion

$$\begin{array}{}\text{(C4)}& {\mathit{\psi }}^{\text{inc}}=\sum _{n=\mathrm{0}}^{\mathrm{\infty }}\sum _{m=\mathrm{0}}^n{j}_n\left(\mathit{\kappa }r\right)\left[a_{nm}^{\text{inc}}{Y}_{nm}^{\text{(o)}}(\mathit{\vartheta },\mathit{\phi })+b_{nm}^{\text{inc}}{Y}_{nm}^{\text{(e)}}(\mathit{\vartheta },\mathit{\phi })\right]\end{array}$$

are given by

$$\begin{array}{}\text{(C5)}& {\displaystyle }{a}_{nm}^{\text{inc}}=-B_{\mathrm{0}}j\mathrm{8}\mathit{\pi }{j}_n\left(\mathit{\kappa }{r}_c\right)Y_{nm}^{\text{(o)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\text{(C6)}& {\displaystyle }{b}_{nm}^{\text{inc}}=-B_{\mathrm{0}}j\mathrm{8}\mathit{\pi }{j}_n\left(\mathit{\kappa }{r}_c\right)Y_{nm}^{\text{(e)}}({\mathit{\vartheta }}^{\prime },{\mathit{\phi }}^{\prime })\end{array}$$

Note that for a uniform CSB there is no need for a case distinction $r\gtrless r^{\prime }$ as it usually is necessary for a bilinear field expansions with real-valued source coordinates. Again, for the incident uniform CSB used in this paper we have to set $b_{n,m}^{\text{inc}}\equiv \mathrm{0}$ ($a_{n,m}^{\text{inc}}\equiv \mathrm{0}$) for the aperture in a acoustically soft (hard) infinite plane.