Results of the national antenna intercomparison 2017/2018 within the German Calibration Service (Deutscher Kalibrierdienst – DKD)

In an intercomparison organized within the framework of the German Calibration Service (Deutscher Kalibrierdienst – DKD), seven different calibration laboratories participated in the measurement of the antenna factor for three different antennas according to different standards. Between August 2017 and April 2018, measurements have been performed on a hybrid antenna, a logarithmic-periodic antenna and on an Open Ended Waveguide.

1 Introduction

The German Calibration Service (Deutscher Kalibrierdienst – DKD), is the association of the accredited laboratories in Germany (PTB-Mitteilungen, 2015) hosted at the Physikalisch-Technische Bundesanstalt (PTB), the German National Metrology Institute (PTB-Mitteilungen, 2015). The accredited laboratories in Germany are required to prove that they can determine the antenna factor correctly and traceable to the International System of Units (SI) including the specification of measurement uncertainties (GUM, 2008). Between August 2017 and April 2018, intercomparison measurements have been performed on a hybrid antenna (Schwarzbeck VULB 9163, 30 MHz–3 GHz), a logarithmic-periodic antenna (Schwarzbeck USLP 9142, 650 MHz–8 GHz) and on an Open Ended Waveguide (OEWG) in LA band (R22 or W430, 1.7 GHz–2.6 GHz) with the goal to determine the free-space antenna factor in 10 MHz steps. Below 1 GHz, measurements of the USLP and VULP antennas have been performed using the Standard-Site-method according to CISPR 16-1-6 (CISPR 16-1-6, 2014) with 10 m measurement distance on an open-area test site (OATS) or in a semi-anechoic chamber (SAC). Above 1 GHz, calibrations on USLP and VULB antennas have been performed at 3 m measurement distance in vertical or diagonal polarization according to IEEE 149 (ANSI/IEEE 149-1979, 2002), CISPR 16-1-6 (CISPR 16-1-6, 2014), ANSI C63.5 (ANSI C63.5, 2017) or to an in-house method. Additionally, single laboratories have measured VULP, USLP and OEWG antennas in 1 m distance with antenna tip as reference point according to SAE ARP 958D (SAE ARP958D, 2003).

The results, which have been documented in the DKD report DKD-V 2.5 (DKD-V 2.5, 2018), show good agreement within the specified measurement uncertainties, which seem to be realistic. While some laboratories consider variation of the phase center position for antenna factor calculation, other laboratories foresee an additional contribution to measurement uncertainty, only. However, the systematic errors introduced by this have only a minor effect on the validity of the intercomparison.

2 Intercomparison

During the 42nd meeting of the DKD technical committee “High Frequency and Optics” on 16 May 2018 in Braunschweig, it was decided to initiate an antenna factor intercomparison for all interested laboratories between August 2017 and April 2018 organized by PTB.

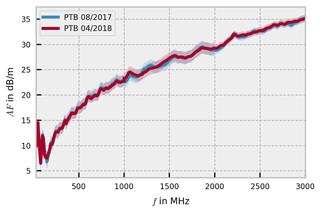
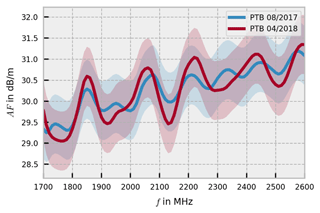
Figure 1 Free-space antenna factor of the Schwarzbeck VULB 9163 measured at PTB at the beginning and at the end of the intercomparison.

2.1 Participants

In addition to PTB, six accredited and non-accredited laboratories participated in the intercomparison: AMETEK CTS Europe GmbH in Berlin, Bureau Veritas Consumer Products Services Germany GmbH in Nürnberg, EMCCons DR. RAŠEK GmbH & Co. KG in Unterleinleiter, Obering. Berg & Lukowiak GmbH in Hüllhorst, Schwarzbeck Mess-Elektronik OHG in Schönau and Rohde & Schwarz Messgerätebau GmbH in Memmingen. To guarantee anonymity, the ordering of laboratories does not correspond to the numbering of laboratories in the results section.

2.2 Measurands

The frequency and direction dependent free-space antenna factor is defined as ratio of electric field strength $\left|E\right|$ and feeding-point voltage U_R at a reference impedance of R=50Ω:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathrm{AF}={\displaystyle \frac{\left|E\right|}{U_R}},\mathrm{with}R=\mathrm{50}\mathrm{\Omega }.\end{array}$$

For measurement of the free-space antenna factor, different measurement methods have been established depending on frequency range and measurement site. Usual methods are the Standard Site Method (SSM), the Standard Antenna Method (SAM) and the Three Antenna Method. As all methods claim traceability for the free-space antenna factor, results from different methods should be consistent which will be tested in this intercomparison.

The 1 m antenna factor according to SAE ARP 958D (SAE ARP958D, 2003) is based on Eq. (1) as well but uses the transmission measurement between two equal antennas (two antenna method) with 1 m distance between the tips and the Friis formula (Gustrau, 2013) without further correction. Therefore, the determined antenna factor is not comparable with the free-space antenna factor determined with the other methods denoted here.

Figure 2 Measurements of lab 1 for the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b). Measurement 1a according to ANSI C63.5 (10 m). Measurement 1b according to CISPR 16-1-6 (10 m).

2.3 Travelling standards

For the intercomparison, three different antennas have been used as travelling standards. For the frequency range 30 MHz–3 GHz, a hybrid antenna (Schwarzbeck VULB 9163, see VULB, 2018) with N(f) connector has been provided by the manufacturer. For the frequency range 650 MHz–8 GHz, a logarithmic-periodic antenna (Schwarzbeck USLP 9142, see USLP, 2018) with N(f) connector has been provided by PTB. In addition, an Open Ended Waveguide (OEWG) in LA band (R22 or W430) with N(f) coaxial-to-waveguide transition from M. W. Microwave Corporation has been used in the frequency range 1.7GHz –2.6 GHz provided by PTB.

Figure 3 Measurements of lab 2 for the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b). Measurement 2a according to Standard-Site-Method (CISPR 16-1-6, ANSI C63.5). Measurement 2b according to Three-Antenna-Method (CISPR 16-1-6, ANSI C63.5).

2.4 Data evaluation

Consistency of the measurement results has been evaluated with the E_n criterion (Krystek, 2012; Cox, 2000). Here, the difference between a measurement value x_i and a reference value CRV (Comparison Reference Value) will be calculated.

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }{\mathrm{DoE}}_i=x_i-\mathrm{CRV}\end{array}$$

This difference is denoted as Degree of Equivalence (DoE_i). The reference value CRV is determined as weighted mean of all N measurements of the different laboratories in such a way that the laboratories contribute according to their measurement capabilities. Results with lower specified standard measurement uncertainty u(x_i) contribute stronger as represented by a higher weighting factor w_i:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }\mathrm{CRV}=\sum _{i=\mathrm{1}}^N{w}_i\cdot x_i,\mathrm{with}{w}_i={\displaystyle \frac{\mathrm{1}}{u^{\mathrm{2}}\left(x_i\right)}}\cdot {\left(\sum _{j=\mathrm{1}}^N{\displaystyle \frac{\mathrm{1}}{u^{\mathrm{2}}\left(x_j\right)}}\right)}^{-\mathrm{1}}.\end{array}$$

Provided that the measurement results are statistically independent, according to the “Guide to the expression of uncertainty in measurement” (GUM, 2008), it follows for the uncertainty u(CRV) of the Comparison Reference Value:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }{u}^{\mathrm{2}}\left(\mathrm{CRV}\right)=\sum _{i=\mathrm{1}}^N{w}_i^{\mathrm{2}}\cdot u^{\mathrm{2}}\left(x_i\right).\end{array}$$

Normalizing the DoE_i to the corresponding expanded measurement uncertainty U(DoE_i) (which in case of a sufficiently high effective degree of freedom corresponds to twice the standard measurement uncertainty for a confidence interval of 95 %) results in the E_ni value, which is a measure for the conformity of the individual measurement with the Comparison Reference Value:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }{E}_{ni}={\displaystyle \frac{{\mathrm{DoE}}_i}{U\left({\mathrm{DoE}}_i\right)}}.\end{array}$$

As long as the participating laboratories estimate their measurement uncertainties realistically, the E_ni absolute value is below one in 95 % of all cases. Considering the strong covariance between measurement value x_i and reference value CRV (as the measurement value was used to calculate the reference value), the following equation can be used to calculate the E_ni value:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{E}_{ni}={\displaystyle \frac{x_i-\mathrm{CRV}}{\sqrt{U^{\mathrm{2}}\left(x_i\right)-U^{\mathrm{2}}\left(\mathrm{CRV}\right)}}}.\end{array}$$

Note that due to the correlation of single measurement value and Comparison Reference Value U²(CRV) has to be substracted in the square root of the denominator. In one case, the measurements of a single laboratory did not contribute to the CRV as there was a constant offset compared to the other laboratories over frequency. In this case x_i and CRV are not correlated and E_ni is calculated according to:

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{E}_{ni}={\displaystyle \frac{x_i-\mathrm{CRV}}{\sqrt{U^{\mathrm{2}}\left(x_i\right)+U^{\mathrm{2}}\left(\mathrm{CRV}\right)}}}.\end{array}$$

As usual in antenna technology, all measurements including measurement uncertainty are decibel.

Figure 4 Measurements of lab 3 for the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b).

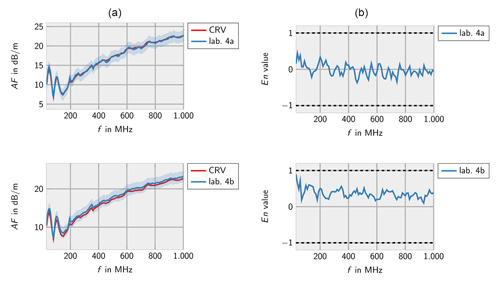
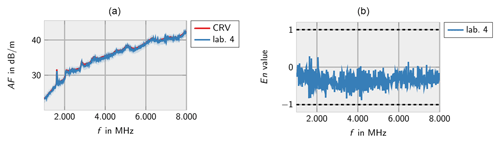
Figure 5 Measurements of lab 4 for the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b). Measurement 4a according to ANSI C63.5 (10 m). Measurement 4b according to ANSI C63.5 (3 m).

Figure 6 Measurements of lab 5 for the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b).

Figure 7 Measurements of lab 6 for the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b).

Figure 8 Measurements of lab 7 for the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b).

3 Results

3.1 Free-space antenna factor

3.1.1 Hybrid antenna (30 MHz–3 GHz)

Figure 1 shows the results of the antenna factor measurements at PTB for the hybrid antenna Schwarzbeck VULB 9163 at the beginning and the end of the intercomparison. The results are consistent within the specified measurement uncertainty, indicating that the antenna properties did not change during the intercomparison.

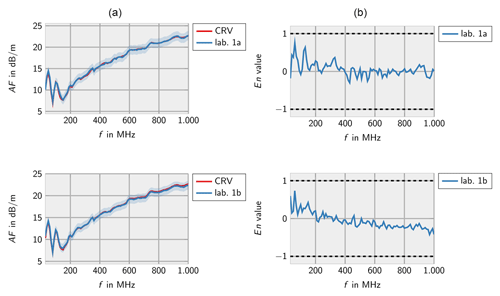
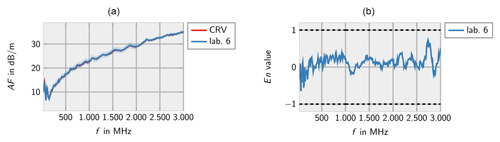
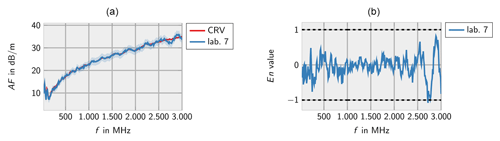
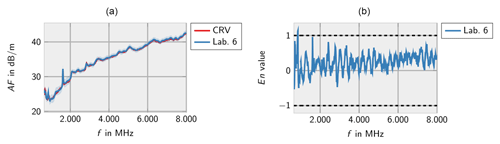
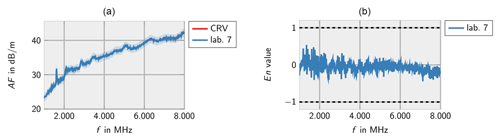
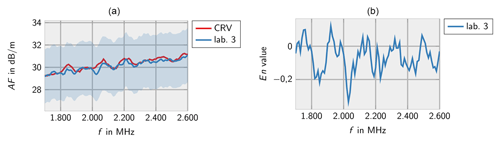
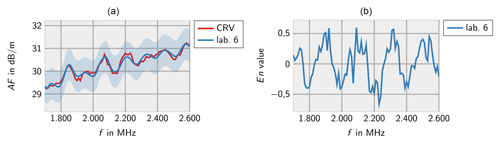
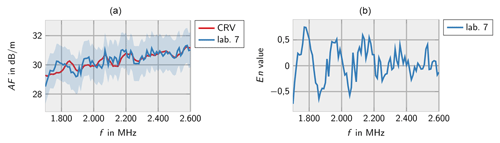
Figures 2–8 show the results of the participating laboratories. Laboratory 1 and 4 used two different methods to determine the free-space antenna factor. The measurements of lab 1 are considered to be independent. Therefore, both measurements are contributing to the CRV. Measurement 4b has been excluded from the calculation of the CRV in order not to let near-field effects due to the small measurement distance influence the CRV. In this case the E_n value has been calculated according to Eq. (7).

The decaying trend in measurement 1b shows that the antenna factor is estimated too high at lower frequencies and too low at higher frequencies. This is due to the systematic error in the CRV resulting from some laboratories considering the phase center position in their calculation, only.

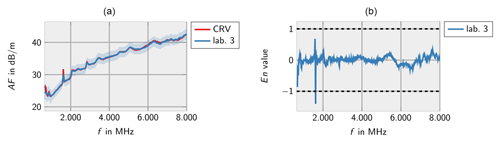
In general, the measurements of all laboratories are consistent with the CRV. Only very few deviations are identified for lab 3 at low frequencies and lab 7 at high frequencies.

3.1.2 Log. per. dipole antenna (650 MHz–8 GHz)

Figure 9 shows the results of the antenna factor measurements at PTB for the logarithmic-periodic antenna Schwarzbeck USLP 9142 at the beginning and the end of the intercomparison. The results are consistent within the specified measurement uncertainty, indicating that the antenna properties did not change during the intercomparison, as well.

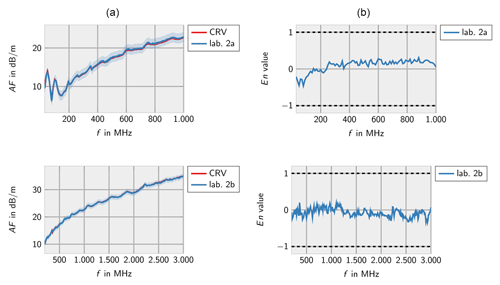
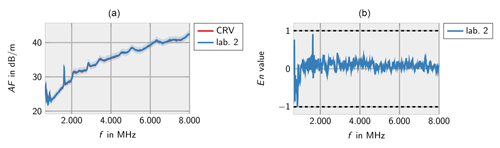
Figures 10–14 show the measurement results from the different laboratories. As before, the results indicate that the laboratories can determine the correct antenna factors within the specified measurement uncertainties independent from the measurement method. Single incompatible measurement results are found below 1000 MHz and at a peak of the antenna factor.

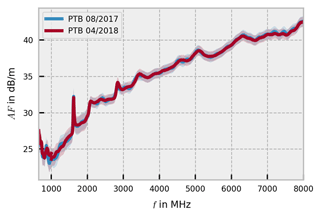
Figure 9 Free-space antenna factor of the Schwarzbeck USLP 9142 measured at PTB at the beginning and at the end of the intercomparison.

Figure 10 Measurements of lab 2 for the Schwarzbeck USLP 9142 (a) and corresponding E_n values (b).

3.1.3 Open-ended waveguide (1.7 GHz–2.6 GHz)

Figure 15 shows the results of the antenna factor measurements at PTB for the OEWG at the beginning and the end of the intercomparison. Here, the results are consistent, as well, although a better match would have been preferred.

Figure 11 Measurements of lab 3 for the Schwarzbeck USLP 9142 (a) and corresponding E_n values (b).

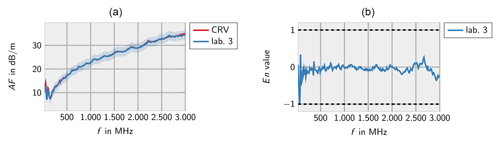
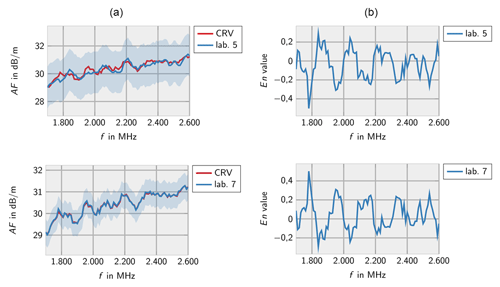
Figures 16–18 show the measurement results from the different laboratories, which are consistent as well. Unfortunately, only three laboratories measured the OEWG which restricts the informative value of the results.

Figure 12 Measurements of lab 4 for the Schwarzbeck USLP 9142 (a) and corresponding E_n values (b).

Figure 13 Measurements of lab 6 for the Schwarzbeck USLP 9142 (a) and corresponding E_n values (b).

Figure 14 Measurements of lab 7 for the Schwarzbeck USLP 9142 (a) and corresponding E_n values (b).

3.2 Antenna factor according to SAE ARP 958D

3.2.1 Hybrid antenna (30 MHz–3 GHz)

Figure 19 shows the measurement results and E_n values of the participating laboratories for the hybrid antenna Schwarzbeck VULB 9163 for the 1 m antenna factor according to SAE ARP 958D. While all reported measurements are consistent above 200 MHz, lab 4 reports inconsistent measurement values below 200 MHz and is advised to revise its measurement uncertainty budget.

Figure 15 Free-space antenna factor of the OEWG measured at PTB at the beginning and at the end of the intercomparison.

Figure 16 Measurements of lab 3 for the OEWG (a) and corresponding E_n values (b).

3.2.2 Log.-per. dipole antenna (650 MHz–8 GHz)

Figure 20 shows the measurement results and E_n values of the participating laboratories for the logarithmic-periodic antenna Schwarzbeck USLP 9142 for the 1 m antenna factor according to SAE ARP 958D. Two single incompatible measurement results in the lower frequency range can be explained by statistics.

Figure 17 Measurements of lab 6 for the OEWG (a) and corresponding E_n values (b).

Figure 18 Measurements of lab 7 for the OEWG (a) and corresponding E_n values (b).

3.2.3 Open-ended waveguide (1.7 GHz–2.6 GHz)

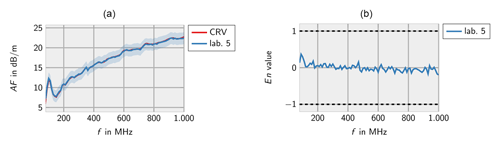
Figure 21 shows the measurement results and E_n values of the laboratories 5 and 7 for the OEWG for the 1 m antenna factor according to SAE ARP 958D. The measurement results are consistent, however, the informative value is restricted due to two participants, only.

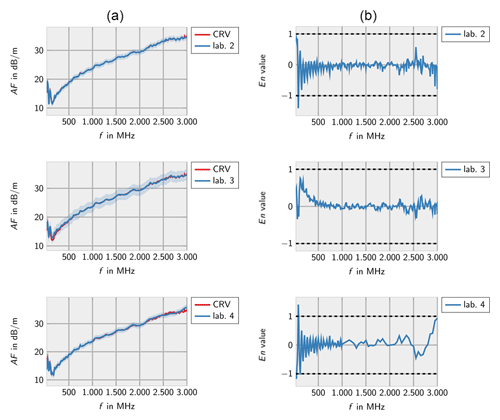
Figure 19 Measurements of lab 2–4 for the 1 m antenna factor according to SAE ARP 958D of the Schwarzbeck VULB 9163 (a) and corresponding E_n values (b).

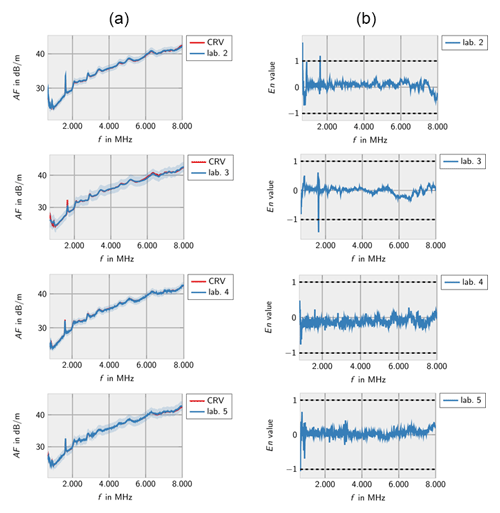
Figure 20 Measurements of lab 2–5 for the 1 m antenna factor according to SAE ARP 958D of the Schwarzbeck USLP 9142 (a) and corresponding E_n values (b).

Figure 21 Measurements of lab 5 and 7 for the 1 m antenna factor according to SAE ARP 958D of the OEWG (a) and corresponding E_n values (b).

4 Conclusions

The results of the intercomparison are very satisfactory. All laboratories estimate their measurement uncertainty in a realistic way. Only one laboratory should reconsider its measurement uncertainty budget in the lower frequency range. The results obtained for the free-space antenna factor according to the standards IEEE 149, CISPR 16-1-6 and ANSI C63.5 are comparable independent from the method used.

A problem is that some laboratories are considering the position of the phase center in their antenna factor calculation while others do not. This leads to a systematic error of the CRV. While the E_n value is estimated too large for laboratories that consider the phase center, it is too small for those who do not. Therefore, the comparability of the CRV obtained here to antenna factors determined using near-field methods is restricted.