Dynamic Eigenimage Based Background and Clutter Suppression for Ultra Short-Range Radar
Matthias G. Ehrnsperger
Maximilian Noll
Stefan Punzet
Uwe Siart
Thomas F. Eibert
Background and clutter suppression techniques are important towards the successful application of radar in complex environments. We investigate eigenimage based methodologies such as principal component analysis (PCA) and apply it to frequency modulated continuous wave (FMCW) radar. The designed dynamic principal component analysis (dPCA) algorithm dynamically adjusts the number of eigenimages that are utilised for the processing of the signal. Furthermore, the algorithm adapts towards the number of objects in the field of view as well as the estimated distances. For the experimental evaluation, the dPCA algorithm is implemented in a multi-static FMCW radar prototype that operates in the K-band at 24 GHz. With this background and clutter removal method, it is possible to increase the signal-to-clutter-ratio (SCR) by 4.9 dB compared to standard PCA with mean removal (MR).
- Article
(2439 KB) - Full-text XML
- BibTeX
- EndNote
Radar systems have become very small in size due to vast technological developments. They are found in various user electronics applications such as cellphones and smartwatches, as well as in the automotive sector where they are utilised, e.g., for advanced driver assistance systems. In these applications, radar systems are employed for motion and proximity detection as well as for gesture recognition. The commonly known passive infrared (PIR) sensors have been established devices for motion and proximity detection for many decades (Budzier and Gerlach, 2011, pp. 5). They are still used today in many private households to switch the lighting of front doors. PIR sensors, however, are not very adaptable and insensitive, so that they are increasingly being displaced from the market. Especially there, where people are in dangerous environments, the credo is safety first. In order to protect life it is vital to guarantee a maximum detection performance. It is important to maintain this detection performance regardless of the installation situation and environment. The installation situations can be unfavourable, e.g., outdoors, and may include the appearance of signal degrading sediments on the sensors (Ehrnsperger et al., 2019). The system may be operated within strongly echoic environments, e.g., between the street and the bottom of a vehicle or in hallways. In such environments the radar system would be exposed to bright clutter, which may deteriorate the object detection probability Another factor that affects the object detection probability are the antennas. The employed antennas might be of low directivity, or be placed close to each other. The latter favours mutual coupling which may reduce the detection probability of living objects even further. The radar system itself may be mobile and employed in various environments. In each of those environments the radar system has to ensure safety and detect objects reliably.
Radar based safety systems in the context of this work are mostly designed to cover ranges below 10 m. These so-called ultra short-range radars are subject to multi-target detection tasks, dynamic clutter, and environmental influences. All of these circumstances must be taken into consideration to maintain a sufficient probability of detection and probability of false alarms. Consequently, clutter and background suppression is very relevant and crucial to achieve this goal. Several approaches and methods to remove clutter and background are presented in literature. Kim et al. (2007) investigate predictive deconvolution with filtering in the wavenumber domain. Furthermore, Kim et al. (2007) investigate filtering by Radon transform and f−k filtering, which is consecutively compared with singular value decomposition (SVD)-based eigenimage filtering for ground penetrating radar (GPR). Also, for GPR, Khan and Al-Nuaimy (2010) investigate mean subtraction and SVD to suppress background signals. Mathematically more complex learning algorithms such as independent component analysis (ICA) are evaluated in Sharma et al. (2017). The methods are further compared to subtraction methods like median and mean subtraction. Matched filtering is investigated by Strange et al. (2002). This matched filter, however, is limited to detection of single objects. However, in numerous applications and classification tasks it is desirable to detect more than one object at a time. A phasor offset compensation method for static clutter removal is proposed in Xiong et al. (2017). SVD is compared to frame differencing (FD) in Eren et al. (2017) and Abujarad et al. (2005). In Ehrnsperger et al. (2021) standard as well as modified eigenvalue filtering methods are experimentally evaluated. Sophisticated machine learning algorithms for clutter removal and classification are presented in Ma et al. (2020) and Ehrnsperger et al. (2020b). Taking the available literature into consideration, our investigations focus on clutter and background removal by employing eigenvalue decomposition (EVD) in combination with principal component analysis (PCA) as basis. In particular, we investigate how the reconstruction of a measured signal can be completed dynamically to remove background and clutter, but also maintaining a sufficient detection probability for low-velocity objects. This dynamic principal component analysis (dPCA) reconstruction approach is firstly implemented and evaluated in a simulative environment. Subsequently, a compact 24 GHz radar prototype is set up to conduct measurements in real life scenarios. Finally, the approach is compared with standard procedures in terms of performance and implementability.
A primary goal of this paper is to determine, whether dPCA is suitable to remove background and clutter from USRR systems in echoic environments. Is dPCA able, in combination with a suitable mean removal method, to detect low-velocity and temporarily static targets in bright clutter environments? Which mean removal method is required and why? How well can dPCA suppress background and clutter and how well does it work compared to basic PCA? Is the proposed dPCA approach operational in combination with experimentally acquired radar signals? How long does it take to compute the dPCA and the complete signal processing chain?
In Sect. 2, the employed background and clutter suppression methodology is introduced. The results are summarised and discussed in Sect. 3, before the conclusions are drawn in Sect. 4.
In bright clutter environments, the signal that is scattered by the actual to-be-detected targets is hardly detectable.
2.1 Data and Noise Subspaces
By utilising (EVD), it is possible to split a square data matrix into subspace matrices. The most prominent eigenvalues result from environmental clutter and only a minor part is due to system noise. When only two subspaces are used (noise and data), the clutter is part of the data matrix and cannot be removed (Sabushimike et al., 2016; Shehab et al., 2019). Considering additive noise, a measured frame of a radar system Ameas is an M×N matrix, where N is the number of chirps and M is the number of time-steps. This matrix can be decomposed into
We assume that clutter represents the dominant part of the signal and so it is captured within the first few principal components PRCs. The PRCs are calculated by the PCA and contain the information that is required to reconstruct the initial signal. We assume that the PRCs contain most information about the signal. In contrast to the minor components MICs, which are the eigenvectors corresponding to the smallest eigenvalues. This leads to the representation (Xiaoming et al., 2016)
where qi∈ℝn are the eigenvectors of the data matrix A. We assume the clutter is contained in q−1 PRCs while the noise is contained in n−p MICs of the dataset. The clutter- and noise-free data is then obtainable by summing up the corresponding eigenimages
where . The values for the lower and upper bounds of the eigenvalues, q and p, are set with respect to the data matrix. Since it can be assumed that most of the clutter is present in the first eigenvalue, it is mostly sufficient for naïve clutter removal to set q=2 (Jorgensen and Hansen, 2012). The same applies for p, in naïve background and clutter removal approaches, p can be simply set to the number of chirps that has been chosen for a frame, e.g., 32. In our extended approach, both values, p and q, are set dynamically, dependent on the measured signals. As we assume that Afilt is clutter-free and noise-free, the matrix only contains the signal that has been scattered by the to-be-detected target or targets. The clutter and noise is best suppressed with an adequate choice of q and p, in combination with interframe mean removal (IMR). Then, it is possible to detect both moving and temporarily static targets, as presented throughout the next sections. Please note that a given data matrix X does not have to be a square matrix and has the dimensions of M×N in the following. This is possible since the PCA calculates the eigenvalues via the correlation matrix R, this correlation matrix is a square matrix (Wold et al., 1987). Furthermore, the data matrix X and the subspace matrices A are real valued, in both simulations and measurements, since the employed radar system only allows to obtain the in-phase part of the received signal.
2.2 Principal Component Analysis (PCA)
The PCA is a widely used statistical method that is employed, e.g., for data reduction, classification of signals, and prediction in regression models (Wold et al., 1987; Jolliffe, 2002). In our application, however, we employ the PCA to remove clutter and noise. In general, PCA can be seen as an eigenvector-based multivariate data analysis method. Here, PCA moves the data X to a new coordinate system by using an orthogonal transformation. This new coordinate system is spanned by the PRCs. The PRCs are selected in a way that they are mutually uncorrelated. This is accomplished by so-called PCA whitening (Friedman, 1987; Kessy et al., 2018). It means that the total variance of the received signal X is distributed over all PRCs. So, the combination of the variances of all PRCs is the variance of the initial received signal X. We assume that the first PRC contains most of the variance of X, the second PRCs contains the second most variance of X, and so on. For our multistatic radar system, the data is arranged in a way that the N chirps are placed along the rows, and the M samples of each chirp are placed along the columns of X. The largest variance in the data generates the most significant pattern in the eventual range-Doppler map (RDM) (Kabourek et al., 2012). In our context, this is the clutter. The smallest variance is represented by the noise in the data and corresponds to the smallest PRCs, the so-called MICs (Kong et al., 2017). Therefore, by filtering the first PRCs and the MICs, clutter and noise can be suppressed. The suggested approach is as follows. In the first step the mean value is subtracted from the dataset,
Then the eigenvectors of the square matrix are used to build the transformation matrix and calculate the projected data
where and . For clutter and noise reduction the data is reconstructed with only a few PRCs. The filtered reconstruction can be written as
where y∈ℝM and w∈ℝN. For the second method, is replaced in Eqs. (4) and (5) by a different mean removal method. We named this method interframe mean removal (IMR) in the following, according to
since it includes information about previous frames. This helps to prevent the undesired suppression of low-velocity objects. Here, depending on the current timestep i>0 and the corresponding data matrix X(i), IMR is calculated as
2.3 Dynamic PCA (dPCA) Reconstruction
The first step of the dPCA approach is performed with an IMR process of the measurement in order to be able to detect temporary-static targets. When considering a moving target, it is reasonable to exclude the first PRC from the reconstruction. If the target is in a temporarily static state, however, this removal suppresses the target and makes it invisible. Therefore, the lower boundary of the eigenvalues q has to be chosen dynamically. Additionally, the upper boundary p has to be chosen dynamically to reduce the noise level. In order to define these reconstruction boundaries, p and q, of the dPCA, our algorithm firstly calculates the eigenvalues λ. Then the eigenvalue ratio
is calculated. Here, the first eigenvalue is related to the sum of all other eigenvalues. In Fig. 1 the trends of the ratio r are plotted for the raw data, the mean removal (MR) data, and the IMR data. The ratio for the first eigenvalue is considerably large, relative to the raw data. This is also the case for IMR, where the first few eigenvalues are considerably large. After conducting a simple MR to the raw data, the course of the ratio becomes flat. Throughout the experimental evaluation of the eigenvalues a decision threshold has been defined empirically. This decision threshold decides whether or not the first eigenvalue is included into the reconstruction as the lower boundary
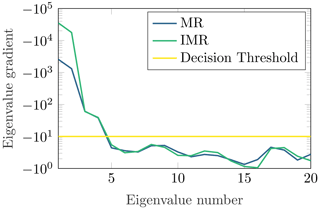
By doing so, the undesired side effect of suppressing low-velocity objects can be prevented. To define the total number of eigenvalues that are included into the reconstruction, also the upper boundary p is chosen dynamically. Hereby, the gradient of the eigenvalues, as illustrated in Fig. 2, is calculated. Here, also an empirically evaluated decision threshold is set to −10. That means the upper boundary p includes all eigenvalues that have a gradient of below −10. We further implement an IMR, where the current mean is combined with a previous mean value that fades exponentially.
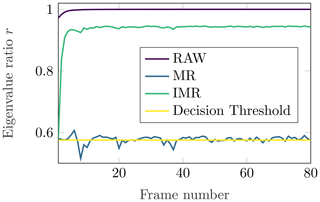
Figure 1Development of the ratio r of the eigenvalues according to Eq. (9) for 80 frames of one measurement series. Each frame consists of an M×N matrix (here, 256 time-steps × 32 chirps).
2.4 Simulative and Experimental Setup
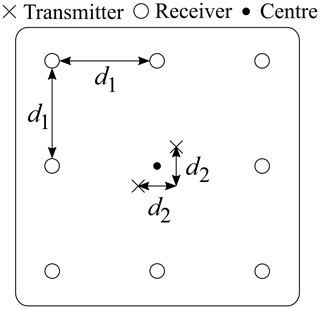
The dPCA as well as the standard PCA are employed in combination with a cell averaging constant false alarm rate (CA-CFAR) that handles the final detection of the objects. After implementing and testing the dPCA in a simulative environment, the method is now applied in real-life measurements. In the following, the hardware shown in Figs. 3 and 4 is in focus. Here, primarily the INRAS “Radarbook” K-Band radar system is employed, see Fig. 4. The Radarbook is a commercial rapid prototyping system with a modified frontend for our application (Inras GmbH, 2020). In order to maximise the coverage area of the radar system, omnidirectional eddy current suppressing (ECS) monopole antennas are employed for all channels (transmit as well as receiving). The transmitting channels are placed in the centre of the groundpad, the receiving channels are placed at the edges of the board, see Fig. 3.
2.5 Quality Evaluation Method
For the final evaluation of the filters, it is necessary to qualify them quantitatively. Therefore, the whole basis of this evaluation-tool, the so-called signal-to-clutter-ratio (SCR), is presented in the following. Analogous to the signal-to-noise-ratio (SNR), the SCR is the ratio of the signal power to the clutter power In a simulative environment it is rather simple to separate signal- and clutter-subspaces. For measurements in highly reflective environments, however, this becomes much more complex, so an approximation is necessary. The following approach is empirical and has grown throughout this work. It is based on analysing the RDMs that are calculated for each frame.
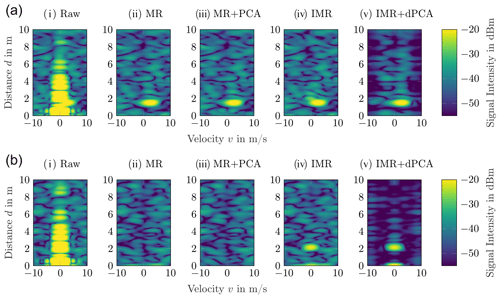
Figure 5(a) Measurement of a moving living object. All data is from the same single channel of the radar system. All of the investigated background removal methods can detect the person. The best results for background and clutter removal is obtained with IMR + dPCA. The dPCA starts hereby with the second eigenimage. (b) Measurement of a living object at rest. Standard MR and PCA fail to detect the object. With IMR + dPCA it is still possible to detect the object as the reconstruction of the dPCA includes the first eigenimage. As the first eigenimage is employed in (v), unsuppressed clutter remains at zero distance and zero velocity. Experimental investigation of the proposed clutter and background removal techniques in combination with the presented mean removal approaches.
First, the RDM is analysed to detect a possible target. This can be performed with different approaches, for example by hand, with a certain threshold level, or by a 2D-CA-CFAR approach. The result of each variant should be the same: information about the cells that contain the required signal which is scattered by the to-be-detected object. The RDM values of the corresponding target location are then utilised to estimate the signal power. We assume that the RDM is a matrix and R(m,n) is the RDM value at position (m,n). The positions of the detected cells (k,l) are stored in the quantity . Then, the estimated signal power can be calculated by
where d is the amount of elements in D, which, on the other hand, is the number of detected cells. The estimation of the clutter (or more general, the background) power
can be performed similarly; here, all cells except the ones included in D are utilised. Consequently, our employed quality evaluation-tool is the SCR, defined by
This method is independent of an exact separation of signal and clutter. Therefore, it can be easily performed on any RDM in either a simulated or real world environment.
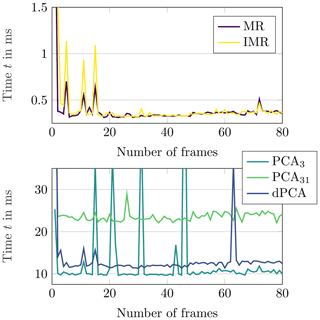
Figure 6Overview of the required computation times for all considered filter methods over a period of 80 successive frames. For a better overview, MR and IMR are illustrated with a smaller time axis in the upper plot. The indices of the PCA represent the number of eigenimages that are employed for the reconstruction, i.e., PCA31 includes 31 eigenimages and requires more time for the computation than PCA3 with 3 eigenimages.
For experimental evaluation, we conducted measurements in a multi-reflective narrow hallway. Multiple motion profiles with one or more objects are investigated. For convenience only the RDMs of one single channel of the radar system are illustrated in Fig. 5a and b.
In Fig. 5a, a person is walking towards the USRR from a distance of about 1.8 m. In Fig. 5b, the same person is at a distance of 2.2 m and stopped walking. The RDM from the raw data contains bright static clutter which is caused by the mutual coupling of the antennas and by the reflective environment. The information about the velocity and distance of the living object is contained in the measurement, however, the CA-CFAR is only able to extract this information if the background and clutter removal techniques are employed. If merely the mean is removed in Fig. 5a, either with (ii) MR or (iv) IMR, the object is already distinguishable from clutter and noise. By combining (iii) MR + PCA, the noise level cannot be reduced further. However, if (v) IMR + dPCA are combined the SCR can be increased by 4.9 dB.
Table 1Quantitative comparison of the different methods. By combining IMR + dPCA the best SCR values and most resilient results can be obtained. Additionally, IMR + dPCA can be calculated 0.2 ms faster than MR + PCA. n/a: not applicable
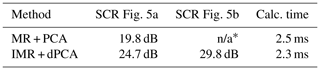
* Utilising MR + PCA cancelled out the object for this measurement.
Employing the same signal processing chain for Fig. 5b, the object vanishes for (ii) MR and (iii) PCA. In a safety critical application this behaviour can lead to extremely dangerous situations and is unacceptable. The (iv) IMR maintains the static object with an SCR of 20.4 dB. If then the (v) dPCA is applied the SCR increases by 9.4 to 29.8 dB. The quantitative values of the results are stated in Table 1. The performance of the discussed methods is not only dependent on the obtainable SCR. In addition to this ratio, the computation time, which is required for the calculations, has to be investigated. Therefore, the tracked computation time during an evaluation of 80 frames is displayed in Fig. 6. The computation time has been evaluated on one single core of the central processing unit (CPU) with maximum priority1. The peaks are outliers which are caused by the operating system.
Eigenvector-based multivariate data analysis methods, such as PCA and dPCA, are helpful tools to suppress static and dynamic clutter from USRR measurements. By adaptively choosing the eigenvalues that are utilised for the reconstruction, the detection performance is increased and adjusted to changing environments. The performance can be further increased by including inter-frame information in the mean-removal process. By doing so it is possible to avoid the undesired suppression of low-velocity objects. The proposed dPCA method outperforms the standard PCA. The empirically and experimentally evaluated numbers of PRCs and MICs that are employed for the reconstruction, as well as the defined decision threshold values are reasonable and meaningful for the employed radar hardware. To employ the dPCA in varying environments as well as in combination with different radar systems, these values can be adjusted easily and efficiently. In order to further extend the detection performance, it is reasonable to implement methodologies from the field of machine learning (ML) (Ehrnsperger et al., 2020a).
The underlying research data can be requested from the authors.
MGE and MN conceived the presented idea. MN and MGE implemented the model and performed the computations. MN and MGE verified the analytical methods. MN and MGE carried out the experiments. MGE wrote the manuscript in consultation with MN, SP, US and TFE. TFE supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Kleinheubacher Berichte 2020”.
This paper was edited by Romanus Dyczij-Edlinger and reviewed by Adrian Amor-Martin and one anonymous referee.
Abujarad, F., Nadim, G., and Omar, A.: Clutter Reduction and Detection of Landmine Objects in Ground Penetrating Radar Data Using Singular Value Decomposition (SVD), in: IEEE Proceedings of the 3rd International Workshop on Advanced Ground Penetrating Radar, https://doi.org/10.1109/agpr.2005.1487840, 2005. a
Budzier, H. and Gerlach, G.: Thermal Infrared Sensors: Theory, Optimisation and Practice, John Wiley & Sons, Ltd, https://doi.org/10.1002/9780470976913, 2011. a
Ehrnsperger, M. G., Siart, U., Moosbühler, M., Daporta, E., and Eibert, T. F.: Signal degradation through sediments on safety-critical radar sensors, Adv. Radio Sci., 17, 91–100, https://doi.org/10.5194/ars-17-91-2019, 2019. a
Ehrnsperger, M. G., Brenner, T., Hoese, H. L., Siart, U., and Eibert, T. F.: Real-Time Gesture Detection Based on Machine Learning Classification of Continuous Wave Radar Signals, IEEE Sens. J., 21, 8310–8322, https://doi.org/10.1109/JSEN.2020.3045616, 2020a. a
Ehrnsperger, M. G., Brenner, T., Siart, U., and Eibert, T. F.: Real-Time Gesture Recognition with Shallow Convolutional Neural Networks Employing an Ultra Low Cost Radar System, German Microwave Conference, Cottbus, 9–11 March 2020, Germany, 2020b. a
Ehrnsperger, M. G., Noll, M., Siart, U., and Eibert, T. F.: Background and Clutter Removal Techniques for Ultra Short Range Radar, in: 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021, 78–81, available at: https://ieeexplore.ieee.org/document/9337322, last access: 30 April 2021. a
Eren, C., Karamzadeh, S., Caliskan, A., Orhan, M., and Çilesiz, I.: Background Subtraction Techniques to Detect Human Vital Signs Using UWB GPR, in: International Conference on Advanced Technology and Sciences, 9–12 May 2017, 743–747, available at: https://bit.ly/bsttdhvsuuwbGPR (last access: 17 July 2019), 2017. a
Friedman, J. H.: Exploratory Projection Pursuit, J. Am. Stat. Assoc., 82, 249–266, https://doi.org/10.1080/01621459.1987.10478427, 1987. a
Inras GmbH: Inras Radarbook, http://www.inras.at/produkte/radarbook.html, last access: 21 July 2020. a
Jolliffe, I. T.: Principal Component Analysis, Springer-Verlag, https://doi.org/10.1007/b98835, 2002. a
Jorgensen, K. W. and Hansen, L. K.: Model Selection for Gaussian Kernel PCA Denoising, IEEE T. Neur. Net. Lear., 23, 163–168, https://doi.org/10.1109/tnnls.2011.2178325, 2012. a
Kabourek, V., Černý, P., and Mazanek, M.: Clutter Reduction Based on Principal Component Analysis Technique for Hidden Objects Detection, Radioengineering, 21, 464–470, https://dspace.vutbr.cz/handle/11012/37067, 2012. a
Kessy, A., Lewin, A., and Strimmer, K.: Optimal Whitening and Decorrelation, The American Statistician, 72, 309–314, https://doi.org/10.1080/00031305.2016.1277159, 2018. a
Khan, U. S. and Al-Nuaimy, W.: Background Removal from GPR Data Using Eigenvalues, in: Proceedings of the XIII Internarional Conference on Ground Penetrating Radar, Lecce, Italy, 21–25 June 2010, 1–5, https://doi.org/10.1109/icgpr.2010.5550079, 2010. a
Kim, J.-H., Cho, S.-J., and Yi, M.-J.: Removal of Ringing Noise in GPR Data by Signal Processing, Geosci. J., 11, 75–81, https://doi.org/10.1007/BF02910382, 2007. a, b
Kong, X., Hu, C., and Duan, Z.: Principal Component Analysis Networks and Algorithms, Springer-Verlag GmbH, available at: https://www.ebook.de/de/product/28369174/xiangyu_kong_changhua_hu_zhansheng_duan_principal_component_analysis_networks_and_algorithms.html (last access: 9 January 2020), 2017. a
Ma, L., Wu, J., Zhang, J., Wu, Z., Jeon, G., Zhang, Y., and Wu, T.: Research on Sea Clutter Reflectivity Using Deep Learning Model in Industry 4.0, IEEE T. Ind. Inform., 16, 5929–5937, https://doi.org/10.1109/TII.2019.2957379, 2020. a
Sabushimike, D., Na, S., Kim, J., Bui, N., Seo, K., and Kim, G.: Low-Rank Matrix Recovery Approach for Clutter Rejection in Real-Time IR-UWB Radar-Based Moving Target Detection, Sensors, 16, 1409, https://doi.org/10.3390/s16091409, 2016. a
Sharma, P., Kumar, B., Singh, D., and Gaba, S. P.: Critical Analysis of Background Subtraction Techniques on Real GPR Data, Defence Sci. J., 67, 559, https://doi.org/10.14429/dsj.67.10048, 2017. a
Shehab, M. A., Obaidi, M. A. S. A., Hos, I., and Karamzadeh, S.: Subspace Clutter Removal Techniques in GPR Images, Progress In Electromagnetics Research M, 82, 139–147, https://doi.org/10.2528/pierm19032511, 2019. a
Strange, A., Chandran, V., and Ralston, J.: Signal Processing to Improve Target Detection Using Ground Penetrating Radar, in: Proceedings of the 4th Australasian Workshop on Signal Processing and Applications, Brisbane, Australia, 17–18 December 2002, 139–142, available at: https://eprints.qut.edu.au/2994/ (last access: 10 March 2019), 2002. a
Wold, S., Esbensen, K., and Geladi, P.: Principal Component Analysis, Chemometr. Intell. Lab., 2, 37–52, https://doi.org/10.1016/0169-7439(87)80084-9, 1987. a, b
Xiaoming, Z., Jian, T., Meijun, Z., and Qunce, J.: Noise Subspaces Subtraction in SVD Based on the Difference of Variance Values, J. Vibroeng., 18, 4852–4861, https://doi.org/10.21595/jve.2016.16745, 2016. a
Xiong, Y., Chen, S., Xing, G., Peng, Z., and Zhang, W.: Static Clutter Elimination for Frequency-modulated Continuous-wave Radar Displacement Measurement Based on Phasor Offset Compensation, Electron. Lett., 53, 1491–1493, https://doi.org/10.1049/el.2017.2915, 2017. a
Intel(R) Core(TM) i9-10900K @ 3.70 GHz, Windows 10 Enterprise version 1909