Influence of LO cable movements on VNA measurements using Frequency Extensions

In this study, the impact of local oscillator cable movements or drift during VNA measurements using frequency extenders is investigated. A non-reciprocal measurement error caused by alterations of the local oscillator signal in R 900 (WR 10) waveguide measurements from 75 to 110 GHz is observed and systematically analyzed. Furthermore, the theory behind this effect and its implications on measurement results are discussed, as well as possible corrections for both calibrated and raw measurement data.

1 Introduction

In vector network analyzer (VNA) set-ups with two or more test ports, cable movements are often a significant source of measurement uncertainty (MU). When utilizing VNA frequency extenders, instead of using a VNA base unit alone, all cables connecting each extender to the VNA could be moved and are potential MU sources. In some cases, a considerable cable movement is required, e.g. in set-ups used for the characterization of large devices under tests (DUTs) or antennas. Each VNA extender is usually connected with a local oscillator (LO) cable, a radio frequency (RF) cable and two intermediate frequency (IF) cables to a VNA base unit. While LO cable movements are the primary influence on the LO signal during measurements in laboratories with stable set-ups and good environmental control, similar changes in the LO signal could also arise from temperature fluctuations or drift under less ideal conditions.

Measurement errors resulting from these cable movements, as demonstrated in Novotny (2019) and Arsenovic (2020), may be underestimated or overlooked. Often, reflection measurements are utilized to assess cable stability, yet they remain unaffected by the underlying cause, leading to not detecting and consequently neglecting the issue. When employing conventional methods to account for cable movements and evaluate measurement uncertainties, as outlined in the EURAMET Calibration Guide No. 12 (CG-12) by Zeier et al. (2018) or the METAS VNA Tools Math Reference Federal Institute of Metrology (METAS) (2024), these influences are not comprehensively addressed yet.

In this study, the impact of LO cable movement is systematically investigated. Initially, the theoretical effects of a change in the LO signal at one frequency extender is analyzed and equations for error correction to account for this effect are derived. Additionally, an experiment is conducted employing a phase shifter to methodically examine changes in the LO signal phase during measurements. The phase shifter is integrated into the LO cable path, and the phase value setting is varied from 1 to 10° while measuring the scattering parameters (S-parameters) of a thru connection using R 900 (WR 10) VNA frequency extenders from 75 to 110 GHz. This experimental set-up with a phase shifter facilitates a systematic analysis of the effects discussed by Novotny (2019) and Arsenovic (2020), establishing a connection to theoretical considerations.

2 Theoretical impact of cable movements

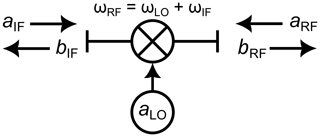
An ideal RF mixer, as depicted in Fig. 1, can be described by a simple S-parameter matrix according to Willliams et al. (2005). Therefore, the incident wave a_RF can be related to the outgoing wave b_IF by a factor a_LO, which depends on the phase of the LO signal at the mixer input

$$\begin{array}{}\text{(1)}& b_{\text{IF}}=a_{\text{LO}}\cdot a_{\text{RF}}.\end{array}$$

Most commonly, mixers are operated in saturation. Therefore, a change in the amplitude of the LO signal has a minor effect on the output signal, and the factor a_LO describes only a change in the LO signal phase. In this work the effect of the LO signal amplitude change due to the cable movement will be neglected ($\left|a_{\text{LO}}\right|=\mathrm{1}$).

Figure 1 Ideal RF Mixer as described by Willliams et al. (2005).

Figure 2 Flow graph of the forward measurement model of the RF section without cross-talk.

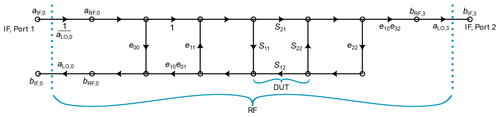
Using this simple representation of a mixer, a signal flow graph representing the frequency translating measurement can be drawn. The flow graph in Figure 2 represents the RF section of the forward measurement model. A similar graph can be constructed for the reverse measurement model, as shown by Rytting (2004). The coefficients of the reverse measurement model are named with a prime symbol in this work. Utilizing the presented flow graph, the raw measured S-parameters of the IF and RF signals can be represented as:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& S_{\text{11}}^{\text{M}}={\displaystyle \frac{b_{\text{IF,0}}}{a_{\text{IF,0}}}}={\displaystyle \frac{b_{\text{RF,0}}\cdot a_{\text{LO,0}}}{a_{\text{RF,0}}\cdot a_{\text{LO,0}}}}\text{and}\\ & S_{\text{21}}^{\text{M}}={\displaystyle \frac{b_{\text{IF,3}}}{a_{\text{IF,0}}}}={\displaystyle \frac{b_{\text{RF,3}}\cdot a_{\text{LO,3}}}{a_{\text{RF,0}}\cdot a_{\text{LO,0}}}}.\end{array}\end{array}$$

The error correction takes into account all constant imperfections of the measurement set-up and VNA itself. However, cable movement during or after calibration is not accounted for by the error correction. Therefore, a term δa_LO,3 is considered here. It represents the influence of the LO cable movement after calibration. The change in the raw measured S-parameter values can be expressed as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }{S}_{\text{11}}^{\text{M}}{\displaystyle }={\displaystyle \frac{b_{\text{IF,0}}}{a_{\text{IF,0}}}}={\displaystyle \frac{b_{\text{RF,0}}\cdot \mathit{\delta }{a}_{\text{LO,0}}}{a_{\text{RF,0}}\cdot \mathit{\delta }{a}_{\text{LO,0}}}},\end{array}$$

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& S_{\text{21}}^{\text{M}}={\displaystyle \frac{b_{\text{IF,3}}}{a_{\text{IF,0}}}}={\displaystyle \frac{b_{\text{RF,3}}\cdot \mathit{\delta }{a}_{\text{LO,3}}}{a_{\text{RF,0}}\cdot \mathit{\delta }{a}_{\text{LO,0}}}}={\displaystyle \frac{b_{\text{RF,3}}}{a_{\text{RF,0}}}}\cdot \mathit{\delta }\text{and}\\ & S_{\text{12}}^{\text{M}}={\displaystyle \frac{b_{\text{IF,0}}}{a_{\text{IF,3}}}}={\displaystyle \frac{b_{\text{RF,0}}\cdot \mathit{\delta }{a}_{\text{LO,0}}}{a_{\text{RF,3}}\cdot \mathit{\delta }{a}_{\text{LO,3}}}}={\displaystyle \frac{b_{\text{RF,0}}}{a_{\text{RF,3}}}}\cdot {\displaystyle \frac{\mathrm{1}}{\mathit{\delta }}}.\end{array}\end{array}$$

Equation (3) shows that a cable movement after calibration has no impact on the reflection coefficient measurement, as the same signal is used for up and down conversion. However, from Eq. (4), it can be seen that there is a non-reciprocal impact of the error δ on transmission measurement raw values because LO signals with different phases are now used. The impact of this phase error in the LO signal is identical for forward and backward transmission; only the sign differs.

However, in practice, reflection measurements are commonly employed to test the impact of cable movements, as presented in the CG-12 (Zeier et al., 2018). The results from such tests are not directly applicable to transmission measurements.

2.1 Compensation of the LO phase error

The error corrected transmission terms using the 12-term model with frequency conversion are

$$\begin{array}{}\text{(5)}& \begin{array}{rl}& S_{\text{21}}={\displaystyle \frac{\left(\frac{S_{\text{21}}^{\text{M}}-e_{\text{30}}}{e_{\text{10}}{e}_{\text{32}}}\right)\cdot \left[\mathrm{1}+\left(\frac{S_{\text{22}}^{\text{M}}{e}_{\text{33}}^{\prime }}{e_{\text{23}}^{\prime }{e}_{\text{32}}^{\prime }}\right)\left(e_{\text{22}}^{\prime }-e_{\text{22}}\right)\right]}{D}}\text{and}\\ & S_{\text{12}}={\displaystyle \frac{\left(\frac{S_{\text{12}}^{\text{M}}-e_{\text{03}}^{\prime }}{e_{\text{10}}^{\prime }{e}_{\text{32}}^{\prime }}\right)\cdot \left[\mathrm{1}+\left(\frac{S_{\text{11}}^{\text{M}}{e}_{\text{00}}}{e_{\text{10}}{e}_{\text{01}}}\right)\left(e_{\text{11}}-e_{\text{11}}^{\prime }\right)\right]}{D}}\text{, with}\end{array}\end{array}$$

$$\begin{array}{}\text{(6)}& \begin{array}{rl}& D=\left[\mathrm{1}+\left({\displaystyle \frac{S_{\text{11}}^{\text{M}}{e}_{\text{00}}}{e_{\text{10}}{e}_{\text{01}}}}\right)e_{\text{11}}\right]\left[\mathrm{1}+\left({\displaystyle \frac{S_{\text{22}}^{\text{M}}{e}_{\text{33}}^{\prime }}{e_{\text{23}}^{\prime }{e}_{\text{32}}^{\prime }}}\right)e_{\text{22}}^{\prime }\right]\\ & -\left({\displaystyle \frac{S_{\text{21}}^{\text{M}}-e_{\text{30}}}{e_{\text{10}}{e}_{\text{32}}}}\right)\left({\displaystyle \frac{S_{\text{12}}^{\text{M}}-e_{\text{03}}^{\prime }}{e_{\text{23}}^{\prime }{e}_{\text{01}}^{\prime }}}\right)e_{\text{22}}{e}_{\text{11}}^{\prime }.\end{array}\end{array}$$

Here, the coefficients with a prime symbol belong to the reverse measurement and e₃₀ denotes cross-talk, which is commonly negligible and not shown in Fig. 2. For measurements with negligible cross-talk, meaning $e_{\text{30}}\approx e_{\text{03}}^{\prime }\approx \mathrm{0}$, the reflection parameters S₁₁ and S₂₂, as well as the factor D, are immune to the error caused by LO cable movement after calibration because the error is compensated by a product of $S_{\mathrm{21}}^M$ and $S_{\mathrm{12}}^M$.

$$\begin{array}{}\text{(7)}& \begin{array}{rl}D& \approx \left[\mathrm{1}+\left({\displaystyle \frac{S_{\text{11}}^{\text{M}}{e}_{\text{00}}}{e_{\text{10}}{e}_{\text{01}}}}\right)e_{\text{11}}\right]\left[\mathrm{1}+\left({\displaystyle \frac{S_{\text{22}}^{\text{M}}{e}_{\text{33}}^{\prime }}{e_{\text{23}}^{\prime }{e}_{\text{32}}^{\prime }}}\right)e_{\text{22}}^{\prime }\right]\\ & -\left({\displaystyle \frac{S_{\text{21}}^{\text{M}}}{e_{\text{10}}{e}_{\text{32}}}}\right)\left({\displaystyle \frac{S_{\text{12}}^{\text{M}}}{e_{\text{23}}^{\prime }{e}_{\text{01}}^{\prime }}}\right)e_{\text{22}}{e}_{\text{11}}^{\prime }\end{array}\end{array}$$

Without cross-talk the transmission parameters in Eq. (5) can be rewritten using Eq. (4) to

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{S}_{\text{21}}& \approx {\displaystyle \frac{\left(\frac{S_{\text{21}}^{\text{M}}}{e_{\text{10}}{e}_{\text{32}}}\right)\cdot \left[\mathrm{1}+\left(\frac{S_{\text{22}}^{\text{M}}{e}_{\text{33}}^{\prime }}{e_{\text{23}}^{\prime }{e}_{\text{32}}^{\prime }}\right)\left(e_{\text{22}}^{\prime }-e_{\text{22}}\right)\right]}{D}}\\ & =\mathit{\delta }\cdot {\displaystyle \frac{\left(\frac{\frac{b_{\text{RF,3}}}{a_{\text{RF,0}}}}{e_{\text{10}}{e}_{\text{32}}}\right)\cdot \left[\mathrm{1}+\left(\frac{S_{\text{22}}^{\text{M}}{e}_{\text{33}}^{\prime }}{e_{\text{23}}^{\prime }{e}_{\text{32}}^{\prime }}\right)\left(e_{\text{22}}^{\prime }-e_{\text{22}}\right)\right]}{D}}\\ & =S_{\text{21}}^{\text{True}}\mathit{\delta }\text{and}\end{array}\end{array}$$

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{S}_{\text{12}}& \approx {\displaystyle \frac{\left(\frac{S_{\text{12}}^{\text{M}}}{e_{\text{10}}^{\prime }{e}_{\text{32}}^{\prime }}\right)\cdot \left[\mathrm{1}+\left(\frac{S_{\text{11}}^{\text{M}}{e}_{\text{00}}}{e_{\text{10}}{e}_{\text{01}}}\right)\left(e_{\text{11}}-e_{\text{11}}^{\prime }\right)\right]}{D}}\\ & ={\displaystyle \frac{\mathrm{1}}{\mathit{\delta }}}\cdot {\displaystyle \frac{\left(\frac{b_{\text{RF,0}}}{a_{\text{RF,3}}}{e}_{\text{10}}^{\prime }{e}_{\text{32}}^{\prime }\right)\cdot \left[\mathrm{1}+\left(\frac{S_{\text{11}}^{\text{M}}{e}_{\text{00}}}{e_{\text{10}}{e}_{\text{01}}}\right)\left(e_{\text{11}}-e_{\text{11}}^{\prime }\right)\right]}{D}}\\ & =S_{\text{21}}^{\text{True}}{\displaystyle \frac{\mathrm{1}}{\mathit{\delta }}}.\end{array}\end{array}$$

Therefore, the transmission factor of the DUT in both the forward and backward direction can be described as the product of a true value $S_{\text{21}}^{\text{True}}$ and $S_{\text{12}}^{\text{True}}$ with a complex phase-shifting term δ. In the case of negligible cross-talk, this term δ is identical for raw and calibrated measurement results. The true values are

$$\begin{array}{}\text{(10)}& S_{\text{12}}^{\text{True}}=\mathit{\delta }{S}_{\text{12}}\text{and}{S}_{\text{21}}^{\text{True}}={\displaystyle \frac{\mathrm{1}}{\mathit{\delta }}}{S}_{\text{21}}.\end{array}$$

3 Measurements

In the experiment shown in Fig. 3, R 900 (WR 10) VNA frequency extenders in the range of 75 to 110 GHz are used. To examine the impact of changes in the LO signal, a phase shifter is introduced into the LO signal path of one extender. A thru reflect line (TRL) calibration is performed and a direct thru connection of the waveguide interfaces in the reference plane is measured repeatedly with different phase shifter settings. This set-up enables systematic investigation of the effects of a change in the LO signal as it might be caused by drift or cable movements after calibration.

Figure 3 Overview of the measurement set-up using WR-10 waveguide extenders and a phase shifter in the LO signal path.

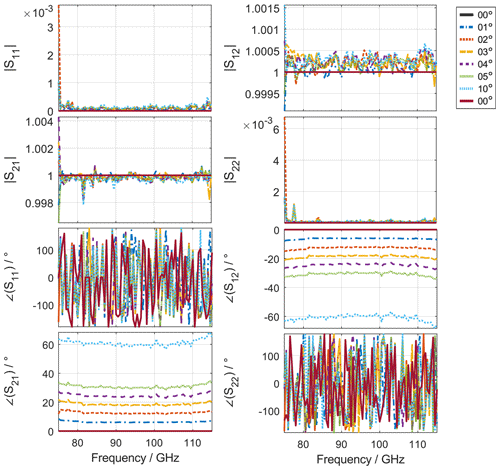
Figure 4 S-Parameter measurement results for a thru with phase shifter settings from 0 to 10° in the LO signal path.

The measurement result depicted in Fig. 4 confirms the expectations from the theory discussed in Sect. 2, that the LO signal phase has only a minor impact on the magnitude of the thru S-parameters, while there is a significant impact on the measured phase of the transmission parameter of the thru. Due to noise, it is not possible to make reliable statements regarding the phase of the well-matched reflection parameters of the thru connection. This results from the multiplication of the LO signal in the VNA extender box.

The multiplication factor N for the LO signal in the R 900 VNA extenders used here is N=6. Therefore, adjusting the phase shifter in the LO signal path to α causes a phase shift at VNA port two of approximately N⋅α in the a_RF,3 and b_RF,3 waves. Figure 4 confirms this; for example, a setting of 1° results in a phase shift of 6° in the measured result. Additionally, it is evident that the phase of the two transmission coefficients is affected with opposite signs. We conducted measurements with the phase shifter setting of 0° as both the first and last measurement. However, the results demonstrate high repeatability, and no discernible difference can be observed from the plot in Fig. 4.

4 Consideration and Correction

The phase error δ caused by LO cable movements after calibration can be determined by measuring one reciprocal DUT in each cable position and using $S_{\text{21}}^{\text{True}}=S_{\text{12}}^{\text{True}}$. All measurements in one cable position can then be corrected using

$$\begin{array}{}\text{(11)}& \mathit{\delta }{S}_{\text{12}}={\displaystyle \frac{\mathrm{1}}{\mathit{\delta }}}{S}_{\text{21}}\iff \mathit{\delta }=\pm \sqrt{{\displaystyle \frac{S_{\text{21}}}{S_{\text{12}}}}}=\left\{\begin{array}{l}+\sqrt{\frac{S_{\text{21}}}{S_{\text{12}}}}\\ -\sqrt{\frac{S_{\text{21}}}{S_{\text{12}}}}={\text{e}}^{j\mathit{\pi }}\cdot \sqrt{\frac{S_{\text{21}}}{S_{\text{12}}}}.\end{array}\right.\end{array}$$

Since the phase error δ can only be determined unambiguously within ±180°, the LO signal cable movement should still be kept to a minimum. However, for most cables and scenarios this should be no problem.

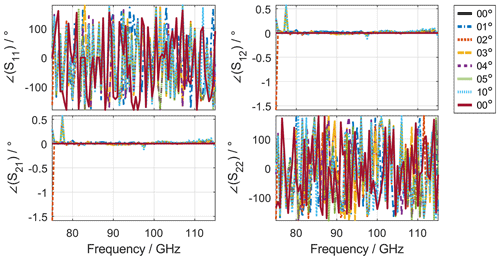
Figure 5 Phase angle measurement result shown in Fig. 4 with applied correction making the phase angle of the Thru measurements reciprocal.

In Fig. 5, the phase angle of the measurement result is shown again, this time with the correction applied. It can be observed that the measurement result for the phase angle of thru connections is now almost independent of the setting of the phase shifter in the LO signal path, confirming the proposed correction in Eq. (11). In most measurement scenarios, it is sufficient to move only one frequency extender. However, if cable movements on several ports are necessary or there is significant drift for another reason, this correction can be applied simultaneously to several ports. This is because the errors from the LO signal change on each port are linearly superimposed in the measurement result.

Alternatively, the LO cable movement could be characterized and regarded as a source of measurement uncertainty for the transmission coefficient phase. However, due to the multiplication factor α of the VNA frequency extenders, this MU contribution would be rather significant. In Schramm et al. (2024), measurement uncertainties and uncertainty budgets for waveguide measurements are presented. The additional term due to local oscillator cable movement would presumably dominate the uncertainty budgets for the phase angle of the transmission terms. Therefore, a correction is preferable.

5 Conclusions

In this study, we explored the impact of LO signal variations in VNA measurements, akin to the disturbances induced by cable movements post-calibration. Through theoretical analysis and experimental demonstrations utilizing a phase shifter to intentionally induce signal variations, we systematically examined the effect of LO signal changes. Our experiment demonstrated that even minor phase changes in the LO signal after calibration can significantly affect the measured phase angle of the transmission coefficients, attributed to the multiplication factor N of the VNA frequency extenders. By deriving error correction terms, including the frequency translating components, we formulated a correction method for the non-reciprocal error and applied it to our experimental data. Our results demonstrate that the corrected measurements remain unaffected by fluctuations in the LO signal, underscoring the robustness of our correction approach. This study contributes to enhancing the accuracy and reliability of VNA measurements, particularly in scenarios where LO signal variations could potentially introduce errors.