A full wave description for thin wire structures with TLST and perturbation theory

A full wave description of a thin wire structure, that includes mutual interactions and radiation, can be obtained in closed form with the so-called Transmission Line Super Theory or a refined variant of this method that utilises perturbation theory. In either procedure, a set of mixed potential integral equations is solved for the currents that propagate along a wire. With the perturbation approach, no iteration is required to approximate the initial current distribution on the wire. This procedure will be applied to solve multi-wire problems. The theory will be derived and computed results will be shown to be in good agreement with method of moment computations.

1 Introduction

The solution to electromagnetic compatibility problems becomes more challenging if a large number of electronic devices or modules of a system is placed in a confined space. Mutual interactions and especially mutual coupling between wires connecting individual modules might occur, which can lead to malfunctions and undesired system conditions. In order to circumvent erratic system performance, an accurate estimation of the coupling parameters is necessary.

The Transmission Line Super Theory (TLST) is an iterative procedure (Nitsch et al., 2009), where the wire parameters like the inductance and capacitance per unit length are first determined under the assumption to be dependent upon position only. Frequency dependence is accounted for in the subsequent iterations. With these parameters, a system of ordinary differential equations of first order with variable coefficients is established and solved for the unknown currents with the aid of a matrizant, but the solution of the resulting system of equations is computationally extensive. A perturbation approach for the TLST was formulated in Nitsch and Tkachenko (2010).

In the perturbation method, the currents to be determined are initially approximated with values calculated using the conventional transmission line theory. These currents are subsequently employed to compute the parameters of the wire structure using mixed potential integral equations (MPIE). The parameters are then used in a system of ordinary differential equations similar to the TLST to ascertain the currents on the wires. In contrast to the TLST, it is not necessary in the perturbation method to determine the wire parameters in a first iteration, which therefore requires less computation time. The theoretical formulation of the perturbation approach in Nitsch and Tkachenko (2010) provides the basis for this investigation. The procedure will be derived and applied to the solution of multi-wire problems. Section 2 facilitates essential background theory. The TLST is described in Sect. 3 where a detailed derivation of the perturbation theory is given in Sect. 3.2. Simulated results are shown in Sect. 4 which are validated by comparison with method of moment computations.

2 Background theory

The TLST is based on the solution of the Helmholtz equations

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{\Delta }\underset{\mathrm{¯}}{\mathit{A}}+k^{\mathrm{2}}\underset{\mathrm{¯}}{\mathit{A}}=-\mathit{\mu }{\underset{\mathrm{¯}}{\mathit{J}}}^s\end{array}$$

and

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathrm{\Delta }\underset{\mathrm{¯}}{\mathit{\varphi }}+k^{\mathrm{2}}\underset{\mathrm{¯}}{\mathit{\varphi }}=-{\displaystyle \frac{\underset{\mathrm{¯}}{\mathit{\varrho }}}{\mathit{\epsilon }}}.\end{array}$$

for the magnetic vector potential $\underset{\mathrm{¯}}{\mathit{A}}$ and the electric scalar potential $\underset{\mathrm{¯}}{\mathit{\varphi }}$. ${\underset{\mathrm{¯}}{\mathit{J}}}^s$ denotes an impressed current density and $\underset{\mathrm{¯}}{\mathit{\varrho }}$ a charge density. The wave number k is given by

$$\begin{array}{}\text{(3)}& {\displaystyle }k=\mathit{\omega }\sqrt{\mathit{\mu }\mathit{\epsilon }}.\end{array}$$

where μ is the permeability and ε the permittivity of the medium. For sources above a perfectly conducting ground plane, the two potentials are determined by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{\mathrm{¯}}{\mathit{A}}\left(\mathit{r}\right)={\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}\int \int \underset{D}{\int }{\underset{\mathrm{¯}}{\mathit{J}}}^s\left({\mathit{r}}^{\prime }\right){\displaystyle \frac{e^{-jk|\mathit{r}-{\mathit{r}}^{\prime }|}}{|\mathit{r}-{\mathit{r}}^{\prime }|}}\\ \text{(4)}& {\displaystyle }& {\displaystyle }+{\underset{\mathrm{¯}}{\mathit{J}}}_{\mathrm{1}}^s\left({{\mathit{r}}^{\prime }}_{\mathrm{1}}\right){\displaystyle \frac{e^{-jk|\mathit{r}-{{\mathit{r}}^{\prime }}_{\mathrm{1}}|}}{|\mathit{r}-{{\mathit{r}}^{\prime }}_{\mathrm{1}}|}}\text{d}{\mathit{\tau }}_D\end{array}$$

and

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{\mathrm{¯}}{\mathit{\varphi }}\left(\mathit{r}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }\mathit{\epsilon }}}\int \int \underset{D}{\int }\underset{\mathrm{¯}}{\mathit{\varrho }}\left({\mathit{r}}^{\prime }\right){\displaystyle \frac{e^{-jk|\mathit{r}-{\mathit{r}}^{\prime }|}}{|\mathit{r}-{\mathit{r}}^{\prime }|}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }-\underset{\mathrm{¯}}{\mathit{\varrho }}\left({{\mathit{r}}^{\prime }}_{\mathrm{1}}\right){\displaystyle \frac{e^{-jk|\mathit{r}-{{\mathit{r}}^{\prime }}_{\mathrm{1}}|}}{|\mathit{r}-{{\mathit{r}}^{\prime }}_{\mathrm{1}}|}}\text{d}{\mathit{\tau }}_D.\end{array}$$

r represents the vector to the field point, r^′ the vector to the source point, ${{\mathit{r}}^{\prime }}_{\mathrm{1}}$ the vector to the image of the source point, and ${\underset{\mathrm{¯}}{\mathit{J}}}_{\mathrm{1}}^s\left({{\mathit{r}}^{\prime }}_{\mathrm{1}}\right)$ the image current density. D is the source volume and dτ_D a volume element.

The electric field is given by the sum of the scattered field and the exciting or incident field,

$$\begin{array}{}\text{(6)}& {\displaystyle }\underset{\mathrm{¯}}{\mathit{E}}\left(\mathit{r}\right)={\underset{\mathrm{¯}}{\mathit{E}}}^{\text{scat}}\left(\mathit{r}\right)+{\underset{\mathrm{¯}}{\mathit{E}}}^{\text{inc}}\left(\mathit{r}\right).\end{array}$$

The scattered field is given by

$$\begin{array}{}\text{(7)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathit{E}}}^{\text{scat}}\left(\mathit{r}\right)=-j\mathit{\omega }\underset{\mathrm{¯}}{\mathit{A}}\left(\mathit{r}\right)-\mathrm{grad}\underset{\mathrm{¯}}{\mathit{\varphi }}\left(\mathit{r}\right).\end{array}$$

The electric field and the potentials on the surface S of the source volume are related through the boundary conditions

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\left.\underset{\mathrm{¯}}{\mathit{E}}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S={\displaystyle \frac{\mathrm{1}}{\mathit{\varkappa }}}{\left.{\underset{\mathrm{¯}}{\mathit{J}}}^s\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S\\ \text{(8)}& {\displaystyle }& {\displaystyle }={\left.{\underset{\mathrm{¯}}{\mathit{E}}}^{\text{scat}}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S+{\left.{\underset{\mathrm{¯}}{\mathit{E}}}^{\text{inc}}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S\end{array}$$

and

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\mathrm{1}}{\mathit{\varkappa }}}{\left.{\underset{\mathrm{¯}}{\mathit{J}}}^s\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S=-j\mathit{\omega }{\left.\underset{\mathrm{¯}}{\mathit{A}}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S\\ \text{(9)}& {\displaystyle }& {\displaystyle }-{\left.\mathrm{grad}\underset{\mathrm{¯}}{\mathit{\varphi }}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S+{\left.{\underset{\mathrm{¯}}{\mathit{E}}}^{\text{inc}}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S.\end{array}$$

Applying the thin wire approximation (Nitsch et al., 2009), where the current is concentrated on the axis of the wire which possesses a small radius a (Nitsch and Tkachenko, 2010), and substituting of Eqs. (4) and (5) into Eq. (9) leads to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }j\mathit{\omega }{\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}\underset{\mathrm{0}}{\overset{L}{\int }}{\underset{\mathrm{¯}}{G}}_A(l,l^{\prime }){\underset{\mathrm{¯}}{I}}^s\left(l^{\prime }\right)\text{d}{l}^{\prime }+{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }\mathit{\epsilon }}}{\displaystyle \frac{\partial }{\partial l}}\underset{\mathrm{0}}{\overset{L}{\int }}\underset{\mathrm{¯}}{\mathit{\lambda }}\left(l^{\prime }\right){\underset{\mathrm{¯}}{G}}_{\mathit{\varphi }}(l,l^{\prime })\text{d}{l}^{\prime }\\ \text{(10)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{C_{\text{c}}^{\prime }}}{\displaystyle \frac{\partial }{\partial l}}\underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)+{\underset{\mathrm{¯}}{Z}}^{\prime }{\underset{\mathrm{¯}}{I}}^s\left(l\right)={\underset{\mathrm{¯}}{\mathit{E}}}^{\text{inc}}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right),\end{array}$$

where ${\underset{\mathrm{¯}}{I}}^s$ represents the current in the wire and $\underset{\mathrm{¯}}{\mathit{\lambda }}$ the line charge density. ${\underset{\mathrm{¯}}{G}}_A$ and ${\underset{\mathrm{¯}}{G}}_{\mathit{\varphi }}$ denote the Green's functions for the potentials, given by

$$\begin{array}{ll}{\displaystyle }{\underset{\mathrm{¯}}{G}}_A(l,l^{\prime })& {\displaystyle }={\displaystyle \frac{e^{-jk\left|\mathit{r}\right(l)-{\mathit{r}}^{\prime }(l^{\prime }\left)\right|}}{\left|\mathit{r}\right(l)-{\mathit{r}}^{\prime }(l^{\prime }\left)\right|}}{\mathit{e}}_t\left(l\right)\cdot {\mathit{e}}_t\left(l^{\prime }\right)\\ \text{(11)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{e^{-jk\left|\mathit{r}\right(l)-{{\mathit{r}}^{\prime }}_{\mathrm{1}}(l^{\prime }\left)\right|}}{\left|\mathit{r}\right(l)-{{\mathit{r}}^{\prime }}_{\mathrm{1}}(l^{\prime }\left)\right|}}{\mathit{e}}_t\left(l\right)\cdot {\mathit{e}}_t{}_{{}_{\mathrm{1}}}\left(l^{\prime }\right),\text{(12)}& {\displaystyle }{\underset{\mathrm{¯}}{G}}_{\mathit{\varphi }}(l,l^{\prime })& {\displaystyle }={\displaystyle \frac{e^{-jk\left|\mathit{r}\right(l)-{\mathit{r}}^{\prime }(l^{\prime }\left)\right|}}{\left|\mathit{r}\right(l)-{\mathit{r}}^{\prime }(l^{\prime }\left)\right|}}-{\displaystyle \frac{e^{-jk\left|\mathit{r}\right(l)-{{\mathit{r}}^{\prime }}_{\mathrm{1}}(l^{\prime }\left)\right|}}{\left|\mathit{r}\right(l)-{{\mathit{r}}^{\prime }}_{\mathrm{1}}(l^{\prime }\left)\right|}}.\end{array}$$

In case of a lossy conductor in the thin wire approximation, the tangential $\underset{\mathrm{¯}}{\mathit{E}}$-field becomes

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\mathrm{1}}{\mathit{\varkappa }}}{\left.{\underset{\mathrm{¯}}{\mathit{J}}}^s\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right)\right|}_S={\underset{\mathrm{¯}}{Z}}^{\prime }{\underset{\mathrm{¯}}{I}}^s\left(l\right),\end{array}$$

with the impedance per unit length

$$\begin{array}{}\text{(14)}& {\displaystyle }{\underset{\mathrm{¯}}{Z}}^{\prime }=-{\displaystyle \frac{{\underset{\mathrm{¯}}{Z}}_{\text{c}}}{\mathrm{2}\mathit{\pi }a}}{\displaystyle \frac{I_{\mathrm{0}}\left(\underset{\mathrm{¯}}{\mathit{\gamma }}a\right)}{I_{\mathrm{1}}\left(\underset{\mathrm{¯}}{\mathit{\gamma }}a\right)}}\end{array}$$

evaluated on the surface of the wire (Nitsch and Tkachenko, 2006; Tesche et al., 1997). The characteristic impedance ${\underset{\mathrm{¯}}{Z}}_{\text{c}}$ is

$$\begin{array}{}\text{(15)}& {\displaystyle }{\underset{\mathrm{¯}}{Z}}_{\text{c}}=\sqrt{{\displaystyle \frac{j\mathit{\omega }\mathit{\mu }}{\mathit{\varkappa }+j\mathit{\omega }\mathit{\epsilon }}}}.\end{array}$$

For a dielectrically coated wire an additional capacitance $C_{\text{c}}^{\prime }$ needs to be considered in Eq. (10), which is given by

$$\begin{array}{}\text{(16)}& {\displaystyle }{C}_{\text{c}}^{\prime }={\displaystyle \frac{\mathrm{2}\mathit{\pi }\mathit{\epsilon }}{\ln \frac{b}{a}}}{\displaystyle \frac{{\mathit{\epsilon }}_{\text{c}}}{{\mathit{\epsilon }}_{\text{c}}-\mathrm{1}}}.\end{array}$$

An alternative formulation to Eq. (10) can be established by substituting Eq. (4) in Eq. (9), which yields

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\partial \underset{\mathrm{¯}}{\mathit{\varphi }}}{\partial l}}+j\mathit{\omega }{\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}\underset{\mathrm{0}}{\overset{L}{\int }}{\underset{\mathrm{¯}}{G}}_A(l,l^{\prime }){\underset{\mathrm{¯}}{I}}^s\left(l^{\prime }\right)\text{d}{l}^{\prime }+{\underset{\mathrm{¯}}{Z}}^{\prime }{\underset{\mathrm{¯}}{I}}^s\left(l\right)\\ \text{(17)}& {\displaystyle }& {\displaystyle }={\underset{\mathrm{¯}}{\mathit{E}}}^{\text{inc}}\left(\mathit{r}\right)\cdot {\mathit{e}}_t\left(\mathit{r}\right).\end{array}$$

Employing the continuity condition $\underset{\mathrm{¯}}{\mathit{\lambda }}=-\frac{\mathrm{1}}{j\mathit{\omega }}{\underset{\mathrm{¯}}{I}}^s$ in conjunction with the thin wire approximation in Eq. (5) leads to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{\mathrm{¯}}{\mathit{\varphi }}\left(l\right)+{\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }\mathrm{4}\mathit{\pi }\mathit{\epsilon }}}\underset{\mathrm{0}}{\overset{L}{\int }}{\underset{\mathrm{¯}}{G}}_{\mathit{\varphi }}(l,l^{\prime }){\displaystyle \frac{\partial {\underset{\mathrm{¯}}{I}}^s\left(l^{\prime }\right)}{\partial l^{\prime }}}\text{d}{l}^{\prime }\\ \text{(18)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }{C}_{\text{c}}^{\prime }}}{\displaystyle \frac{\partial {\underset{\mathrm{¯}}{I}}^s\left(l\right)}{\partial l}}=\mathrm{0}.\end{array}$$

The current on the wire can now be determined by either solving Eq. (10) or by computing the solution to Eqs. (17) and (18). This will be outlined for multi-wire problems in Sect. 3.1 using transmission line theory based on Eq. (10), and by applying perturbation theory to Eqs. (17) and (18) in Sect. 3.2.

Figure 1 Point on wire j and segment i as function of the global parameter l, shown for l=0.8.

3 Full-wave transmission line theory

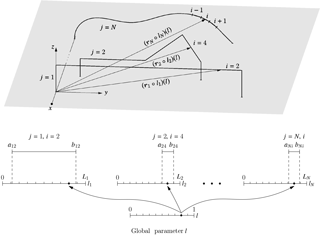
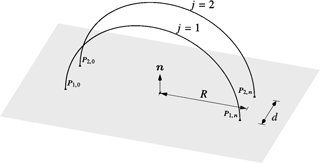
In order to solve multi-wire problems, a single parameter is required to simultaneously reference points on all the wires. This can be achieved with the mapping

$$\begin{array}{}\text{(19)}& {\displaystyle }{l}_j=l{L}_j\text{with}\mathrm{0}\le l\le \mathrm{1},\end{array}$$

on wire j of length L_j with $j=\mathrm{1},\mathrm{\dots },N$, where N denotes the number of wires. l_j is a curve length parameter for wire j that depends on the single global parameter l. Figure 1 depicts an example with N wires. Each wire is divided into a number of segments. Arbitrarily curved wires are linearized, so that each segment is straight. The number of segments on a particular wire is as a result dependent on the curvature of the wire. In terms of the curve length parameter l_j, a segment i of wire j extends from a_ji to b_ji, as shown in the figure for three different segments. The linearization leads to a constant tangent vector on a segment. This simplifies the integration considerably, so that Eq. (10) can be written as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }j\mathit{\omega }{\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}\sum _{p=\mathrm{1}}^N\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}{L}_j{\underset{\mathrm{¯}}{G}}_{A,jp}(l{L}_j,l^{\prime }{L}_p){\underset{\mathrm{¯}}{I}}_p^s\left(l^{\prime }{L}_p\right)L_p\text{d}{l}^{\prime }\\ {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }\mathit{\epsilon }}}{\displaystyle \frac{\partial }{\partial l}}\sum _{p=\mathrm{1}}^N\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}{L}_p{\underset{\mathrm{¯}}{G}}_{\mathit{\varphi },jp}(l{L}_j,l^{\prime }{L}_p){\underset{\mathrm{¯}}{\mathit{\lambda }}}_p\text{d}{l}^{\prime }\\ {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{1}}{C_{\text{c}}^{\prime }}}{\displaystyle \frac{\partial }{\partial l}}{\underset{\mathrm{¯}}{\mathit{\lambda }}}_j\left(l{L}_j\right)+{\underset{\mathrm{¯}}{Z}}_j^{\prime }{L}_j{\underset{\mathrm{¯}}{I}}_j^s\left(l{L}_j\right)\\ \text{(20)}& {\displaystyle }& {\displaystyle }=L_j{\underset{\mathrm{¯}}{\mathit{E}}}_j^{\text{inc}}\cdot {\mathit{e}}_{t,j}\left({\mathit{r}}_j\right).\end{array}$$

Equivalently, for Eqs. (17) and (18) it follows

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\partial {\underset{\mathrm{¯}}{\mathit{\varphi }}}_j\left(l\right)}{\partial l}}+j\mathit{\omega }{\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}{L}_j\sum _{p=\mathrm{1}}^N\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}{\underset{\mathrm{¯}}{G}}_{A,jp}(l{L}_j,l^{\prime }{L}_p){\underset{\mathrm{¯}}{I}}_p\left(l^{\prime }{L}_p\right)L_p\text{d}{l}^{\prime }\\ \text{(21)}& {\displaystyle }& {\displaystyle }+{\underset{\mathrm{¯}}{Z}}_j^{\prime }{L}_j{\underset{\mathrm{¯}}{I}}_j^s\left(l{L}_j\right)=L_j{\underset{\mathrm{¯}}{\mathit{E}}}_j^{\text{inc}}\cdot {\mathit{e}}_t\left({\mathit{r}}_j\right)\end{array}$$

and

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathit{\varphi }}}_j\left(l\right)+{\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }\mathrm{4}\mathit{\pi }\mathit{\epsilon }}}\sum _{p=\mathrm{1}}^N\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}{\underset{\mathrm{¯}}{G}}_{\mathit{\varphi },jp}(l{L}_j,l^{\prime }{L}_p){\displaystyle \frac{\partial {\underset{\mathrm{¯}}{I}}_p^s\left(l^{\prime }\right)}{\partial l^{\prime }}}\text{d}{l}^{\prime }\\ \text{(22)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }{C}_{\text{c}}^{\prime }{L}_j}}{\displaystyle \frac{\partial {\underset{\mathrm{¯}}{I}}_j^s\left(l{L}_j\right)}{\partial l}}=\mathrm{0}.\end{array}$$

Alternative parameterizations to Eq. (19) are possible (Nitsch and Tkachenko, 2010), they lead to the same solutions but with slightly different expressions for the entries of the parameter matrices.

3.1 Transmission Line Super Theory

In this section Eq. (20) is solved iteratively using Transmission Line Super Theory (Haase, 2005) with a frequency independent current. Since a transmission line is characterized by the parameters $\stackrel{\mathrm{‾}}{\mathcal{P}}$, the unknown quantities have to be determined before computing the currents. By casting the MPIE into matrix form, a position dependent differential equation system of the form

$$\begin{array}{}\text{(23)}& {\displaystyle \frac{\text{d}}{\text{d}l}}\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{\varphi }}\left(l\right)\\ \underset{\mathrm{¯}}{I}\left(l\right)\end{array}\right)+j\mathit{\omega }\underset{\mathrm{¯}}{\mathcal{P}}\left(l\right)\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{\varphi }}\left(l_{\mathrm{0}}\right)\\ \underset{\mathrm{¯}}{I}\left(l_{\mathrm{0}}\right)\end{array}\right)=\left(\begin{array}{c}{\underset{\mathrm{¯}}{\mathit{\varphi }}}^{\text{inc}}\left(l\right)\\ {\underset{\mathrm{¯}}{I}}^{\text{inc}}\left(l\right)\end{array}\right)\end{array}$$

can be established. The parameters $\underset{\mathrm{¯}}{\mathcal{P}}$ will be determined iteratively, where Eq. (23) is solved using a product integral (Gantmacher, 1960; Dollard and Friedman, 1984). Rewriting Eq. (20) in this form leads to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}j\mathit{\omega }\mathbf{1}& \mathbf{1}\frac{\partial }{\partial l}\end{array}\right)\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{K}}}_L(l,l^{\prime },k)& \mathbf{0}\\ \mathbf{0}& {\underset{\mathrm{¯}}{\mathcal{K}}}_C(l,l^{\prime },k)\end{array}\right)\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{I}}\left(l^{\prime }\right)\\ \underset{\mathrm{¯}}{\mathit{\lambda }}\left(l^{\prime }\right)\end{array}\right)\text{d}{l}^{\prime }\\ \text{(24)}& {\displaystyle }& {\displaystyle }+{\mathcal{C}}_{\text{c}}^{\prime -\mathrm{1}}\underset{\mathrm{¯}}{\mathit{\lambda }}+{\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }\underset{\mathrm{¯}}{\mathit{I}}=\mathbf{0}\end{array}$$

with

$$\begin{array}{}\text{(25)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{K}}}_L(l,l^{\prime },k)& {\displaystyle }={\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}\text{diag}\left(L_j\right){\underset{\mathrm{¯}}{\mathcal{G}}}_A(l,l^{\prime },k),\text{(26)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{K}}}_C(l,l^{\prime },k)& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }\mathit{\epsilon }}}{\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi }}(l,l^{\prime },k).\end{array}$$

The wires are excited at their terminals, which are located outside the source volume and the influence of external fields is neglected. The matrices ${\underset{\mathrm{¯}}{\mathcal{G}}}_A(l,l^{\prime },k)$ and ${\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi }}(l,l^{\prime },k)$ are given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{G}}}_A(l,l^{\prime },k)={\underset{\mathrm{¯}}{G}}_{A,jp}(l{L}_j,l^{\prime }{L}_p)L_p,\\ \text{(27)}& {\displaystyle }& {\displaystyle }j=\mathrm{1},\mathrm{2},\mathrm{\dots },N;p=\mathrm{1},\mathrm{2},\mathrm{\dots },N\end{array}$$

and

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi }}(l,l^{\prime },k)={\underset{\mathrm{¯}}{G}}_{\mathit{\varphi },jp}(l{L}_j,l^{\prime }{L}_p,)\\ \text{(28)}& {\displaystyle }& {\displaystyle }j=\mathrm{1},\mathrm{2},\mathrm{\dots },N;p=\mathrm{1},\mathrm{2},\mathrm{\dots },N.\end{array}$$

Each matrix has the dimension N×N, where N represents the number of wires. The impedance and capacitance matrices have diagonal form and are given by

$$\begin{array}{}\text{(29)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }& {\displaystyle }=\text{diag}\left(L_j\right)\text{diag}\left({\underset{\mathrm{¯}}{Z}}_j^{\prime }\right),\text{ for }j=\mathrm{1},\mathrm{\dots },N,\text{(30)}& {\displaystyle }{\mathcal{C}}_{\text{c}}^{\prime }& {\displaystyle }=\text{diag}\left(L_j\right)\text{diag}\left(C_{\text{c},j}^{\prime }\right),\text{ for }j=\mathrm{1},\mathrm{\dots },N.\end{array}$$

Under the assumption that the line charge and current are determined by the solution of a differential equation system (23), the solution is of the form

$$\begin{array}{}\text{(31)}& {\displaystyle }\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{I}}\left(l^{\prime }\right)\\ \underset{\mathrm{¯}}{\mathit{\lambda }}\left(l^{\prime }\right)\end{array}\right)={\stackrel{\mathrm{̃}}{\underset{\mathrm{¯}}{\mathbf{\Omega }}}}_l^{l^{\prime }}(-j\mathit{\omega }\underset{\mathrm{¯}}{\mathcal{P}})\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)\\ \underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\end{array}\right).\end{array}$$

${\stackrel{\mathrm{̃}}{\underset{\mathrm{¯}}{\mathbf{\Omega }}}}_l^{l^{\prime }}$ denotes the propagator, which is also referred to as matrizant. Employing Eq. (31) in Eq. (24) leads to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}j\mathit{\omega }\mathbf{1}& \mathbf{1}\frac{\partial }{\partial l}\end{array}\right)\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{K}}}_L(l,l^{\prime },k)& \mathbf{0}\\ \mathbf{0}& {\underset{\mathrm{¯}}{\mathcal{K}}}_C(l,l^{\prime },k)\end{array}\right){\stackrel{\mathrm{̃}}{\underset{\mathrm{¯}}{\mathbf{\Omega }}}}_l^{l^{\prime }}\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)\\ \underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\end{array}\right)\text{d}{l}^{\prime }\\ \text{(32)}& {\displaystyle }& {\displaystyle }+{\mathcal{C}}_{\text{c}}^{\prime -\mathrm{1}}\underset{\mathrm{¯}}{\mathit{\lambda }}+{\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }\underset{\mathrm{¯}}{\mathit{I}}=\mathbf{0},\end{array}$$

which can be written as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}j\mathit{\omega }\mathbf{1}& \mathbf{1}\frac{\partial }{\partial l}\end{array}\right)\left(\begin{array}{c}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{11}}(l,k)\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)+{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{12}}(l,k)\underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\\ {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}(l,k)\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)+{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}(l,k)\underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\end{array}\right)\\ \text{(33)}& {\displaystyle }& {\displaystyle }+{\mathcal{C}}_{\text{c}}^{\prime -\mathrm{1}}\underset{\mathrm{¯}}{\mathit{\lambda }}+{\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }\underset{\mathrm{¯}}{\mathit{I}}=\mathbf{0}\end{array}$$

where the submatrices ${\underset{\mathrm{¯}}{\mathcal{R}}}_{ij}$ contain the solutions of the integrals. Applying the product rule of differentiation, a more compact expression in terms of current and charge can be found if the equation of continuity is applied,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}& {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}\\ \mathbf{1}& \mathbf{0}\end{array}\right)\left(\begin{array}{c}\frac{\partial }{\partial l}\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)\\ \frac{\partial }{\partial l}\underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\end{array}\right)\\ {\displaystyle }& {\displaystyle }+j\mathit{\omega }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{11}}+\frac{\mathrm{1}}{j\mathit{\omega }}\left(\frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}+{\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }\right)& {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{12}}+\frac{\mathrm{1}}{j\mathit{\omega }}\left(\frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}+{\mathcal{C}}_{\text{c}}^{\prime -\mathrm{1}}\right)\\ \mathbf{0}& \mathbf{1}\end{array}\right)\\ \text{(34)}& {\displaystyle }& {\displaystyle }\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)\\ \underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\end{array}\right)=\mathbf{0}.\end{array}$$

This can be rearranged as

$$\begin{array}{}\text{(35)}& {\displaystyle \frac{\partial }{\partial l}}\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)\\ \underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\end{array}\right)+j\mathit{\omega }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\text{iq}}\left(l\right)\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{I}}\left(l\right)\\ \underset{\mathrm{¯}}{\mathit{\lambda }}\left(l\right)\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right),\end{array}$$

which is a differential equation system for current and line charge. The parameter matrix ${\underset{\mathrm{¯}}{\mathcal{P}}}_{\text{iq}}(l,k)$ follows from Eqs. (34) and (35),

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\text{iq}}(l,k)={\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}& {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}\\ \mathbf{1}& \mathbf{0}\end{array}\right)}^{-\mathrm{1}}\\ \text{(36)}& {\displaystyle }& {\displaystyle }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{11}}+\frac{\mathrm{1}}{j\mathit{\omega }}\left(\frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}+{\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }\right)& {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{12}}+\frac{\mathrm{1}}{j\mathit{\omega }}\left(\frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}+{\mathcal{C}}_{\text{c}}^{\prime -\mathrm{1}}\right)\\ \mathbf{0}& \mathbf{1}\end{array}\right).\end{array}$$

The submatrices ${\underset{\mathrm{¯}}{\mathcal{R}}}_{ij}$ matrices are unknown and have to be determined in order to obtain the parameters of the transmission line system. Assuming that the matrizant is known, the integral over the Green's functions can be solved and the submatrices can be obtained from Eq. (32), and combined in a matrix $\underset{\mathrm{¯}}{\mathcal{R}}$ of the form

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{\mathrm{¯}}{\mathcal{R}}=\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{11}}& {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{12}}\\ {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}& {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}\end{array}\right)\\ \text{(37)}& {\displaystyle }& {\displaystyle }=\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{K}}}_L(l,l^{\prime },k)& \mathbf{0}\\ \mathbf{0}& {\underset{\mathrm{¯}}{\mathcal{K}}}_C(l,l^{\prime },k)\end{array}\right){\stackrel{\mathrm{̃}}{\underset{\mathrm{¯}}{\mathbf{\Omega }}}}_l^{l^{\prime }}\text{d}{l}^{\prime }.\end{array}$$

At this point the iteration is started. The identity matrix is used as a first approximation for the matrizant. Assuming the Green's functions initially to be independent of frequency, allows integrals to be solved analytically (Nitsch et al., 2009). The initial values are then

$$\begin{array}{}\text{(38)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{R}}}^{\left(\mathrm{0}\right)}=\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}{\left.\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{K}}}_L(l,l^{\prime })& \mathbf{0}\\ \mathbf{0}& {\underset{\mathrm{¯}}{\mathcal{K}}}_C(l,l^{\prime })\end{array}\right)\right|}_{k=\mathrm{0}}\text{d}{l}^{\prime }.\end{array}$$

Based on these values, the parameters ${\underset{\mathrm{¯}}{\mathcal{P}}}_{\text{iq}}^{\left(\mathrm{0}\right)}\left(l\right)$ are calculated using Eq. (36), from which an updated solution for current and line charge is computed employing Eq. (35) and then recasted in a form of a matrizant as written in Eq. (31). The next iteration is performed with the updated matrizant. The iteration matrix at step n can now be compactly expressed as

$$\begin{array}{}\text{(39)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{R}}}^{\left(n\right)}=\left\{\begin{array}{l}\underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}{\left.\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{K}}}_L(l,l^{\prime })& \mathbf{0}\\ \mathbf{0}& {\underset{\mathrm{¯}}{\mathcal{K}}}_C(l,l^{\prime })\end{array}\right)\right|}_{k=\mathrm{0}}\text{d}{l}^{\prime },\\ n=\mathrm{0}\\ \\ \underset{\mathrm{0}}{\overset{\mathrm{1}}{\int }}\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{K}}}_L(l,l^{\prime },k)& \mathbf{0}\\ \mathbf{0}& {\underset{\mathrm{¯}}{\mathcal{K}}}_C(l,l^{\prime },k)\end{array}\right){\stackrel{\mathrm{̃}}{\underset{\mathrm{¯}}{\mathbf{\Omega }}}}_{\mathrm{0}}^{l^{\prime }}(-j\mathit{\omega }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\text{iq}}^{(n-\mathrm{1})})\text{d}{l}^{\prime },\\ \text{otherwise}.\end{array}\right.\end{array}$$

Usually, the first iteration already delivers accurate results (Haase, 2005). In order to solve the differential equations, boundary conditions are required for current and line charge, which is a non-trivial problem for the charge. In order to circumvent this problem, a potential and current representation is employed. From Eq. (33) it follows

$$\begin{array}{}\text{(40)}& {\displaystyle }\underset{\mathrm{¯}}{\mathit{\varphi }}={\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}\underset{\mathrm{¯}}{\mathit{I}}+{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}\underset{\mathrm{¯}}{\mathit{\lambda }},\end{array}$$

from which parameters ${\underset{\mathrm{¯}}{\mathcal{P}}}^{\star }$ can be computed, (Haase, 2005),

$$\begin{array}{}\text{(41)}& {\underset{\mathrm{¯}}{\mathcal{P}}}^{\star }=\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{11}}^{\star }& {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{12}}^{\star }\\ {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{21}}^{\star }& {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{22}}^{\star }\end{array}\right),\end{array}$$

where

$$\begin{array}{ll}{\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{11}}^{\star }& {\displaystyle }=\left({\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{12}}+{\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }}}{{\mathcal{C}}_{\text{c}}^{\prime }}^{-\mathrm{1}}\right){\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}^{-\mathrm{1}}\\ {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{12}}^{\star }& {\displaystyle }={\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{11}}+{\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }}}\left({\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }-{{\mathcal{C}}_{\text{c}}^{\prime }}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}\right)-{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{12}}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}\\ {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{21}}^{\star }& {\displaystyle }={\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}^{-\mathrm{1}}\\ {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{22}}^{\star }& {\displaystyle }=-{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{21}}\end{array}$$

The iterative approach is based on the computation of $\underset{\mathrm{¯}}{\mathcal{R}}$, which is then used in Eq. (41). Solving the differential equation in potential-current representation leads to the desired result (Rambousky et al., 2013; Rambousky, 2014). The iterative procedure is expensive in terms of computation time. If a low frequency solution is desired, it is usually sufficient to only use the starting values which then lead to position-dependent parameters. No further iteration is required. ${\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{11}}$ and ${\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}$ are calculated using Eq. (38) and then used in Eq. (41), which leads to

$$\begin{array}{}\text{(42)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}^{\star \left(\mathrm{0}\right)}=\left(\begin{array}{cc}\frac{\mathrm{1}}{j\mathit{\omega }}{\mathcal{C}}_{\text{c}}^{\prime -\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}^{-\mathrm{1}}& {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{11}}+\frac{\mathrm{1}}{j\mathit{\omega }}{\underset{\mathrm{¯}}{\mathcal{Z}}}^{\prime }\\ {\underset{\mathrm{¯}}{\mathcal{R}}}_{\mathrm{22}}^{-\mathrm{1}}& \mathbf{0}\end{array}\right).\end{array}$$

An alternative and more efficient method is presented in Sect. 3.2.

3.2 Solution using perturbation theory

The method is based on the direct approximation of the current on a wire. The procedure will initially be described for a single wire and afterwards be extended to multi-wire arrangements. The wire is excited by applying delta sources at one or both ends of the wire. This leads to two linear independent solutions for the potential and the current,

$$\begin{array}{}\text{(43)}& {\displaystyle }\underset{\mathrm{¯}}{\mathit{\varphi }}\left(l\right)=C_{\mathrm{1}}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{1}}\left(l\right)+C_{\mathrm{2}}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{2}}\left(l\right)\end{array}$$

and

$$\begin{array}{}\text{(44)}& {\displaystyle }\underset{\mathrm{¯}}{I}\left(l\right)=C_{\mathrm{1}}{\underset{\mathrm{¯}}{I}}_{\mathrm{1}}\left(l\right)+C_{\mathrm{2}}{\underset{\mathrm{¯}}{I}}_{\mathrm{2}}\left(l\right),\end{array}$$

from which the system of ordinary differential equations (ODEs)

$$\begin{array}{}\text{(45)}& {\displaystyle \frac{\partial }{\partial l}}\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{\varphi }}\\ \underset{\mathrm{¯}}{I}\end{array}\right)+j\mathit{\omega }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{P}}_{\mathrm{11}}\left(l\right)& {\underset{\mathrm{¯}}{P}}_{\mathrm{12}}\left(l\right)\\ {\underset{\mathrm{¯}}{P}}_{\mathrm{21}}\left(l\right)& {\underset{\mathrm{¯}}{P}}_{\mathrm{22}}\left(l\right)\end{array}\right)\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{\varphi }}\\ \underset{\mathrm{¯}}{I}\end{array}\right)=\left(\begin{array}{c}\mathrm{0}\\ \mathrm{0}\end{array}\right),\end{array}$$

can be established (Burg et al., 2013; Heuser, 1995). The entries ${\underset{\mathrm{¯}}{P}}_{ij}$ are continuously differentiable functions for all $l\in [\mathrm{0},\mathrm{1}]$. Employing Eqs. (43) and (44) in Eq. (45), leads to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\partial }{\partial l}}\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{2}}\\ {\underset{\mathrm{¯}}{I}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{I}}_{\mathrm{2}}\end{array}\right)+j\mathit{\omega }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{P}}_{\mathrm{11}}\left(l\right)& {\underset{\mathrm{¯}}{P}}_{\mathrm{12}}\left(l\right)\\ {\underset{\mathrm{¯}}{P}}_{\mathrm{21}}\left(l\right)& {\underset{\mathrm{¯}}{P}}_{\mathrm{22}}\left(l\right)\end{array}\right)\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{2}}\\ {\underset{\mathrm{¯}}{I}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{I}}_{\mathrm{2}}\end{array}\right)\\ \text{(46)}& {\displaystyle }& {\displaystyle }=\left(\begin{array}{cc}\mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}\end{array}\right).\end{array}$$

The coefficients ${\underset{\mathrm{¯}}{P}}_{ij}$ can now be determined as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{P}}_{\mathrm{11}}\left(l\right)& {\underset{\mathrm{¯}}{P}}_{\mathrm{12}}\left(l\right)\\ {\underset{\mathrm{¯}}{P}}_{\mathrm{21}}\left(l\right)& {\underset{\mathrm{¯}}{P}}_{\mathrm{22}}\left(l\right)\end{array}\right)\\ \text{(47)}& {\displaystyle }& {\displaystyle }=-{\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }}}\left(\begin{array}{cc}\frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{1}}& \frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{2}}\\ \frac{\partial }{\partial l}{\underset{\mathrm{¯}}{I}}_{\mathrm{1}}& \frac{\partial }{\partial l}{\underset{\mathrm{¯}}{I}}_{\mathrm{2}}\end{array}\right){\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{2}}\\ {\underset{\mathrm{¯}}{I}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{I}}_{\mathrm{2}}\end{array}\right)}^{-\mathrm{1}},\end{array}$$

under the assumption that the Wronskian exists on the entire domain, i.e. for $\mathrm{0}\le l\le \mathrm{1}$. For a multi-wire problem with N wires, Eq. (45) can be written as

$$\begin{array}{}\text{(48)}& {\displaystyle \frac{\partial }{\partial l}}\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{\varphi }}\\ \underset{\mathrm{¯}}{\mathit{I}}\end{array}\right)+j\mathit{\omega }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{11}}\left(l\right)& {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{12}}\left(l\right)\\ {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{21}}\left(l\right)& {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{22}}\left(l\right)\end{array}\right)\left(\begin{array}{c}\underset{\mathrm{¯}}{\mathit{\varphi }}\\ \underset{\mathrm{¯}}{\mathit{I}}\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right).\end{array}$$

The submatrices ${\underset{\mathrm{¯}}{\mathcal{P}}}_{ij}$ are of dimension N×N, so that the system Eq. (48) is of dimension 2N×2N. In order to compute the coefficients, the derivatives of the currents are required. These are initially approximated using the theory of travelling waves,

$$\begin{array}{}\text{(49)}& {\displaystyle }{\underset{\mathrm{¯}}{I}}_{\mathrm{1}}^{\left(\mathrm{0}\right)}& {\displaystyle }={\underset{\mathrm{¯}}{C}}_{I,\mathrm{1}}{e}^{-jklL},\text{(50)}& {\displaystyle }{\underset{\mathrm{¯}}{I}}_{\mathrm{2}}^{\left(\mathrm{0}\right)}& {\displaystyle }={\underset{\mathrm{¯}}{C}}_{I,\mathrm{2}}{e}^{jklL}.\end{array}$$

Equation (47) can be generalized for N wires as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{2}}\\ {\underset{\mathrm{¯}}{\mathit{I}}}_{\mathrm{1}}^{\left(\mathrm{0}\right)}& {\underset{\mathrm{¯}}{\mathit{I}}}_{\mathrm{2}}^{\left(\mathrm{0}\right)}\end{array}\right)=\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}& {\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}\\ \text{diag}\left(e^{-jkl{L}_j}\right)& \text{diag}\left(e^{jkl{L}_j}\right)\end{array}\right)\\ \text{(51)}& {\displaystyle }& {\displaystyle }\left(\begin{array}{cc}\text{diag}\left({\underset{\mathrm{¯}}{C}}_{I,\mathrm{1}}\right)& \mathbf{0}\\ \mathbf{0}& \text{diag}\left({\underset{\mathrm{¯}}{C}}_{I,\mathrm{2}}\right)\end{array}\right)\end{array}$$

with

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}=\left(\begin{array}{cccc}{\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},\mathrm{11}}& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},\mathrm{12}}& \mathrm{\dots }& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},\mathrm{1}N}\\ {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},\mathrm{21}}& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},\mathrm{22}}& \mathrm{\dots }& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},\mathrm{2}N}\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},N\mathrm{1}}& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},N\mathrm{2}}& \mathrm{\dots }& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{1},NN}\end{array}\right)\text{and}\\ \text{(52)}& {\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}=\left(\begin{array}{cccc}{\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},\mathrm{11}}& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},\mathrm{12}}& \mathrm{\dots }& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},\mathrm{1}N}\\ {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},\mathrm{21}}& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},\mathrm{22}}& \mathrm{\dots }& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},\mathrm{2}N}\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{\ddots }& \mathrm{⋮}\\ {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},N\mathrm{1}}& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},N\mathrm{2}}& \mathrm{\dots }& {\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },\mathrm{2},NN}\end{array}\right),\end{array}$$

where the entries of the matrices are defined as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{f}}_{\mathit{\varphi },m,jp}={\displaystyle \frac{L_p}{c}}{\displaystyle \frac{(-\mathrm{1}{)}^{m-\mathrm{1}}}{{\underset{\mathrm{¯}}{C}}_{m,jp}}}+{\displaystyle \frac{(-\mathrm{1}{)}^m}{c{C}_{\text{c}}^{\prime }}}{e}^{(-\mathrm{1}{)}^{m}jkl{L}_j}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{(-\mathrm{1}{)}^{m-\mathrm{1}}{L}_p}{\mathrm{4}\mathit{\pi }\mathit{\epsilon }c}}\sum _{i=\mathrm{1}}^{N_p}\underset{a_i}{\overset{b_i}{\int }}\left({\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}\right.\\ {\displaystyle }& {\displaystyle }\left.-{\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}\right)e^{(-\mathrm{1}{)}^{m}jk{l}^{\prime }{L}_p}\text{d}{l}^{\prime }\\ \text{(53)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{(-\mathrm{1}{)}^m}{c{C}_{\text{c}}^{\prime }}}{e}^{(-\mathrm{1}{)}^{m}jkl{L}_j}\end{array}$$

for $j,p=\mathrm{1},\mathrm{2},\mathrm{\dots },N$. N_p denotes the number of segments on wire p, m=1 corresponds to the forward travelling wave and m=2 to the backward travelling wave, whereas ${\underset{\mathrm{¯}}{C}}_{m,jp}$ refers to the local capacitance between wires j and p,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{C}}_{m,jp}=\mathrm{4}\mathit{\pi }\mathit{\epsilon }\left(\sum _{i=\mathrm{1}}^{N_p}\underset{a_i}{\overset{b_i}{\int }}\left({\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}\right.\right.\\ \text{(54)}& {\displaystyle }& {\displaystyle }{\left.\left.-{\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}\right)e^{(-\mathrm{1}{)}^{m}jk{l}^{\prime }{L}_p}\text{d}{l}^{\prime }\right)}^{-\mathrm{1}}.\end{array}$$

The matrix containing the derivatives can be established similarly,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}\frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{1}}& \frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathit{\varphi }}}_{\mathrm{2}}\\ \frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathit{I}}}_{\mathrm{1}}^{\left(\mathrm{0}\right)}& \frac{\partial }{\partial l}{\underset{\mathrm{¯}}{\mathit{I}}}_{\mathrm{2}}^{\left(\mathrm{0}\right)}\end{array}\right)=\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{1}}& {\mathcal{G}}_{\mathit{\varphi },\mathrm{2}}\\ -jk\text{diag}\left(L_j{e}^{-jkl{L}_j}\right)& jk\text{diag}\left(L_j{e}^{jkl{L}_j}\right)\end{array}\right)\\ \text{(55)}& {\displaystyle }& {\displaystyle }\left(\begin{array}{cc}\text{diag}\left({\underset{\mathrm{¯}}{C}}_{I,\mathrm{1}}\right)& \mathbf{0}\\ \mathbf{0}& \text{diag}\left({\underset{\mathrm{¯}}{C}}_{I,\mathrm{2}}\right)\end{array}\right),\end{array}$$

where the elements of the submatrices ${\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{1}}$ and ${\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{2}}$ are given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{g}}_{\mathit{\varphi },m,jp}=-j\mathit{\omega }{\underset{\mathrm{¯}}{L}}_{m,jp}-{\underset{\mathrm{¯}}{Z}}^{\prime }{L}_j{e}^{(-\mathrm{1}{)}^{m}jkl{L}_j}\\ {\displaystyle }& {\displaystyle }=-j\mathit{\omega }{\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}{L}_j\sum _{i=\mathrm{1}}^{N_p}\underset{a_i}{\overset{b_i}{\int }}\left({\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}{\mathit{e}}_{t,j}\right(l{L}_j)\\ {\displaystyle }& {\displaystyle }\cdot {\mathit{e}}_{t,p}\left(l^{\prime }{L}_p\right)-{\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}{\mathit{e}}_{t,j}\left(l{L}_j\right)\\ \text{(56)}& {\displaystyle }& {\displaystyle }\cdot {{\mathit{e}}_t}_{\mathrm{1},pi}\left(l^{\prime }{L}_p\right))e^{(-\mathrm{1}{)}^{m}jk{l}^{\prime }{L}_p}{L}_p\text{d}{l}^{\prime }-{\underset{\mathrm{¯}}{Z}}^{\prime }{L}_j{e}^{(-\mathrm{1}{)}^{m}jkl{L}_j}.\end{array}$$

The local inductance between wires j and p is denoted with ${\underset{\mathrm{¯}}{L}}_{m,jp}$ and given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{L}}_{m,jp}={\displaystyle \frac{\mathit{\mu }}{\mathrm{4}\mathit{\pi }}}{L}_j\sum _{i=\mathrm{1}}^{N_p}\underset{a_i}{\overset{b_i}{\int }}\left({\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{pi}(l^{\prime }{L}_p\left)\right|}}{\mathit{e}}_{t,j}\right(l{L}_j)\\ {\displaystyle }& {\displaystyle }\cdot {\mathit{e}}_{t,p}\left(l^{\prime }{L}_p\right)-{\displaystyle \frac{e^{-jk\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}{\left|{\mathit{r}}_j\right(l{L}_j)-{{\mathit{r}}^{\prime }}_{\mathrm{1},pi}(l^{\prime }{L}_p\left)\right|}}{\mathit{e}}_{t,j}\left(l{L}_j\right)\\ \text{(57)}& {\displaystyle }& {\displaystyle }\cdot {{\mathit{e}}_t}_{\mathrm{1},pi}\left(l^{\prime }{L}_p\right))e^{(-\mathrm{1}{)}^{m}jk{l}^{\prime }{L}_p}{L}_p\text{d}{l}^{\prime }.\end{array}$$

The parameter matrix for the N wire problem can as a result be written as

Figure 2 Single wire above ground plane.

Figure 3 Currents at the terminals.

Figure 4 Parameters ${\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{12}}$ and ${\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{21}}$ as function of position.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{11}}^{\left(\mathrm{1}\right)}(l,k)& {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{12}}^{\left(\mathrm{1}\right)}(l,k)\\ {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{21}}^{\left(\mathrm{1}\right)}(l,k)& {\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{22}}^{\left(\mathrm{1}\right)}(l,k)\end{array}\right)=\\ {\displaystyle }& {\displaystyle }{\displaystyle \frac{j}{\mathit{\omega }}}\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{1}}& {\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{2}}\\ -jk\text{diag}\left(L_j{e}^{-jkl{L}_j}\right)& jk\text{diag}\left(L_j{e}^{jkl{L}_j}\right)\end{array}\right)\\ \text{(58)}& {\displaystyle }& {\displaystyle }{\left(\begin{array}{cc}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}& {\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}\\ \text{diag}\left(e^{-jkl{L}_j}\right)& \text{diag}\left(e^{jkl{L}_j}\right)\end{array}\right)}^{-\mathrm{1}}.\end{array}$$

Figure 5 Currents at the terminals in the frequency range from 1 to 50 MHz.

Rewriting the inverse of Eq. (58) following (Bernstein, 2009), allows the parameter matrix to be expressed as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{11}}^{\left(\mathrm{1}\right)}\left(l\right)={\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }}}\left({\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{D}}}_{+}^{\mathrm{2}}-{\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{2}}\right)\\ \text{(59)}& {\displaystyle }& {\displaystyle }{\left({\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}-{\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{D}}}_{+}^{\mathrm{2}}\right)}^{-\mathrm{1}},{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{12}}^{\left(\mathrm{1}\right)}\left(l\right)={\displaystyle \frac{\mathrm{1}}{j\mathit{\omega }}}\left({\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{G}}}_{\mathit{\varphi },\mathrm{2}}-{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}\right)\\ \text{(60)}& {\displaystyle }& {\displaystyle }{\left({\underset{\mathrm{¯}}{\mathcal{D}}}_{+}-{\underset{\mathrm{¯}}{\mathcal{D}}}_{-}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}\right)}^{-\mathrm{1}},\text{(61)}& {\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{21}}^{\left(\mathrm{1}\right)}\left(l\right)=-{\displaystyle \frac{\mathrm{2}}{c}}\text{diag}\left(L_j\right){\underset{\mathrm{¯}}{\mathcal{D}}}_{+}{\left({\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}-{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{D}}}_{+}^{\mathrm{2}}\right)}^{-\mathrm{1}},{\displaystyle }& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{22}}^{\left(\mathrm{1}\right)}\left(l\right)=-{\displaystyle \frac{\mathrm{1}}{c}}\text{diag}\left(L_j\right)\left({\underset{\mathrm{¯}}{\mathcal{D}}}_{-}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}+{\underset{\mathrm{¯}}{\mathcal{D}}}_{+}\right)\\ \text{(62)}& {\displaystyle }& {\displaystyle }{\left({\underset{\mathrm{¯}}{\mathcal{D}}}_{+}-{\underset{\mathrm{¯}}{\mathcal{D}}}_{-}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{1}}^{-\mathrm{1}}{\underset{\mathrm{¯}}{\mathcal{F}}}_{\mathit{\varphi },\mathrm{2}}\right)}^{-\mathrm{1}},\end{array}$$

where

$${\displaystyle }{\displaystyle }\begin{array}{ll}{\underset{\mathrm{¯}}{\mathcal{D}}}_{+}=\text{diag}\left(e^{jkl{L}_j}\right),& {\underset{\mathrm{¯}}{\mathcal{D}}}_{-}=\text{diag}\left(e^{-jkl{L}_j}\right)\\ {\underset{\mathrm{¯}}{\mathcal{D}}}_{+}^{-\mathrm{1}}={\underset{\mathrm{¯}}{\mathcal{D}}}_{-},& {\underset{\mathrm{¯}}{\mathcal{D}}}_{-}^{-\mathrm{1}}={\underset{\mathrm{¯}}{\mathcal{D}}}_{+},\end{array}$$

and

$$\begin{array}{}\text{(63)}& {\displaystyle }{\underset{\mathrm{¯}}{\mathcal{D}}}_{+}^{\mathrm{2}}=\text{diag}\left(e^{j\mathrm{2}kl{L}_j}\right)\end{array}$$

Eq. (45) can be solved employing a fourth order Runge-Kutta algorithm (Steinmetz, 2006). This technique can also be applied to the N wire problem, i.e. Eq. (48). In contrast to the iterative method in Sect. 3.1, the parameters are evaluated without iteration. This considerably reduces the required computation time without compromising the accuracy of the computed results. The Transmission Line Super Theory that is enhanced with the perturbation theory described in this section will henceforth be referred to as TLST/PT.

Figure 6 Two wire configuration.

Figure 7 Currents at the terminals of wire 1.

Figure 8 Currents at the terminals of wire 2.

Only a concentrated excitation has been considered so far. Distributed sources can either be included for symmetric configurations, like a circular loop (Nitsch and Tkachenko, 2005; Tkachenko and Nitsch, 2005), or by direct computation in the TLST. A combination of TLST and TLST/PT is advantageous, since the TLST/PT enables the efficient computation of the parameters. The source terms are iterated in the TLST and then transformed into potential-current representation.

4 Simulated results

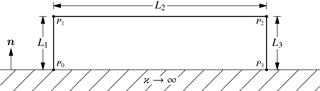
A single wire above a ground plane is considered as a first example. Figure 2 displays the geometry of the wire which consists of three segments.

The segments are of length L_i, $i=\mathrm{1},\mathrm{2},\mathrm{3}$, where segment 1 and 3 are parallel to the normal of the ground plane. The overall length L of the wire is given by the sum ${\sum }_{i=\mathrm{1}}^{\mathrm{3}}{L}_i$. Segment 1 and 2 are connected at point P₁ and segment 2 and 3 at point P₂. The terminals are located at point P₀ and P₃. These points determine the geometry of the wire, where the position vector to a point P_ν is denoted r_ν. In terms of the global parameter l, $\mathrm{0}\le l\le \mathrm{1}$, the position vector to any point on the wire can be written as

$$\begin{array}{}\text{(64)}& {\displaystyle }\mathit{r}\left(l\right)=\left\{\begin{array}{ll}{\mathit{r}}_{\mathrm{0}}+\frac{l-L_{\mathrm{0}}^{\prime }}{L_{\mathrm{1}}^{\prime }-L_{\mathrm{0}}^{\prime }}({\mathit{r}}_{\mathrm{1}}-{\mathit{r}}_{\mathrm{0}}),& L_{\mathrm{0}}^{\prime }\le l<L_{\mathrm{1}}^{\prime }\\ {\mathit{r}}_{\mathrm{1}}+\frac{l-L_{\mathrm{1}}^{\prime }}{L_{\mathrm{2}}^{\prime }-L_{\mathrm{1}}^{\prime }}({\mathit{r}}_{\mathrm{2}}-{\mathit{r}}_{\mathrm{1}}),& L_{\mathrm{1}}^{\prime }\le l<L_{\mathrm{2}}^{\prime }\\ {\mathit{r}}_{\mathrm{2}}+\frac{l-L_{\mathrm{2}}^{\prime }}{L_{\mathrm{3}}^{\prime }-L_{\mathrm{2}}^{\prime }}({\mathit{r}}_{\mathrm{3}}-{\mathit{r}}_{\mathrm{2}}),& L_{\mathrm{3}}^{\prime }\le l\le L_{\mathrm{2}}^{\prime }\end{array}\right.\end{array}$$

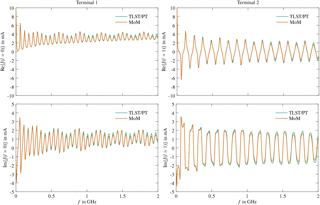
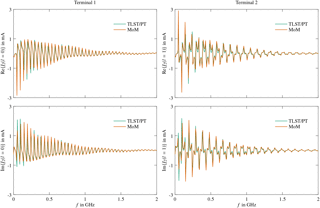
with $L_i^{\prime }={\sum }_{k=\mathrm{1}}^i{L}_k/L$, where $L_{\mathrm{0}}^{\prime }=\mathrm{0}$ and $L_{\mathrm{3}}^{\prime }=\mathrm{1}$. The position vector to a point on an arbitrarily shaped wire consisting of n straight segments can be expressed in the same way. The terminals at point P₀ and P₃ are referred to as terminal 1 and terminal 2, respectively. Figure 3 displays the computed currents at the terminals for a wire with segments of length $L_{\mathrm{1}}=L_{\mathrm{3}}=\mathrm{0.5}$ m and L₂=1.5 m, which implies that segment 2 is parallel to the ground plane. The radius a for the thin wire approximation equals 0.25 mm. Simulations are performed in the frequency range from 1 MHz to 2 GHz, where the transmission line results are computed applying the TLST/PT described in Sect. 3.2. The real and the imaginary parts of the currents at both terminals are in good agreement with method of moment (MoM) results over the entire frequency range which provides a first indication of the accuracy of the computed results. The number of resonances depends on the geometry of the wire and the frequency, since an integer multiple of half of the wavelength must approximately be equal to the length of the wire. This leads to approximately 34 resonances, in good agreement with the simulated results for l=0 in Fig. 3.

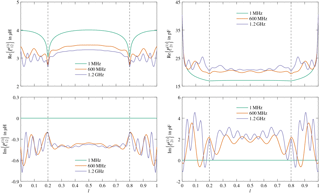
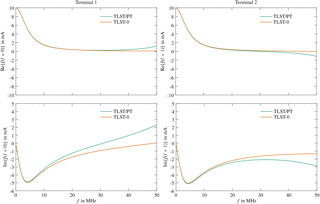
Figure 4 displays the off-diagonal parameters ${\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{12}}$ and ${\underset{\mathrm{¯}}{\mathcal{P}}}_{\mathrm{21}}$. The parameters are dependent on the position and are real-valued in the low frequency case. The graphs clearly show that the imaginary part vanishes along the entire length of the line. The parameters become complex-valued for higher frequencies, where the imaginary part comprises radiation losses. Results for the low frequency case which have been computed using the starting values of the TLST are shown in Fig. 5. The real and imaginary parts at both terminals agree well with the TLST/PT results up to a frequency of approximately 15 MHz.

As a second example, the currents in a two wire configuration in the form of two semicircles is investigated. Analytical solutions are known for a single circular loop (Nitsch and Tkachenko, 2005; Tkachenko and Nitsch, 2005; Storer, 1956; Wu, 1962), and for multiple loops (King and Harrison, 1969), where the solutions are expressed in terms of Fourier series. These solutions are limited to simple wire structures and cannot easily be extended to arbitrary wire configurations. The semicircles considered in this example are of radius R and are separated by a distance d, as shown in Fig. 6. In order to apply the TLST/PT procedure, wire j is discretised with n_j elements, where in this case j is equal to 1 or 2. The terminals of wire j are located at P_j,0 and P_j,n and are referred to as terminal 1 and terminal 2 of wire j, respectively. The four terminals define a rectangle of width 2R and height d, and the two surfaces that are enclosed by the semicircles and the ground plane are both perpendicular to the ground plane. Wire 1 is excited at terminal 1 with the same unit voltage source as in the first example. All remaining terminals are loaded with 50 Ω resistors. Simulations are performed with a semicircle radius R of 1 m, a wire radius a of 0.25 mm, a wire distance d of 0.5 m, and with $n_{\mathrm{1}}=n_{\mathrm{2}}=\mathrm{60}$ segments. Figure 7 shows the currents at the terminals of wire 1 and Fig. 8 the currents at the terminals of wire 2. Good agreement of the TLST/PT and the method of moment results can be observed on all four terminals. This validates the procedure and confirms the applicability of the transmission line procedure with perturbation approach to multi-wire problems.

5 Conclusions

A refined variant of the Transmission Line Super Theory that utilises perturbation theory, and which is referred to as TLST/PT, has been derived and applied to determine currents in thin wire structures. The perturbation approach enables a direct and non-iterative approximation of the initial current in a wire, which reduces the required computation time without compromising the accuracy of the results. The procedure has been applied to compute the currents of a single wire problem and of a two wire configuration. TLST/PT and method of moment results have shown to be in good agreement, which validates the procedure and verifies applicability of the method to multi-wire problems.