Modeling and Simulation of stochastically deformed Waveguides using Schelkunoff's Method

This paper deals with the propagation of electromagnetic waves in cylindrical waveguides with irregularly deformed cross-sections. The general theory of electromagnetic waves is of high interest because of its practical use as a transmission medium. But only in a few special cases, an analytic solution of Maxwell's equations and the appropriate boundary conditions can be found (Spencer, 1951). The coupled-mode theory, also known as Schelkunoff's method, is a semi-numerical method for computing electromagnetic waves in hollow and cylindrical waveguides bounded by perfect electric walls (Saad, 1985). It allows to calculate the transverse field pattern and the propagation constant. The aim of this paper is to derive the so-called generalized telegraphist's equations for irregular deformed waveguides. Subsequently, the method's application will be used on a circular waveguide as an illustrating example.

1 Introduction

Rayleigh was the first to describe the transmission of electromagnetic waves in hollow and perfect conducting waveguides (Rayleigh, 1897). Later on, a general transmission theory of plane electromagnetic waves taking attenuation into account was published by Carson et al. (1936) and Schelkunoff (1937). Since then, the analysis of electromagnetic wave propagation and the practical use of different kinds of waveguides were the subject of intensive research (Southworth, 1950; Miller and Beck, 1953; Miller, 1954a, b). The properties and behavior of electromagnetic waves in hollow, cylindrical waveguides are completely described, when the cutoff frequency and the eigenfunctions are determined. So from a mathematical point-of-view, the problem of electromagnetic wave propagation reduces to determine the solution of Maxwell's equations satisfying the boundary conditions along the waveguide (Schelkunoff, 1952). In fact, only for a few special cross-sections, in which the boundary can be described by an orthogonal coordinate system, the electromagnetic field can be obtained by the method of separating the variables (Stratton, 1941).

However, practical waveguides are usually not uniform in their cross-section due to the manufacturing process. So in case of nonuniform waveguides the method of separation does not work. Schelkunoff (1952, 1955) introduced a more general transmission theory of electromagnetic waves in waveguides by transforming Maxwell's equation into a set of ordinary differential equations. By expanding the electromagnetic field components into an orthogonal series of basis function, an infinite system of differential equation is derived, the so-called generalized telegraphist's equation (GTEs). The approach of the transverse cross-section method is widely used in the analysis of waveguides with varying boundaries (Reiter, 1959; Hung-Chia, 1962; Botton et al., 1998; Zaginaylov et al., 2013).

Based on the earlier work of Schelkunoff (1952, 1955) and Unger (1958, 1961a, c), Maxwell's equation will be converted into generalized telegraphist's equations for an irregular deformed waveguide. Simplifications of the problem were made by modeling the actual boundary of the waveguide by using the so-called impedance boundary condition (IBC) (Senior, 1960).

2 Generalized Telegraphist's Equation

It is well known that the solution of Maxwell's partial differential equation can be reduced to the determination of a vector and a scalar potential. In 1889, Hertz showed that it is possible to define an electromagnetic field with a single vector function (Hertz, 1889). Such a vector function, called the Hertz vector, is simply related to the vector and scalar potential if the region is restricted to an isotropic and homogeneous medium within which are no conduction currents or free electric charges $\left(\mathit{J}=\mathbf{0},\mathit{\rho }=\mathrm{0}\right)$. As a matter of fact, the Hertz vector is only one possible approach. There are two types, the electric and magnetic type (Π_E,Π_M), both satisfying the same vector Helmholtz equation of the form

$$\begin{array}{}\text{(1)}& {\displaystyle }\left(\mathbf{\Delta }+k^{\mathrm{2}}\right)\mathbf{\Pi }=\mathrm{0}.\end{array}$$

In general, the vector Helmholtz Eq. (1) is still too complicated for an analytic solution (Moon and Spencer, 1952). Therefore, it is necessary to take appropriate simplifying steps, so that a particular solution can be easily determined without mathematical difficulties. As common in waveguide analysis, we introduce orthogonal circular curvilinear coordinates $(u,v,z)$, with metrical coefficients $(h_u,h_v,h_z)$. In the case of straight and uniform waveguides, the metrical coefficients of the relevant coordinate system satisfy (Huang and Hung-Chia, 1984)

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial h_u}{\partial z}}=\mathrm{0},{\displaystyle \frac{\partial h_v}{\partial z}}=\mathrm{0}\text{and}{h}_z=\mathrm{1}.\end{array}$$

Thus, in a source free region, the boundary problem is reduced to solving the scalar 2-dimensional Helmholtz equation, which together with the appropriate boundary condition associated with the differential equation is satisfied by the longitudinal component of the Hertz vector

$$\begin{array}{}\text{(3)}& \begin{array}{l}\left.\begin{array}{lc}\left(\mathrm{\Delta }+k_{\mathrm{M}}^{\mathrm{2}}\right){\mathrm{\Pi }}_{\mathrm{M},z}& =\mathrm{0}\\ {\left.{\mathrm{\Pi }}_{\mathrm{M},z}\right|}_{\partial \mathcal{S}}& =\mathrm{0}\end{array}\right\}\text{for TM-modes},\\ \left.\begin{array}{lc}\left(\mathrm{\Delta }+k_{\mathrm{E}}^{\mathrm{2}}\right){\mathrm{\Pi }}_{\mathrm{E},z}& =\mathrm{0}\\ {\left.{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\mathrm{E},z}}{\partial n}}\right|}_{\partial \mathcal{S}}& =\mathrm{0}\end{array}\right\}\text{for TE-modes}.\end{array}\end{array}$$

The reduction of the vector Helmholtz Eq. (1) to the scalar Helmholtz Eq. (3) is a significant step in simplifying the mathematics. For the sake of brevity, we use Π to represent ${\mathrm{\Pi }}_{\mathrm{E},z},{\mathrm{\Pi }}_{\mathrm{M},z}$. In the following we will use the method of separation of variables, we assume

$$\begin{array}{}\text{(4)}& \mathrm{\Pi }(u,v,z)={\mathrm{\Pi }}_{z,\perp }\left(u,v\right)\cdot W\left(z\right)\end{array}$$

where W(z) is a function of the longitudinal coordinate and ${\mathrm{\Pi }}_{\perp }\left(u,v\right)$ a function of the transverse coordinates. The separation of variables yields

$$\begin{array}{}\text{(5)}& {\displaystyle }\left({\mathrm{\Delta }}_{\perp }+k_{\perp }^{\mathrm{2}}\right){\mathrm{\Pi }}_{z,\perp }\left(u,v\right)=\mathrm{0},\left({\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}}{\mathrm{d}{z}^{\mathrm{2}}}}-k_z^{\mathrm{2}}\right)W\left(z\right)=\mathrm{0}\end{array}$$

in which $k_z^{\mathrm{2}}=k^{\mathrm{2}}-k_{\perp }^{\mathrm{2}},k^{\mathrm{2}}:={\mathit{\omega }}^{\mathrm{2}}\mathit{\mu }\mathit{\epsilon }$. It is apparent that the second Eq. (5) has solutions of the form exp (±k_zz), representing forward and backward traveling waves in the longitudinal direction. The transverse pattern of these waves is described independently by the solutions of the 2-dimensional Helmholtz equation. Once Π is found, the electromagnetic field can be derived by simple differentiation according to (Stratton, 1941)

$$\begin{array}{}\text{(6)}& \begin{array}{ll}{\mathit{E}}_{\mathrm{E}}=\left(\mathbf{\Delta }+k_{\mathrm{E}}^{\mathrm{2}}\right){\mathbf{\Pi }}_{\mathrm{E}},& {\mathit{H}}_{\mathrm{E}}=\mathrm{j}\mathit{\omega }\mathit{\epsilon }\mathrm{\nabla }\times {\mathbf{\Pi }}_{\mathrm{E}}\\ {\mathit{E}}_{\mathrm{M}}=-\mathrm{j}\mathit{\omega }\mathit{\mu }\mathrm{\nabla }\times {\mathbf{\Pi }}_{\mathrm{M}},& {\mathit{H}}_{\mathrm{M}}=\left(\mathbf{\Delta }+k_{\mathrm{M}}^{\mathrm{2}}\right){\mathbf{\Pi }}_{\mathrm{M}}\end{array}\end{array}$$

The concept of the so-called generalized telegraphist's equations starts with the separation of the electromagnetic field components and Nabla operator

$$\begin{array}{}\text{(7)}& \begin{array}{ll}\mathit{E}\left(\mathit{r}\right)& ={\mathit{E}}_{⟂}\left(\mathit{r}\right)+E_z\left(\mathit{r}\right){\mathit{e}}_z,\\ \mathit{H}\left(\mathit{r}\right)& ={\mathit{H}}_{⟂}\left(\mathit{r}\right)+H_z\left(\mathit{r}\right){\mathit{e}}_z,\\ \mathrm{\nabla }& ={\mathrm{\nabla }}_{⟂}+{\mathit{e}}_z{\displaystyle \frac{\partial }{\partial z}}\end{array}\end{array}$$

where ${\mathit{E}}_{⟂},{\mathit{H}}_{⟂}$ are the transverse and E_z,H_z are the longitudinal components of the total field. The time dependence exp (−jωt) is omitted. Substituting these fields into the source free Maxwell's equation, we obtain

$$\begin{array}{}\text{(8)}& \begin{array}{l}{\displaystyle \frac{\partial {\mathit{E}}_{⟂}}{\partial z}}=-\mathrm{j}\mathit{\omega }\mathit{\mu }\left({\mathit{H}}_{⟂}\times {\mathit{e}}_z\right)+{\mathrm{\nabla }}_{⟂}{E}_z\\ {\displaystyle \frac{\partial {\mathit{H}}_{⟂}}{\partial z}}=-\mathrm{j}\mathit{\omega }\mathit{\epsilon }\left({\mathit{e}}_z\times {\mathit{E}}_{⟂}\right)+{\mathrm{\nabla }}_{⟂}{H}_z\end{array}\end{array}$$

for the transvers fields and

$$\begin{array}{}\text{(9)}& \begin{array}{l}{E}_z={\displaystyle \frac{\mathrm{1}}{\mathrm{j}\mathit{\omega }\mathit{\epsilon }}}{\mathrm{\nabla }}_{⟂}\cdot \left({\mathit{H}}_{⟂}\times {\mathit{e}}_z\right)\\ H_z={\displaystyle \frac{\mathrm{1}}{\mathrm{j}\mathit{\omega }\mathit{\mu }}}{\mathrm{\nabla }}_{⟂}\cdot \left({\mathit{e}}_z\times {\mathit{E}}_{⟂}\right)\end{array}\end{array}$$

for the longitudinal components. In the next step, the transverse field components will be expanded into series of orthogonal functions of the following form

$$\begin{array}{}\text{(10)}& \begin{array}{l}{\mathit{E}}_{\perp }=\sum _n{V}_{\mathrm{M},n}\left(z\right)\cdot {\mathit{e}}_{\mathrm{M},n}(u,v)+V_{\mathrm{E},n}\left(z\right)\cdot {\mathit{e}}_{\mathrm{E},n}(u,v)\\ {\mathit{H}}_{\perp }=\sum _n{I}_{\mathrm{M},n}\left(z\right)\cdot {\mathit{h}}_{\mathrm{M},n}(u,v)+I_{\mathrm{E},n}\left(z\right)\cdot {\mathit{h}}_{\mathrm{E},n}(u,v)\end{array}\end{array}$$

in which ${\mathit{e}}_{\mathrm{M},n},{\mathit{h}}_{\mathrm{M},n}$ are the vector fields of the eigenmodes of the TM-mode, while those with the index E refer to the eigenmodes of the TE-mode (Reiter, 1959). There are various approaches to the expansion of the electromagnetic field components. A more detailed treatment of the field expansion can be found in the work of Huang and Hung-Chia (1984). The coefficients V_n,I_n are called the complex voltage and current amplitudes. It should be mentioned that the physical dimensions of the coefficients are not those of voltage and current. The eigenmodes are simply related to the previously mentioned Hertz functions (Huang and Hung-Chia, 1984)

$$\begin{array}{}\text{(11)}& {\displaystyle }{\displaystyle }\begin{array}{rl}\text{TM-modes:}{\mathit{e}}_{\mathrm{M},n}& =-{\mathrm{\nabla }}_{\perp }{\mathrm{\Pi }}_{\perp ,\mathrm{M},n}\\ {\mathit{h}}_{\mathrm{M},n}& ={\mathit{e}}_z\times {\mathit{e}}_{\mathrm{M},n}\end{array}\end{array}$$

$$\begin{array}{}\text{(12)}& {\displaystyle }{\displaystyle }\begin{array}{rl}\text{TE-modes:}{\mathit{e}}_{\mathrm{E},n}& ={\mathit{e}}_z\times {\mathrm{\nabla }}_{\perp }{\mathrm{\Pi }}_{\perp ,\mathrm{E},n}\\ {\mathit{h}}_{\mathrm{E},n}& ={\mathit{e}}_z\times {\mathit{e}}_{\mathrm{E},n}.\end{array}\end{array}$$

These vector functions e_n,h_n have certain orthogonality properties which can be expressed as

$$\begin{array}{}\text{(13)}& \begin{array}{l}\underset{\mathcal{S}}{\iint }\left({\mathit{e}}_n\times {\mathit{h}}_m\right)\cdot {\mathit{e}}_z\mathrm{d}S={\mathit{\delta }}_{nm},{\mathit{\delta }}_{nm}=\left\{\begin{array}{lc}\mathrm{1},& n=m\\ \mathrm{0},& n\ne m\end{array}\right.\end{array}\end{array}$$

The Hertz functions of the various modes are determined by Eq. (5) and the boundary conditions Eq. (3) except for arbitrary factors related to the power of the modes. If we choose these constants in such a way that

$$\begin{array}{}\text{(14)}& {\displaystyle }\underset{\mathcal{S}}{\iint }\left(\mathrm{\nabla }{\mathrm{\Pi }}_{⟂}\cdot \mathrm{\nabla }{\mathrm{\Pi }}_{⟂}\right)\mathrm{d}S=k_{⟂}^{\mathrm{2}}\underset{\mathcal{S}}{\iint }{\mathrm{\Pi }}_{⟂}^{\mathrm{2}}\mathrm{d}S=\mathrm{1}\end{array}$$

where S is the cross-section of the waveguide, then the complex power carried by the modes is described by (Schelkunoff, 1952)

$$\begin{array}{}\text{(15)}& {\displaystyle }P={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _n\left(V_{\mathrm{M},n}{I}_{\mathrm{M},n}^{*}+V_{\mathrm{E},n}{I}_{\mathrm{E},n}^{*}\right).\end{array}$$

In this case, the complex voltage and current coefficients correspond to voltages and currents. In order to derive the GTE's, the series expansion Eq. (10) of the transverse field will be substituted into the Eqs. (8) and (9). Subsequently, these equations will be multiplied with orthogonal functions and integrated over the waveguide cross-section 𝒮. Using the orthogonal condition Eq. (13) (Schelkunoff, 1952) and Green's second identity (Schelkunoff, 1951), the GTE's for the basis coeffcients V_n,I_n of the series expansion of the TM- and TE-Modes are derived

$$\begin{array}{}\text{(16)}& {\displaystyle }& {\displaystyle }\begin{array}{l}{\displaystyle \frac{\mathrm{d}{V}_{\mathrm{M},m}}{\mathrm{d}z}}=\sum _n\underset{\partial \mathcal{S}}{\oint }{\left[{\displaystyle \frac{h_v}{h_u}}{E}_{z,n}{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\perp ,\mathrm{M},m}}{\partial u}}\right]}_r\mathrm{d}v\\ +k_{\mathrm{M},m}^{\mathrm{2}}\sum _n\underset{\mathcal{S}}{\iint }{E}_{z,n}{\mathrm{\Pi }}_{\perp ,\mathrm{M},m}\mathrm{d}S-\mathrm{j}\mathit{\omega }\mathit{\mu }{I}_{\mathrm{M},m},\\ {\displaystyle \frac{\mathrm{d}{I}_{\mathrm{E},m}}{\mathrm{d}z}}=\sum _n\underset{\partial \mathcal{S}}{\oint }{\left[{\displaystyle \frac{h_v}{h_u}}{H}_{z,n}{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\perp ,\mathrm{E},m}}{\partial u}}\right]}_r\mathrm{d}v\\ +k_{\mathrm{E},m}^{\mathrm{2}}\sum _n\underset{\mathcal{S}}{\iint }{H}_{z,n}{\mathrm{\Pi }}_{\perp ,\mathrm{E},m}\mathrm{d}S-\mathrm{j}\mathit{\omega }\mathit{\epsilon }{V}_{\mathrm{E},m},\end{array}\text{(17)}& {\displaystyle }& {\displaystyle }\begin{array}{l}{\displaystyle \frac{\mathrm{d}{V}_{\mathrm{E},m}}{\mathrm{d}z}}+\mathrm{j}\mathit{\omega }\mathit{\mu }{I}_{\mathrm{E},m}=\sum _n\underset{\partial \mathcal{S}}{\oint }{\left[E_{z,n}{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\perp ,\mathrm{E},m}}{\partial v}}\right]}_r\mathrm{d}v,\\ {\displaystyle \frac{\mathrm{d}{I}_{\mathrm{M},\mathrm{m}}}{\mathrm{d}z}}+\mathrm{j}\mathit{\omega }\mathit{\epsilon }{V}_{\mathrm{M},m}=\sum _n\underset{\partial \mathcal{S}}{\oint }{\left[{\mathrm{\Pi }}_{\perp ,\mathrm{M},m}{\displaystyle \frac{\partial H_{z,n}}{\partial v}}\right]}_r\mathrm{d}v.\end{array}\end{array}$$

The set of GTE's is equivalent to the equations in Unger (1961b). A more detailed derivation of the equation above can be found in Weiss and Mathis (1998). For a further analysis of the GTE's, the field components in the integral kernel of the line integral need to be determined.

2.1 Boundary Conditions

There are different kinds of boundary conditions to model the actual boundary of a waveguide. One of the most commonly used boundary conditions is the perfect electric conductor (PEC)

$$\begin{array}{}\text{(18)}& {\displaystyle }\mathit{n}\times \mathit{E}=\mathbf{0},\mathit{n}\cdot \mathit{B}=\mathrm{0},\mathit{n}={\displaystyle \frac{\frac{\partial \mathit{r}}{\partial \mathit{\varphi }}\times \frac{\partial \mathit{r}}{\partial z}}{\left|\frac{\partial \mathit{r}}{\partial \mathit{\varphi }}\times \frac{\partial \mathit{r}}{\partial z}\right|}}.\end{array}$$

where n is the outward unit normal vector to the boundary ∂𝒮. In case of a circular waveguide, we obtain of Eq. (18) for the tangential electric and normal magnetic components

$$\begin{array}{}\text{(19)}& {\displaystyle }{\left.E_{\mathit{\varphi }}\right|}_{\partial \mathcal{S}}=\mathrm{0},{\left.E_z\right|}_{\partial \mathcal{S}}=\mathrm{0}\text{and}{\left.B_r\right|}_{\partial \mathcal{S}}=\mathrm{0}.\end{array}$$

The equations above specify the relations which must be satisfied by the electric and magnetic field at the boundary ∂𝒮.

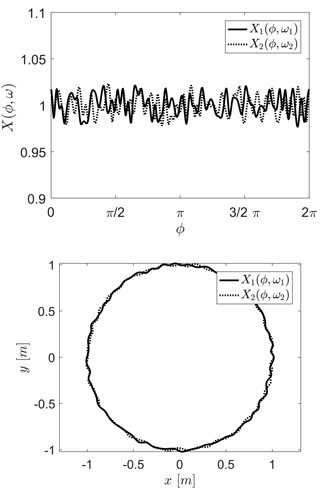
In case of small irregular deformations of the cross-section, it is appropriate to use the perturbation theory. The surface of the waveguide can be represented in cylindrical coordinates $\left(r,\mathit{\varphi },z\right)$. The radius r of the cross-section is a function of ϕ,z and a parameter ω

$$\begin{array}{}\text{(20)}& {\displaystyle }r\left(\mathit{\xi }\left(\mathit{\varphi },z,\mathit{\omega }\right)\right)=r_{\mathrm{0}}\cdot \left(\mathrm{1}+\mathit{\xi }\left(\mathit{\varphi },z,\mathit{\omega }\right)\right),\end{array}$$

where r₀ is the waveguide mean radius and the function ξ describes the irregular deformation of the cross-section. For convenience the deformation function ξ will only be a function of ϕ and ω. So instead of the usual boundary conditions Eq. (19), the field components have additional terms

$$\begin{array}{}\text{(21)}& {\displaystyle }{E}_{\mathit{\varphi }}=\mathrm{0},E_z={\displaystyle \frac{\partial r(\mathit{\varphi },\mathit{\omega })}{\partial \mathit{\varphi }}}{E}_r\text{and}{B}_r={\displaystyle \frac{\partial r(\mathit{\varphi },\mathit{\omega })}{\partial \mathit{\varphi }}}{B}_{\mathit{\varphi }}.\end{array}$$

The next task is to express the field components at a mean surface r₀ (regular boundary) and this is done by expanding the field components in a Taylor series in ξ (Senior, 1960; Unger, 1961a). Since the field is finite and continuous within the boundary, we have the following form

$$\begin{array}{}\text{(22)}& \begin{array}{ll}{E}_{\mathit{\varphi }}(r\left(\mathit{\xi }\right),\mathit{\varphi })& =E_{\mathit{\varphi }}(r_{\mathrm{0}},\mathit{\varphi })+r_{\mathrm{0}}\mathit{\xi }{\displaystyle \frac{\partial }{\partial r}}{E}_{\mathit{\varphi }}(r_{\mathrm{0}},\mathit{\varphi })\\ & +r_{\mathrm{0}}^{\mathrm{2}}{\displaystyle \frac{{\mathit{\xi }}^{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{{\partial }^{\mathrm{2}}}{\partial r^{\mathrm{2}}}}{E}_{\mathit{\varphi }}(r_{\mathrm{0}},\mathit{\varphi })+\mathrm{\dots },\end{array}\end{array}$$

where the differentiation must be carried out before r is put equal to r₀. In this paper, we will use the first order approximation of the boundary condition and all higher order terms will be neglected (Unger, 1961a). Substituting the Taylor series into Eq. (21), we obtain

$$\begin{array}{}\text{(23)}& \begin{array}{ll}{\left.E_{\mathit{\varphi }}\right|}_{\partial \mathcal{S}}& =-r_{\mathrm{0}}\mathit{\xi }{\displaystyle \frac{\partial E_{\mathit{\varphi }}}{\partial r}},\\ {\left.E_z\right|}_{\partial \mathcal{S}}& ={\displaystyle \frac{\partial r(\mathit{\varphi },\mathit{\xi })}{\partial \mathit{\varphi }}}\left(E_r+r_{\mathrm{0}}\mathit{\xi }{\displaystyle \frac{\partial E_r}{\partial r}}\right)-r_{\mathrm{0}}\mathit{\xi }{\displaystyle \frac{\partial E_z}{\partial r}},\\ {\left.B_r\right|}_{\partial \mathcal{S}}& ={\displaystyle \frac{\partial r(\mathit{\varphi },\mathit{\xi })}{\partial \mathit{\varphi }}}\left(B_{\mathit{\varphi }}+r_{\mathrm{0}}\mathit{\xi }{\displaystyle \frac{\partial B_{\mathit{\varphi }}}{\partial r}}\right)-r_{\mathrm{0}}\mathit{\xi }{\displaystyle \frac{\partial B_r}{\partial r}}.\end{array}\end{array}$$

For a more general approach the IBC will be used (Katsenelenbaum, 1998)

$$\begin{array}{}\text{(24)}& \mathit{n}\times \mathit{E}=Z\cdot \mathit{n}\times \left(\mathit{n}\times \mathit{H}\right),Z={\displaystyle \frac{k}{\mathit{\kappa }-\mathrm{j}\mathit{\mu }\mathit{\epsilon }}}.\end{array}$$

It can be shown that the PEC Eq. (18) is only a special case of the IBC Eq. (24) (Z=0). Using the same method as above, we obtain two equations for the tangential electric field components

$$\begin{array}{}\text{(25)}& \begin{array}{ll}{E}_z& =Z\cdot \left(H_{\mathit{\varphi }}+{\displaystyle \frac{\partial r(\mathit{\varphi },\mathit{\xi })}{\partial \mathit{\varphi }}}{H}_r\right),\\ E_{\mathit{\varphi }}& =-Z\left(H_z+{\left({\displaystyle \frac{\partial r(\mathit{\varphi },\mathit{\xi })}{\partial \mathit{\varphi }}}\right)}^{\mathrm{2}}{H}_z\right)-{\displaystyle \frac{\partial r(\mathit{\varphi },\mathit{\xi })}{\partial \mathit{\varphi }}}{E}_{\mathit{\varphi }},\end{array}\end{array}$$

which can be substituted in the line integral of Eqs. (16) and (17).

Figure 1 X₁(ϕ,ω₁) and X₂(ϕ,ω₂) are two realizations of the stochastic process. Parameters for simulations: N=60, r₀=1 and ${\mathit{\delta }}_{max}=\mathrm{1}$.

2.2 Stochastic Process

In the previous section, the boundary condition for an irregular deformed waveguide was modeled. The imperfections on the surface ∂S, where we assume that there is no rule for these deformations, were described by the function ξ(ϕ,ω). Therefore, it is useful to interpret the perturbation term ξ as a random variable X(ϕ,ω). For this purpose, an appropriate probability space $(\mathrm{\Omega },\mathcal{A},P)$ with a sample space Ω, a σ-algebra 𝒜 and a probability measure P has to be constructed where ω∈Ω (Mathis and Mathis, 2015). For computational and mathematical reasons, the stochastic process has the following form

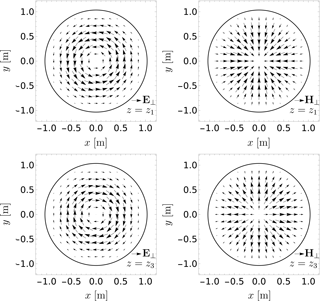
Figure 2 Change of transverse field pattern of the electric and magnetic field along the z-axis.Parameters for simulation: N=60, r₀=1 and ${\mathit{\delta }}_{max}=\mathrm{0.1}$.

Table 1 Coupling modes in the irregularly deformed waveguide.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }X\left(\mathit{\varphi },\mathit{\omega }\right)=\\ \text{(26)}& {\displaystyle }& {\displaystyle }\begin{array}{l}\left\{\begin{array}{lcl}{\mathit{\xi }}_{\mathrm{1}}\left(\mathit{\varphi },\mathit{\omega }\right),& \mathrm{0}\le \mathit{\varphi }\le {\displaystyle \frac{\mathrm{2}\mathit{\pi }}{N}},& \mathit{\omega }\in \mathrm{\Omega }\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}\\ {\mathit{\xi }}_n\left(\mathit{\varphi },\mathit{\omega }\right)& {\displaystyle \frac{\mathrm{2}\mathit{\pi }\left(n-\mathrm{1}\right)}{N}}<\mathit{\varphi }\le {\displaystyle \frac{\mathrm{2}\mathit{\pi }n}{N}}& \mathit{\omega }\in \mathrm{\Omega }\\ \mathrm{⋮}& \mathrm{⋮}& \mathrm{⋮}\\ {\mathit{\xi }}_N\left(\mathit{\varphi },\mathit{\omega }\right),& {\displaystyle \frac{\mathrm{2}\mathit{\pi }\left(N-\mathrm{1}\right)}{N}}<\mathit{\varphi }\le \mathrm{2}\mathit{\pi },& \mathit{\omega }\in \mathrm{\Omega }\end{array}\right.\end{array}\end{array}$$

with

$${\mathit{\xi }}_n=c_{n,\mathrm{3}}\left(\mathit{\omega }\right)\cdot {\mathit{\varphi }}^{\mathrm{3}}+c_{n,\mathrm{2}}\left(\mathit{\omega }\right)\cdot {\mathit{\varphi }}^{\mathrm{2}}+c_{n,\mathrm{1}}\left(\mathit{\omega }\right)\cdot \mathit{\varphi }+c_{n,\mathrm{0}}\left(\mathit{\omega }\right).$$

With this specific form of the stochastic process X(ϕ,ω), the randomness is contained in the coefficients c_n,i(ω) of the polynomial and can be separated from the variable ϕ. So the line integral in Eqs. (16)–(17) can be evaluated before the stochastic integration. Due to this form, there is a computational advantage in calculating the coupling coefficients. As an illustrating example, two realizations of the stochastic process X(ϕ,ω) are shown in Fig. 1.

Figure 3 Change of transverse field pattern of the electric and magnetic field along the z-axis. Parameters for simulation: N=60, r₀=1 and ${\mathit{\delta }}_{max}=\mathrm{1}$.

3 Numeric Results

In this section, we will present the method of computing the stochastic GTE's. After substituting the field components of the IBC Eq. (25) into each integrand of the line integrals of Eqs. (16) and (17), the coupling coefficients on the right side of the equations will be divided into a deterministic and stochastic part. Combining the Eqs. (16) and (17) into the form of state space equations we obtain

Figure 4 All the basis coefficients V_E,n and I_E,n. Parameters for simulation: N=60, r₀=1 and ${\mathit{\delta }}_{max}=\mathrm{1}$.

Table 2 Parameters for simulation of excited TE₀₁-mode.

$$\begin{array}{}\text{(27)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}\mathit{x}}{\mathrm{d}z}}=\underset{\mathrm{¯}}{\mathbf{D}}\cdot \mathit{x}+\underset{\mathrm{¯}}{\mathbf{S}}\left(\mathit{\omega }\right)\cdot \mathit{x}\mathrm{with}\mathit{x}=\left[\begin{array}{c}{\mathit{V}}_{\mathrm{M}}\\ {\mathit{I}}_{\mathrm{M}}\\ {\mathit{V}}_{\mathrm{E}}\\ {\mathit{I}}_{\mathrm{E}}\end{array}\right]\text{(28)}& {\displaystyle }& {\displaystyle }\begin{array}{ll}\underset{\mathrm{¯}}{\mathbf{D}}=& \left[\begin{array}{cccc}{\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{0}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{1}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{2}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{3}}\\ {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{4}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{5}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{6}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{7}}\\ {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{8}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{9}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_a& {\underset{\mathrm{¯}}{\mathbf{D}}}_b\\ {\underset{\mathrm{¯}}{\mathbf{D}}}_c& {\underset{\mathrm{¯}}{\mathbf{D}}}_d& {\underset{\mathrm{¯}}{\mathbf{D}}}_e& {\underset{\mathrm{¯}}{\mathbf{D}}}_f\end{array}\right],\\ & \\ \underset{\mathrm{¯}}{\mathbf{S}}\left(\mathit{\omega }\right)=& \left[\begin{array}{cccc}{\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{0}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{1}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{2}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{3}}\left(\mathit{\omega }\right)\\ {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{4}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{5}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{6}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{7}}\left(\mathit{\omega }\right)\\ {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{8}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{9}}\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_a\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_b\left(\mathit{\omega }\right)\\ {\underset{\mathrm{¯}}{\mathbf{S}}}_c\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_d\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_e\left(\mathit{\omega }\right)& {\underset{\mathrm{¯}}{\mathbf{S}}}_f\left(\mathit{\omega }\right)\end{array}\right].\end{array}\end{array}$$

The next task is to consider all couplings between the different modes (see Table 1). For convenience, the double subscription for the designation of various modes has been substituted by a single subscription, but in order to consider all possible couplings the double subcription is useful. We will substitute the single subscription n and m with the double subscription [pq] and [rs]

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }n=\left[pq\right]m=\left[rs\right],p,r=\mathrm{0},\mathrm{1}\mathrm{\dots },q,s=\mathrm{1},\mathrm{2}\mathrm{\dots }.\\ \text{(29)}& {\displaystyle }& {\displaystyle }\mathit{V}=\left[\begin{array}{c}{V}_{\mathrm{01}}\\ V_{\mathrm{11}}\\ V_{\mathrm{02}}\\ V_{\mathrm{12}}\end{array}\right],{\underset{\mathrm{¯}}{\mathbf{S}}}_i\left(\mathit{\omega }\right)=\left[\begin{array}{c}{S}_{i,\mathrm{0101}}{S}_{i,\mathrm{0111}}{S}_{i,\mathrm{0102}}{S}_{i,\mathrm{0112}}\\ S_{i,\mathrm{1101}}{S}_{i,\mathrm{1111}}{S}_{i,\mathrm{1102}}{S}_{i,\mathrm{1112}}\\ S_{i,\mathrm{0201}}{S}_{i,\mathrm{0211}}{S}_{i,\mathrm{0202}}{S}_{i,\mathrm{0212}}\\ S_{i,\mathrm{1201}}{S}_{i,\mathrm{1211}}{S}_{i,\mathrm{1202}}{S}_{i,\mathrm{1212}}\end{array}\right].\end{array}$$

In the case of the introduced stochastic process X(ϕ,ω) (Eq. 26), the matrices $\underset{\mathrm{¯}}{\mathbf{D}}$ and $\underset{\mathrm{¯}}{\mathbf{S}}$ (Eq. 28) become sparse matrices

$$\begin{array}{}\text{(30)}& {\displaystyle }\begin{array}{ll}\underset{\mathrm{¯}}{\mathbf{D}}& =\left[\begin{array}{cccc}\underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{1}}& \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{3}}\\ \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}\\ \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_{\mathrm{9}}& \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_b\\ \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{D}}}_e& \underset{\mathrm{¯}}{\mathbf{0}}\end{array}\right],\\ & \\ \underset{\mathrm{¯}}{\mathbf{S}}\left(\mathit{\omega }\right)& =\left[\begin{array}{cccc}\underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{1}}\left(\mathit{\omega }\right)& \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{3}}\left(\mathit{\omega }\right)\\ \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}\\ \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{S}}}_{\mathrm{9}}\left(\mathit{\omega }\right)& \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{S}}}_b\left(\mathit{\omega }\right)\\ \underset{\mathrm{¯}}{\mathbf{0}}& \underset{\mathrm{¯}}{\mathbf{0}}& {\underset{\mathrm{¯}}{\mathbf{S}}}_e\left(\mathit{\omega }\right)& \underset{\mathrm{¯}}{\mathbf{0}}\end{array}\right].\end{array}\end{array}$$

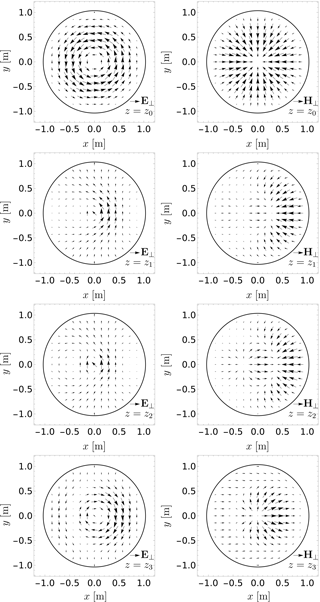
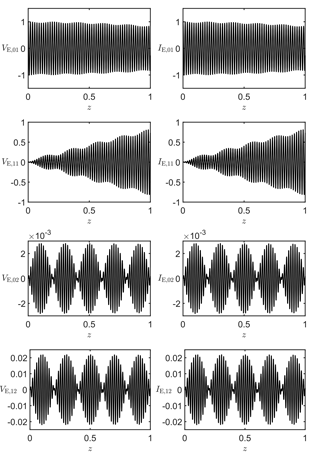
As an example, we will calculate the basis coefficients V_n,I_n for an excited TE₀₁-mode. The simulation parameters are shown in Table 2. δ_max describes the maximum deviation from the mean radius r₀, while z_i characterizes four different cross-sections of the waveguide. The associated voltage and currents coefficients V_n,I_n are shown in Fig. 4. In Fig. 3, there are the transverse patterns of the electric and magnetic field at four different cross-sections. There are obvious changes of the transverse pattern due to the variation of the radius (see Fig. 1). In the case of a TE₀₁-mode, the electric and magnetic field components are

$$\begin{array}{}\text{(31)}& {\displaystyle }{E}_r=\mathrm{0},E_{\mathit{\varphi }}\ne \mathrm{0},E_z\ne \mathrm{0}{H}_r\ne \mathrm{0},H_{\mathit{\varphi }}=\mathrm{0},H_z=\mathrm{0}.\end{array}$$

The deformation causes other field components to arise, which can be seen in the changes of the transverse pattern of the electric and magnetic field (see Fig. 3). According to the results of the simulation for the voltage and current coefficients, there is an attenuation to V_M,01 and I_M,01, besides the excited TE₀₁-mode there are other spurious modes (see Fig. 4). If the maximal deviation become less than 0.1 % of the mean radius r₀, the transverse pattern of the electric and magnetic field show no significant changes along the propagation direction (see Fig. 2). It is also important to mention that the impedance factor Z (Eq. 24) is restricted to small values close to Z=0 (Botton et al., 1998; Vlasov and Antonsen, 2001). The effect of mode conversion and attenuation of the excited wave will not be discussed in this work and need further investigation.

4 Conclusions

In this paper it was shown, that it is possible to derive stochastic generalized telegraphist's equation for irregular deformed waveguides for a specific random process. In the case of the impedance boundary condition from Leontovich (IBC), the mathematical derivation and first numeric results were presented. The changes of the transverse field pattern of a circular electric wave (TE₀₁) in the direction of propagation was determined. Effects of mode conversion and attenuation due to the surface roughness and finite conductivity need further investigation. Especially, the choice of the model of the boundary condition as well as the stochastic process is essential. In consequence of non-uniform convergence of the basis function, the impedance has to be close to zero (Botton et al., 1998). In a recent work from Zaginaylov and Shcherbinin (2016) a new approach was given for that problem.