A machine learning joint lidar and radar classification system in urban automotive scenarios
Falk Schubert
Ralph Rasshofer
Erwin Biebl
This work presents an approach to classify road users as pedestrians, cyclists or cars using a lidar sensor and a radar sensor. The lidar is used to detect moving road users in the surroundings of the car. A 2-dimensional range-Doppler window, a so called region of interest, of the radar power spectrum centered at the object's position is cut out and fed into a convolutional neural network to be classified. With this approach it is possible to classify multiple moving objects within a single radar measurement frame. The convolutional neural network is trained using data gathered with a test vehicle in real urban scenarios. An overall classification accuracy as high as 0.91 is achieved with this approach. The accuracy can be improved to 0.94 after applying a discrete Bayes filter on top of the classifier.
- Article
(4120 KB) - Full-text XML
- BibTeX
- EndNote
On the road to highly and fully automated driving, modern cars need to not only capture their environment, but also be able to understand it. For this purpose, being able to classify the type of objects in the cars' surroundings is of major importance. This is especially true on inner city roads where the everyday traffic situation is very complex and highly dynamic, due to multiple kinds of users, such as pedestrians, bicycles and cars, sharing the road. Pedestrians and cyclists are particularly prone to sustain a serious injury when involved in a traffic accident and thus belong to the vulnerable road users group.
While the overall number of fatalities from the vulnerable road users group in the European Union decreased between 2006 and 2015, they still made up in 2015 for 21 % (5435 pedestrians) and 7,8 % (2043 cyclists) of all road accident fatalities (European Commission, 2017a, b). This makes capturing and understanding the cars' surroundings in urban scenarios of utmost importance.
A variety of sensors is integrated in modern cars for this purpose. Two of the most important ones are lidar and radar systems, both with advantages and shortcomings. While a lidar sensor has excellent range and angular resolution, it can only measure velocity by differentiating over position measurements. On the other hand, a radar sensor is outperformed in position measurements, but it is able to measure relative velocities directly by means of the Doppler effect. With modern radar sensors it is even possible to measure the motion of the single components of a moving body. These motions' components are known as the micro-Doppler (Chen et al., 2006) of a radar signal and carry additional information about the type of object, which can be used for classification.
Machine learning algorithms are well suited for classification tasks. They have gained significant traction in the computer vision world due to the availability of increasingly large data sets and the rapid development of hardware for parallel computing. In the domain of radar signal processing, machine learning has had an impact as well, e.g. for fall detection (Jokanovic et al., 2016) or for unmanned aerial systems detection and classification (Mendis et al., 2016). In the automotive industry, machine learning has also been of great interest in combination with the micro-Doppler effect as a way of classifying different subjects (e.g., Pérez et al., 2018; Prophet et al., 2018; Heuel and Rohling, 2012). In Pérez et al. (2018) a radar-based classification system which works on a single-frame basis was introduced. While it showed that classification based on the radar range-Doppler-angle power spectrum was possible, the approach was nonetheless limited to single target scenarios and thus not entirely suitable for urban automotive scenarios.
Another promising approach with origin in the image classification and detection domain is that of semantic segmentation, where each pixel in an image is assigned a class probability vector. Schumann et al. (2018) used an adapted version of PointNet++ (Qi et al., 2017) for semantic segmentation on four-dimensional (two spatial coordinates, compensated Doppler velocity and radar cross section) radar point clouds. The radar point clouds are obtained performing a constant false alarm rate (CFAR) detection procedure. This kind of approach has the advantage of avoiding both the clustering of detections and the manual selection of feature vectors.
This work presents a machine learning classification system for urban automotive scenarios using a lidar and a radar sensor. Here, a different approach was chosen, where the input of the classification network is a region of interest (ROI) of the range-Doppler-angle spectrum, without applying a detection procedure, such as CFAR, beforehand. By doing so, the discarding of possible valuable information, e.g. micro-Doppler components, by the detection algorithm is avoided. The system classifies the detected objects as either pedestrians, cyclists, cars or noise (i.e. no object present). In order to lay the focus on the classification performance, the lidar was chosen instead of the radar for the detection of the ROIs, since reliable detection and tracking algorithms were already implemented in the test-vehicle.
The remaining of the paper is structured as follows. In Sect. 2 the general principle of the detection and classification system is introduced. Section 2.1 describes in detail the architecture of the convolutional neural network (CNN), which is used to perform the classifications. Section 3 goes into the details of the test vehicle used to gather the data sets and into the training of the CNN. The results of the proposed approach as well as a high level tracking filter to improve the performance are presented in Sect. 4. The conclusions of this work and an outlook for future work are laid out in Sect. 5.
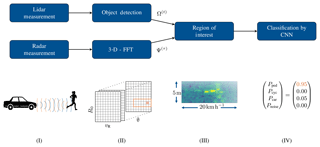
Figure 1Description of the classification system. At stage I both radar and lidar measurements are performed (asynchronous). Stage II provides the lidar object list Ω(t) and the processed radar measurement Ψ(τ), which contains the range-Doppler-angle power spectrum. Using the timestamps, the measurements are matched at stage III and the ROIs are extracted from the power spectrum. At stage IV the ROIs are classified by the CNN.
The concept of the classification system is depicted in Fig. 1. On the one hand, the lidar sensor is responsible for detecting objects and tracking them over time. It delivers at each time step t an object list Ω(t). A single object within Ω(t) is described by the tuple
where idk is an identification number given to the k-th object, tsk a time stamp of the measurement, xk and yk the estimated position (middle point of the estimated bounding box) in the car's coordinate system, and vx,k and vy,k the velocities in x and y direction.
On the other hand, the radar system is responsible for the object classification task. It is a chirp sequence frequency-modulated continuous wave radar with 8 receive channels. The channels are arranged as a uniform linear array in azimuth direction with neighboring elements separated by half a wavelength at 77 GHz. The back-scattered, down-converted, sampled signal at the receiver can be modeled by
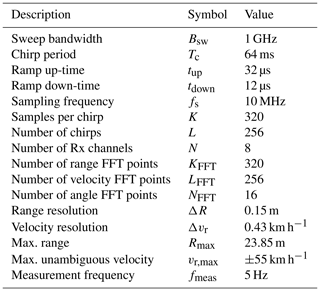
with k the sample index within one chirp, l the chirp index, u the receiver index, fB the beat frequency, fD the Doppler frequency, fθ the normalized spatial frequency, fs the sampling frequency and Tc the chirp period (Pérez et al., 2018). By applying 3 independent fast Fourier transforms (FFTs) across the k, l and u axis the range-Doppler-angle spectrum is obtained. This allows to resolve objects in range, velocity and angle dimensions, depending on the system parameters shown in Table 1.
A radar measurement at time step τ is composed of the tuple
where PB denotes the range-Doppler-angle power spectrum and “ts” the time stamp of the radar measurement.
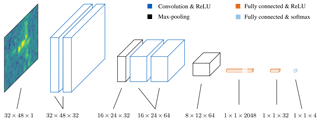
Figure 2Convolutional neural network architecture based on the VGGNet architecture from Simonyan and Zisserman (2014).
Since the lidar and radar measurements are not triggered by a common source, the measurements need to be matched to one another using their time stamps. The radar measurement frequency fmeas is the lower one and thus for each radar measurement a lidar measurement that best matches the radar's time stamp is selected.
After building a radar-lidar measurement pair, all the objects in Ω(t) – excluding those outside the radar's field of view – are mapped to a location within the range-Doppler-angle power spectrum. This is achieved by converting an objects' spatial coordinates (xk and yk) to a range R0,k and azimuth angle θk in the radar's coordinate system. In the same way, an object's radial velocity vR,k and thus Doppler frequency is computed from its velocity components (vx,k and vy,k) provided by the lidar. A 2-dimensional region of interest (ROI) centered at (R0,k, vR,k) in range and Doppler dimensions is then extracted from at the azimuth angle bin nearest to θk (see Fig. 1 – III). The ROI is rectangular in shape and has a fixed size of . This size was chosen to fit the range-Doppler signatures of pedestrians, bicycles and cars, while keeping it as small as possible.
Finally, the ROIs are fed to the convolutional neural network, which will be further explained in Sect. 2.1. The CNN computes the class probability vectors and a decision is made in favor of the class with the highest probability.
2.1 Convolutional neural network architecture
The architecture of the CNN, depicted in Fig. 2, is based on the VGGNet network (Simonyan and Zisserman, 2014). In the convolutional layers, only filters of size 3×3 are used. These filters are all slid with a stride of 1 and zero-padding is applied to the edges of the input maps to preserve the same dimensions at the output. The convolutional layers come in groups of 2 followed by a max-pooling operation. The receptive field of the max-pooling filters has a size of 2×2, which means that at the output of the pooling layers the feature maps get reduced by a factor of 4. After the second group of convolutional layers, three fully connected layers follow which progressively get smaller in size.
Every convolutional and fully connected layer (except for the last one) is followed by an activation function – the rectified linear unit (ReLU). The ReLU is defined as and it introduces a nonlinear behavior to the network. At the last stage a softmax function turns the logits into the class probabilities by fitting them between 0 and 1 and ensuring that their sum adds up to 1.
To perform the measurements and acquire the data a test vehicle was used. The vehicle is a BMW 5 Series (F10) equipped with a variety of sensors. For this work only the radar, the front lidar and the front camera are of relevance (see Fig. 3). The radar system was fitted within the right kidney grill using a specially designed case. The front camera, mounted in place of the rear-view mirror, is exclusively used as an aid to label the radar data.

Figure 3Test vehicle (BMW 5 Series F10) equipped with radar (Radarbook from INRAS), lidar and camera sensors. Photograph source: [Authors].
The data was gathered by driving in the surrounding area of the Technical University of Munich. This resulted in a varied number of scenarios in real urban settings, i.e. subjects from all classes in a varied range of directions (both lateral and longitudinal with respect to the radar's orientation). All measurements were performed during daytime with no precipitation present.
In order to process the dataset the ROIs given by the lidar object lists were labeled semi-automatically and all frames were controlled and, if necessary, corrected manually. Since the classification approach produces one prediction per ROI, only tracks with one target present or with a clear dominant target within the ROI were selected. Figure 4 depicts an example measurement frame with the ROI enclosed by a red rectangle (upper half). The lower half of Fig. 4 displays the front camera picture, that shows a cyclist corresponding to the ROI.
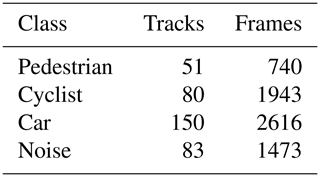
The distribution of the training dataset can be taken from Table 2. A track Tid is composed of an arbitrary number of frames Z, which belong to the same object Oid:
where “id” stands for the object's identification number (see Eq. 1). In order to create the noise tracks, regions of the range-Doppler-angle power spectrum without any targets present were manually sampled. It is worth noting, that the car class includes larger vehicles, such as trucks, as well.
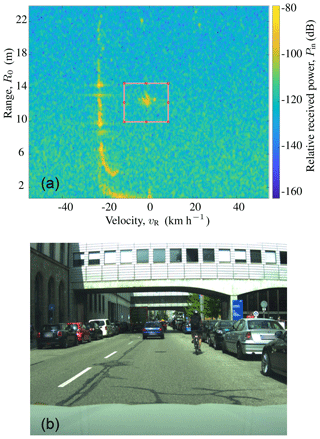
Figure 4Example of a measurement frame with a cyclist in the radar's FOV. The top half shows the range-Doppler-angle power spectrum PB for a fixed angle with the ROI used for classification marked in red. The front camera picture is shown on the bottom half. Photograph source: [Authors].
The network was implemented with help of the TensorFlow software library (Abadi et al., 2015). Since the network is not particularly deep and the convolution filters are also quite small, training is not very time consuming. Using a NVIDIA GeForce GTX 1080 Ti GPU, the time it takes to train the CNN is only around 2 min. At test time, a single inference takes less than 2 ms (without taking into consideration any of the radar signal processing).
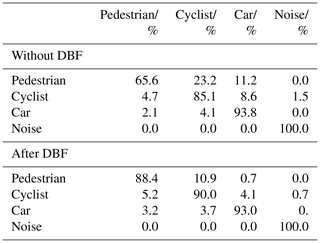
Table 4Confusion matrix for data set from Table 3 before (top) and after (bottom) DBF.
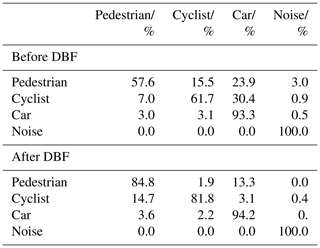
Table 5Precision and recall for data set from Table 3 before (top) and after (bottom) DBF.
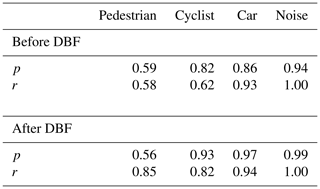
The top half of Table 4 shows the confusion matrix that results after running the data set from Table 3 through the convolutional neural network. Two common metrics to assess the performance of a classifier are the precision and the recall. The precision is defined as
where “tp” is the number of true positives and “fp” the number of false positives. It relates the number of correct predictions (tp) to the number of overall positive predictions (tp+fp) for a given class. On the other hand, the recall, or sensitivity, gives the fraction of a class that gets correctly classified and it is defined as
where “fn” is the number of false negatives (Shalev-Shwartz and Ben-David, 2014, p. 244).
From both the precision and the recall it can be seen that the classification network has trouble with the pedestrian class. A glance at the confusion matrix (top half of Table 4) shows that pedestrians tend to be confused with both cyclists and cars. While the classifier performs better for cyclists, about a third of all cyclist frames get wrongfully classified as cars. The car and noise classes show an overall good performance with the car class having just a small percentage misclassified as either pedestrians or cars. The overall classification accuracy for this data set is 0.84.
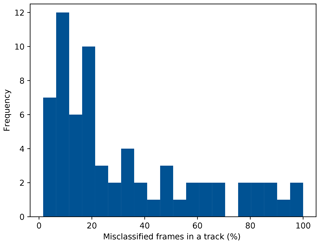
Figure 5Histogram of the relative number of erroneously classified frames per track. Tracks without any misclassified frames are not included.
A further analysis of the results shows, that many classification errors occur for only a small number of frames within a track. Figure 5 depicts a histogram of the relative number of errors per track (excluding tracks without errors). From the histogram it can be observed, that tracks with a low percentage of misclassified frames are more frequent than tracks with a high percentage of misclassified frames.
Nonetheless, there are still tracks where the system fails to correctly classify the majority of the frames (15 out of 114 tracks). One common occurrence that can be observed within some of these tracks (5 out of 15) is multiple objects falling inside the ROI. While most tracks with multiple objects within an ROI were sorted out during labeling, tracks where it was assessed that the object of interest was visible enough were still allowed. Figure 6 depicts such an example, where 2 cyclists are riding closely together. The system erroneously classifies this track as a car for most of its lifetime. The same happens in other tracks, where e.g. pedestrians are crossing the street in groups, or when a pedestrian is walking slowly near parked cars. This highlights an inherent weakness of the approach, namely that of overlapping targets, since the train set contains mainly frames where only one single target is present in the ROI.
4.1 Filtering the classifications
By applying a high level filter on top of the classifier, the classification performance could be improved, since tracks with small percentages of misclassified frames (the majority) would tend to 0 % misclassifications. Nonetheless, tracks with big percentages of misclassified frames will tend to even higher percentages, but since they are the minority, an overall improvement would be achieved.
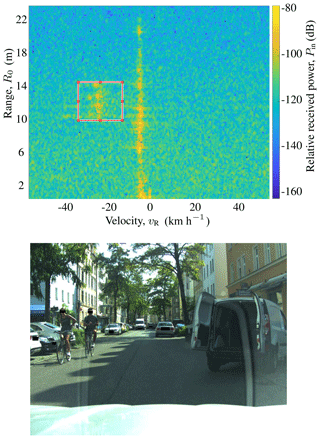
Figure 6Exemplary frame, where two bicycles fall within one single ROI, which leads to a high percentage of misclassified frames within the track. Photograph source: [Authors].
For this purpose a discrete Bayes filter (DBF) was chosen. An object is modeled as a random state variable X and the four classes (pedestrian, cyclist, car and noise) represent the discrete states xc that X can take on. The goal of a DBF is to recursively estimate at time t the discrete posterior probability distribution
where z1 : t stands for all measurements up to time t, by assigning a probability pc,t to each of the single states. The working principle of the DBF can be taken from Algorithm Discrete Bayes filter. Adapted from p. 87. Require: {pc,t-1},zt for all c do p‾c,t=∑ip(Xt=xc|Xt-1=xi)pi,t-1=pc,t-1 pc,t=ηp(zt|Xt=xc)p‾c,t end for return {pc,t} (Thrun et al., 2005). For a single object at time t the function loops over all four possible states (classes) xc and computes their respective probability pc,t. To do this, first the so called prediction, or prior, is calculated in line 2. The term is called the state transition probability and it represents the probability of going from state xi at time t−1 to state xc at time t. Here it is assumed that an object cannot change classes during its lifetime. Therefore, it follows that
and thus . In line 3 the current measurement zt is incorporated by multiplying its likelihood with the prior. The measurement zt at time t corresponds to the class with the highest probability as predicted by the CNN and its likelihood is derived from the statistics given by the confusion matrix in the top half of Table 4. Since the product is usually not a probability, a normalization factor η makes sure that the sum of all pc,t add up to one and thus, that {pc,t} is a probability distribution. When a new track is started, the DBF needs an initial probability distribution to compute the first estimate. Since no knowledge about the initial state is assumed, a uniform distribution is assigned to it.
Discrete Bayes filter. Adapted from Thrun et al. (2005, p. 87).
- Require:
1
2for all c do
3
4
5end for
6return {pc,t}
The results from applying the discrete Bayes filter can be taken from the bottom half of Table 4. The confusion matrix clearly shows an improvement of the classification accuracy for all classes. From the bottom half of Table 5 the precision and recall after applying the DBF can be seen. A substantial improvement of the recall for both pedestrian and cyclist classes is observed. A histogram of the relative number of errors per track after incorporating the DBF is also shown in Fig. 7. It can be seen that one clear drawback of this approach is that the number of completely misclassified tracks increases. These are the tracks that already had a high percentage of misclassified frames to begin with. Still, the overall classification accuracy improves from 0.84 to 0.91 after applying the DBF.
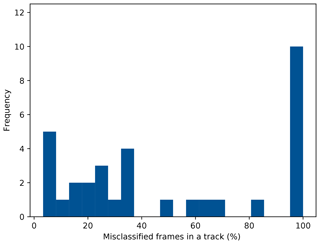
Figure 7Histogram of the relative number of erroneously classified frames per track after the discrete Bayes filter. Tracks without any misclassified frames are not included.
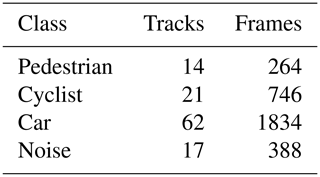
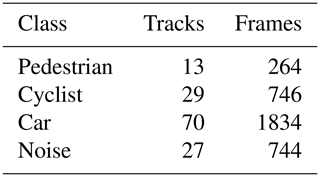
Since the likelihood values needed for the DBF were taken from the confusion matrix on Table 4, a new set of measurements is needed to make sure that the proposed filter doesn't only work with that specific dataset. A different set of data (see Table 6) was used to evaluate again the improvement after applying the DBF. The results for this set are laid out on Table 7. It is evident, that the filter improves the overall classification performance for this data set as well. In this case the overall accuracies are 0.91 before and 0.94 after the DBF.
This work presented a system to classify detected objects as either pedestrians, cyclists, cars or noise in urban automotive scenarios. It does so by first detecting the objects using a lidar sensor, extracting a region of interest from the radar range-Doppler-angle power spectrum and running it through a deep convolutional neural network. Training and test data sets were gathered using a test vehicle in real urban scenarios. The test results showed that the CNN reliably correctly classifies cars and empty ROIs (noise), but has trouble with the pedestrian and cyclist classes. Overlapping targets also present a big challenge for the system, since the network was trained mainly with ROIs which contain only one target. It was shown, that for many of the tracks only a small fraction of frames were misclassified, which could be improved by applying a tracking filter on top of the classifier. For this purpose a discrete Bayes filter was chosen, which significantly improved the classification performance for the pedestrian and cyclist classes. The improvements achieved with the DBF were validated using a new test data set.
Future work will focus on improving the classification performance by introducing the temporal information directly into the neural network, developing an approach to handle overlapping targets and increasing the number of classes.
The data used in this paper is available upon request.
RP developed the concept, gathered the data and evaluated the performance of the system. RP prepared the manuscript with feedback from FS, RR and EB. FS, RR and EB supervised the project and provided resources.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Kleinheubacher Berichte 2018”. It is a result of the Kleinheubacher Tagung 2018, Miltenberg, Germany, 24–26 September 2018.
This study was done in cooperation with BMW Group. Special thanks to BMW Group for supplying the test vehicle.
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
This paper was edited by Jens Anders and reviewed by two anonymous referees.
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G. S., Davis, A., Dean, J., Devin, M., Ghemawat, S., Goodfellow, I., Harp, A., Irving, G., Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kudlur, M., Levenberg, J., Mané, D., Monga, R., Moore, S., Murray, D., Olah, C., Schuster, M., Shlens, J., Steiner, B., Sutskever, I., Talwar, K., Tucker, P., Vanhoucke, V., Vasudevan, V., Viégas, F., Vinyals, O., Warden, P., Wattenberg, M., Wicke, M., Yu, Y., and Zheng, X.: TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, available at: https://www.tensorflow.org/ (last access: 13 August 2019), 2015. a
Chen, V. C., Li, F., Ho, S.-S., and Wechsler, H.: Micro-Doppler effect in radar: phenomenon, model, and simulation study, IEEE T. Aero. Elec. Sys., 42, 2–21, https://doi.org/10.1109/TAES.2006.1603402, 2006. a
European Commission: Traffic Safety Basic Facts on Cyclists, available at: https://ec.europa.eu/transport/road_safety/sites/roadsafety/files/pdf/statistics/dacota/bfs2017_cyclists.pdf (last access: 23 November 2018), 2017a. a
European Commission: Traffic Safety Basic Facts on Pedestrians, available at: https://ec.europa.eu/transport/road_safety/sites/roadsafety/files/pdf/statistics/dacota/bfs2017_pedestrians.pdf (last access: 23 November 2018), 2017b. a
Heuel, S. and Rohling, H.: Pedestrian classification in automotive radar systems, 13th International Radar Symposium, 39–44, IEEE, Piscataway, New Jersey, USA, https://doi.org/10.1109/IRS.2012.6233285, 2012. a
Jokanovic, B., Amin, M., and Ahmad, F.: Radar fall motion detection using deep learning, IEEE Radar Conference (RadarConf), 1–6, IEEE, Piscataway, New Jersey, USA, https://doi.org/10.1109/RADAR.2016.7485147, 2016. a
Mendis, G. J., Randeny, T., Wei, J., and Madanayake, A.: Deep learning based doppler radar for micro UAS detection and classification, MILCOM 2016 – 2016 IEEE Military Communications Conference, 924–929, IEEE, Piscataway, New Jersey, USA, https://doi.org/10.1109/MILCOM.2016.7795448, 2016. a
Prophet, R., Hoffmann, M., Vossiek, M., Sturm, C., Ossowska, A., Malik, W., and Lübbert, U.: Pedestrian Classification with a 79 GHz Automotive Radar Sensor, 19th International Radar Symposium (IRS), 1–6, IEEE, Piscataway, New Jersey, USA, https://doi.org/10.23919/IRS.2018.8448161, 2018. a
Pérez, R., Schubert, F., Rasshofer, R., and Biebl, E.: Single-Frame Vulnerable Road Users Classification with a 77 GHz FMCW Radar Sensor and a Convolutional Neural Network, 19th International Radar Symposium (IRS), 1–10, IEEE, Piscataway, New Jersey, USA, https://doi.org/10.23919/IRS.2018.8448126, 2018. a, b, c
Qi, C. R., Yi, L., Su, H., and Guibas, L. J.: PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space, CoRR, abs/1706.02413, http://arxiv.org/abs/1706.02413, 2017. a
Schumann, O., Hahn, M., Dickmann, J., and Wöhler, C.: Semantic Segmentation on Radar Point Clouds, 21st International Conference on Information Fusion (FUSION), 2179–2186, IEEE, Piscataway, New Jersey, USA, https://doi.org/10.23919/ICIF.2018.8455344, 2018. a
Shalev-Shwartz, S. and Ben-David, S.: Understanding Machine Learning: From Theory to Algorithms, Cambridge University Press, New York, New York, USA, https://doi.org/10.1017/CBO9781107298019, 2014. a
Simonyan, K. and Zisserman, A.: Very Deep Convolutional Networks for Large-Scale Image Recognition, CoRR, abs/1409.1556, http://arxiv.org/abs/1409.1556, 2014. a, b
Thrun, S., Burgard, W., Fox, D., and Arkin, R.: Probabilistic Robotics, Intelligent robotics and autonomous agents, MIT Press, Cambridge, Massachusetts, USA, 2005. a, b