A Low-Power Squaring Circuit with Regulated Output and Improved Settling Time in 180 nm CMOS for 3–5 GHz IR-UWB Applications
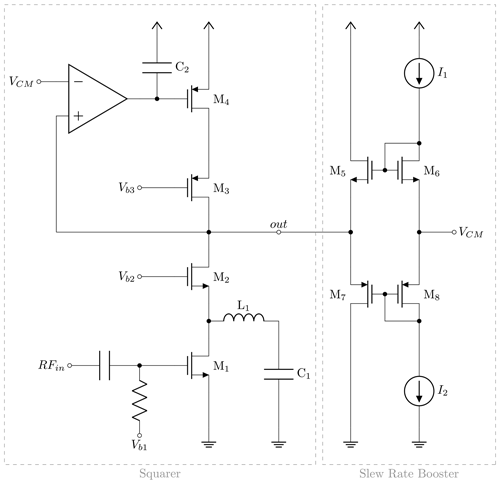
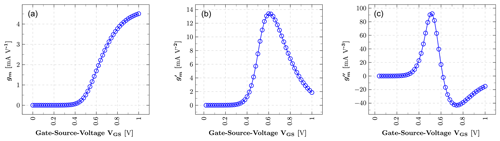
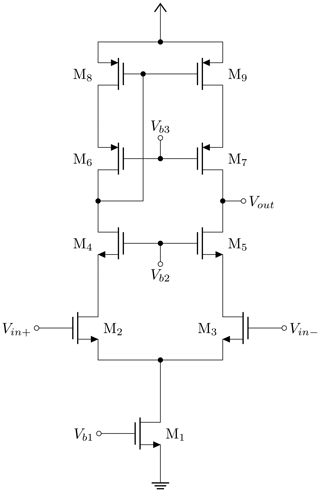
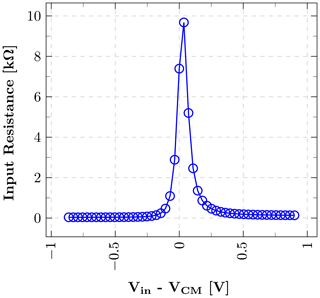
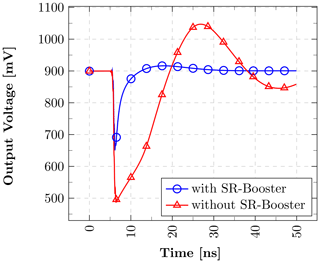
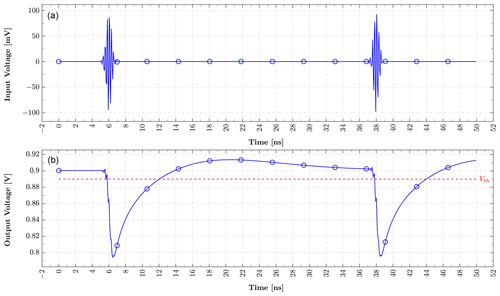
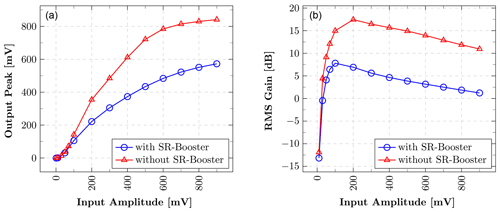
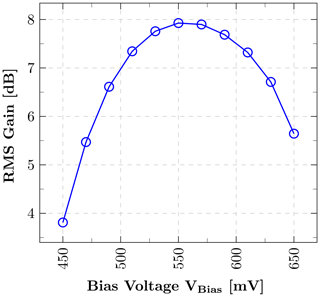
This paper demonstrates a low-power squaring circuit for 3–5 GHz non-coherent Impulse-Radio Ultra-Wideband (IR-UWB) receivers for Pulse Position Modulation (PPM) in a low-cost 180 nm CMOS technology. The squaring, which is the key element in typical IR-UWB receivers, is performed exploiting the non-linear transfer function of a MOS transistor. For a high gain at low power consumption the transistor is biased in the moderate inversion region, where the second-order derivative of the transconductance gm and, as a result, the quadratic term in the transfer function reaches a maximum. A control loop was implemented to set the dc output voltage to a defined value and thus to allow a comparison of the squarer output signal with a defined threshold voltage, which can easily be set and adjusted (e.g. by a DAC). To speed up the settling time of the output and hence to reach higher data rates, a novel slew-rate booster is implemented at the output. Thereby, the squarer is capable of data rates of up to 15.6 Mbit s−1, which is more than two times higher compared to the circuit without the slew-rate booster, while only consuming 72.4 µW in addition. In the extracted post-layout simulations the whole circuitry consumes 724 µA at a 1.8 V power supply, resulting in a power consumption of 1.3 mW.