Y-shaped tunable monolithic dual colour lasers for THz technology

THz generation by difference frequency generation can be accomplished by many different laser systems. The most cost efficient and compact solution will be monolithic dual-colour lasers. Application of these lasers in THz metrology can suffer from several drawbacks like coupling between the modes, strong amplitude variations, low tuning capabilities, or a complicated growth process. We discuss the impact of these points for THz measurements and present a simple monolithic dual colour laser which can be used for material characterisations.

1 Introduction

Photonic Terahertz (THz) technology is particularly attractive for non-destructive testing, as for example, thickness measurements (Krimi et al., 2016). Photonic THz systems split into two main groups: Time domain spectroscopy (TDS) and continuous wave (CW) THz systems. While TDs systems require scanning in the time domain, frequency scanning is performed in CW systems in order to receive sample-specific information. In contrast to TDS systems, a higher frequency resolution can be achieved with CW THz systems (Hübers et al., 2011). Currently, fast scanned CW systems outperform TDS systems in terms of speed and usability (Liebermeister et al., 2021). However, for practical industrial applications, such systems incorporating two separate lasers with variable difference frequency are still rather complex and expensive. Tunable dual colour (Matus et al., 2004), and in particular tunable monolithic dual colour lasers are a promising tool for simple and cost-efficient CW THz systems and are therefore analysed in this work with emphasis on their suitability for THz thickness measurements.

Tunable monolithic dual colour lasers often use a Y-shaped geometry with two independently tunable resonator branches. Wavelength control may be employed with distributed Bragg reflector (DBR) (Gwaro et al., 2020) or distributed feedback (DFB) (Surkamp et al., 2021) sections. Wavelength tuning of one or both sections can be realised by altering the refractive index by current induced heating or carrier density changes. An additional advantage of monolithic dual colour lasers for CW THz systems is the automatic spatial overlap of both modes which eliminates the demand for spatial mode-matching (Murasawa and Hidaka, 2010). Moreover, when using a common gain section for both optical modes, the correlation between the modes is increased which can result in lower noise of the difference frequency.

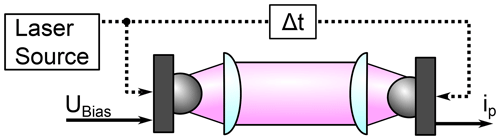
Such systems are typically implemented into a homodyne THz configuration like shown in Fig. 1 (Göbel et al., 2012; Moon et al., 2014). The dual colour output of the laser is split into two parts. The first part is sent to a THz transmitter (e.g. a THz photodiode or a photoconductive antenna (Sartorius et al., 2012; Preu et al., 2011)) that generates the difference frequency of the two colours in the THz range. This THz signal is passing the device under test and then reaches the THz receiver (e.g. also a photoconductive antenna). At this receiver the THz signal is mixed with a reference signal that stems from the second part of the split laser output which has passed through a reference arm that mostly contains a variable delay stage for sampling (Gwaro et al., 2020). Alternatively, sampling can be performed by frequency tuning (Moon et al., 2014; Surkamp et al., 2021).

For practical THz metrology applications tuning of the difference frequency of the two laser modes is preferred. The detailed tuning requirements should be considered in the design process as early as possible. Depending on the design, the capabilities of the devices are very different. Tuning capabilities can range from no tuning at all (Murasawa and Hidaka, 2010; Osborne et al., 2008) over a few selected difference frequencies between with a small mode-hop-free tuning range (Yang et al., 2015; Surkamp et al., 2021), up to a tuning range of 800 GHz in 1 GHz steps (Moon et al., 2014). For Fabry Pérot type lasers, the tuning might be restricted to a frequency grid based on the cavity round trip frequency (Gwaro et al., 2020). Tuning itself is either done by temperature (Moon et al., 2014; Gwaro et al., 2020), current (Carpintero et al., 2014) or a combination of both (Yang et al., 2015; Surkamp et al., 2021).

The THz metrology applications based on two-colour lasers may suffer from imperfections of the lasers like limited tuning range, discontinuous tuning, amplitude differences (Göbel et al., 2012) due to mode competition or cross-talk between the modes (Carpintero et al., 2014).

In the following we will discuss the impact of imperfections in the dual colour emission process based on a simple numerical analysis and by comparing the performance of two different device designs, to suggest a laser system usable for cost effective straightforward THz thickness measurements.

Figure 1 Basic THz measurement setup. The dual-colour laser source is split into two arms. In one arm a delay stage can be used to introduce a variable time delay Δ t.

2 THz traces

For most THz measurements it is crucial to identify amplitude and phase of the THz wave. The most straightforward approach is a scan in time domain (TD) with a delay stage like shown in Fig. 1. But this approach is not favourable if a high measurement speed is necessary. However, equivalent information can be extracted in the frequency domain (FD) (Mouret et al., 2007) by frequency tuning. This tuning can be very fast, when using current tuning while being comparable to delay stage speeds when using temperature tuning. For application with large frequency tuning requirements, current tuning might not be suitable, though.

The detected photocurrent (i_p) is based on the mixing process and can be estimated by the following equation (Mouret et al., 2007):

$$\begin{array}{}\text{(1)}& {\mathrm{i}}_{\mathrm{p}}\left(\mathrm{\Delta }\mathit{\omega },\mathrm{\Delta }L\right)\propto {\mathrm{E}}_{\mathrm{THz}}\cos \left(\mathrm{\Delta }\mathit{\omega }\mathrm{\Delta }L/c+\mathrm{\Delta }\mathit{\varphi }\right),\end{array}$$

where E_THz is the amplitude of the THz field, Δω the difference frequency, ΔL the path length difference between transmitter and receiver arm, c the speed of light, and Δϕ the phase offset of the system. Furthermore we assume

$$\begin{array}{}\text{(2)}& E_{\mathrm{THz}}\propto {\sum }_{i=\mathrm{1}}^{n-\mathrm{1}}{\sum }_{j=i}^n{\mathrm{E}}_i\times E_j,\end{array}$$

where n is the total number of modes. More detailed simulations for multimode emission of diode lasers can be found in (Scheller et al., 2009) and (Kolpatzeck et al., 2020). The default signal based on a scan in TD and FD is shown in Fig. 2a. For the extraction of amplitude and phase of the THz signal, it is mandatory to complete a scan which contains at least half a period in either of the two directions (TD or FD). In terms of speed, a scan in FD is the preferred scanning mechanism. With increasing ΔL, the necessary tuning range Δω can be reduced, while the modulation in FD disappears at ΔL=0.

Consequently, we can adapt the system to the tuning capabilities of the available laser by choosing the correct ΔL to scan a full period of the interference term. Small tuning can be sufficient for large ΔL, while the impact of the sample can be very small in this case (Mouret et al., 2007). Large tuning allows for small ΔL, but needs a laser system which is capable of covering a large tuning range (Moon et al., 2014), with a probable reduction in scanning speed.

Before practical use, the consequences of imperfect dual colour tuning have to be considered. Consequently, the impact of mode competition, multi-mode emission, and frequency grids due to residual Fabry-Pérot modes must be considered as they can have significant detrimental effects on the THz signal, especially for scans in FD. In the following, we will discuss separately the different impacts of these effects, before showing an example how these effects may interact to corrupt the tuning behaviour of a two colour laser.

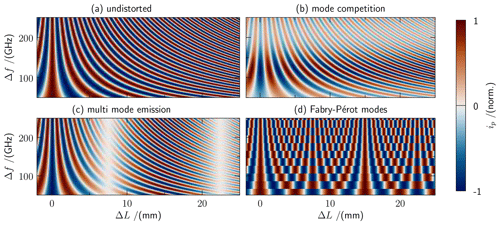
Figure 2 Simulated photocurrent i_p at the THz receiver for different effects. (a) undistorted signal for varying delay length ΔL and difference frequency Δf. (b) mode competition: amplitude ratio between the two modes changes with changing difference frequency. Identical amplitudes for both modes at 120 GHz. (c) multi-mode emission: one mode is split into two with a frequency distance of 20 GHz. This results in a beating of the THz signal with a period of 15 mm for a delay line scan. (d) Fabry-Pérot modes: difference frequency dominated by Fabry-Pérot modes of the monolithic cavity. Only fixed difference frequencies are available and the signal repeats in TD based on the cavity roundtrip time.

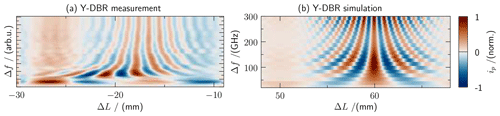
Figure 3 (a) Y-DBR measurement: THz signal for DBR laser (normalized) in dependence of heater current (Δf) and path length difference (ΔL). (b) Y-DBR simulation: THz signal including all effects as discussed in Fig. 2. Difference in ΔL is given by zero position of delay stage.

Current tuning as well as temperature tuning might result in a change of the amplitude ratios of the two optical modes, even though the overall optical power stays constant. This will reduce the efficiency of the mixing process in the emitter and consequently E_THz as well as i_p will be decreased. A common gain section in a monolithic device will have a similar effect as one of the two modes will typically be favourable. The amplitude ratio of the optical modes is usually based on the operational settings of the dual colour laser, which allows for sufficient stability over time to perform a scan in TD (see Fig. 2b). A scan in FD is more challenging but can be accomplished by using a look-up table as a reference if the behaviour of the laser is deterministic and the tuning capabilities of the lasers are sufficient. However, depending on the laser design, only fixed difference frequencies might be possible (Yang et al., 2015).

If one (or both) of the two colours consist of multiple frequencies, all possible difference frequencies will be emitted at the transmitter. The simulation for three optical modes (f₁≈193.5THz, $f_{\mathrm{2}}=f_{\mathrm{1}}+\mathrm{20}$ GHz $f_{\mathrm{3}}=f_{\mathrm{1}}+\mathrm{\Delta }f)$ is shown in Fig. 2c. Due to the superposition of all difference frequencies in the THz range, the THz signal will be strongly decreased for some ranges of ΔL. A scan in TD will show the corresponding beating of all difference frequencies. A scan in FD might be impossible or strongly affected by the number and amplitude of the emitted optical modes. Like before, a look-up table might be necessary to perform any kind of THz measurements. For a multimode laser, the output can result in a quasi-pulse like THz trace, where the THz signal is only visible if ΔL matches integer multiples of the cavity roundtrip frequency of the laser (Brenner et al., 2018; Morikawa et al., 1999).

A fixed frequency grid due to Fabry-Pérot modes of a monolithic laser might result in the biggest problems, as it can dominate the correlation between Δω and ΔL, resulting in a highly reduced parameter space. A shared gain section in the device can result in an additional coupling of the emission frequencies which results in a very strong effect. If both modes are integer multiples of the same fundamental frequency, the THz trace will show a repetitive behaviour like shown in Fig. 2d. If the tuning is limited to these frequency steps, the THz signal will repeat itself with a period which corresponds to the cavity length. A scan in TD can be performed like usual with a limited range, but a scan in FD might be impossible.

Figure 4 Optical spectrum of the slotted Y-branch dual mode laser.

Next, we analyse the tuning behaviour of a Y-branch two colour DBR laser that had been developed for Raman spectroscopy (Gwaro et al., 2020). The laser is grown by metalorganic vapour-phase epitaxy and emits at two wavelength simultaneously at 785 nm with a tunable difference frequency of 180–316 GHz. Tuning is accomplished with a resistor heater for one arm of the Y-shaped cavity. The length of the device is 3 mm which corresponds to a free spectral range of the cavity modes of approximately 15 GHz.

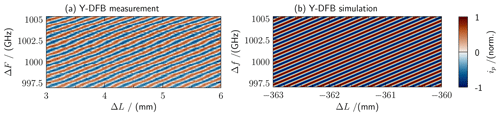
Figure 5 (a) Measured THz signal for DFB laser (normalized) in dependence of difference frequency (Δf) and path length difference (ΔL). (b) Simulated THz signal.

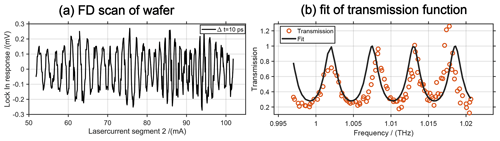
Figure 6 (a) FD scan of wafer: THz transmission data of HRFZ silicon wafer at constant time delay of Δt = 10 ps. (b) fit of the transmission function: Red circles show measured transmission, while black line shows fit.

Figure 3a shows a measured colour map of the THz signal as a function of heater current (for temperature tuning) and delay position. Obviously, the behaviour differs strongly from the ideal tuning behaviour as shown in Fig. 2a. Unfortunately, no region can be found in which temperature tuning could unambiguously provide amplitude and phase of the THz signal. In order to determine the dominant effects hindering a clean tuning behaviour, we numerically qualitatively reproduced the experimentally observed behaviour by superimposing the detrimental effects discussed above and shown in Fig. 2b–d. The result is shown in Fig. 3b. We achieve this good qualitative agreement with experiment by considering multimode emission (each of the two main modes is split into three modes) and a frequency grid spacing of 15 GHz due to residual Fabry Perot modes. Effects of mode competition were of minor importance. Thus, the residual frequency grid prevents continuous tunability, and multimode emission additionally limits the tuning range. Accordingly, for two colour lasers for THz metrology applications, great care has to be taken to suppress Fabry-Pérot effects when DBR or DFB spectral control is employed and to achieve pure two colour emission with one mode per colour only. Obviously, amplitude differences of the two modes are less detrimental.

In the next section, we investigate a different laser scheme providing a smaller overall tuning range but continuous pure two colour tunability and show that is suitable for the envisioned THz metrology application.

3 Current tuned slotted Y-branch laser at 1550 nm

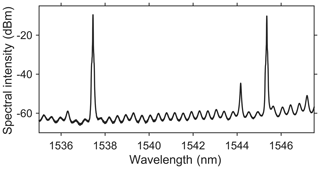
The dual colour laser for the following experiments is based on an InP/AlGaInAs/GaInAs material system that provides gain in the 1550 nm region. The laser waveguide has a Y-branch included and consists of three electrically isolated segments: one common gain segment and the two arms. The arms include an etched grating of high order, often referred to as slots, which provide the spectrally selective feedback mechanism (Surkamp et al., 2021). As it can be seen in Fig. 4, the spectral feedback is designed such that a dual mode emission with a difference frequency in the range of 1 THz is generated. By changing the point of operation by a variation of the applied current, a continuous shift of the spectrum can be obtained due to current induced changes of the refractive index. When tuning the current on a single segment, a tuning of ± 10.5 GHz around the design difference frequency of 1 THz can be obtained. Moreover, a second regime of operation is available with a difference frequency of 0.85 THz and a tuning range of ±6.5 GHz. Here the third mode that can be observed at around 1544 nm in Fig. 4 becomes dominant over the long wavelength mode.

Figure 5a shows a colour map of the THz signal as a function of frequency tuning and delay. Obviously, the tuning range is limited but clean continuous tuning is obtained as reproduced in the simulation shown in Fig. 5b. Thus, we expect this laser to be suitable for THz thickness measurements and show a proof of concept in the following. By tuning the current applied to one of both arms the emitted difference frequency in the THz range is continuously tuned over a small frequency region and a THz trace can be measured without any movement of the optical delay stage. However, this tuning can be sufficient to extract the relevant information from a sample. An example of such a measurement for material characterization is presented in Fig. 6a. Here a high resistive float zone (HRFZ) silicon wafer of 8 mm geometrical thickness is placed in the terahertz transmission path. The trace shows two oscillations: a fast one originating in the measurement at a path length difference ΔL≠0 and a slowly varying envelope that is attributed to the sample induced etalon effect.

For material analysis, only the envelopes of reference and sample measurement have to be considered. This could be done by peak detection (of the fastly varying fringes) or using the Hilbert transformation. Dividing the absolute square of sample measurement and reference measurement results in the sample transmission (red circles in Fig. 6b) which is subsequently used for MSE fit of the theoretical etalon transmission. Figure 6b shows the processed data from Fig. 6a together with a fit of the theoretical etalon transmission. Transmission values larger than 1 can be observed due to noise present in sample and reference measurement. The sample thickness d and refractive index n of the wafer samples are determined as described in Surkamp et al. (2021). For the sample with a nominal thickness of 8 mm and refractive index of 3.417 (Dai et al., 2004), the lowest mean square error results in $d=\mathrm{7},\mathrm{75}$ mm and $n=\mathrm{3},\mathrm{494}$, which corresponds to an error of less than 5 %.

4 Summary and conclusion

Monolithic dual mode lasers can be a valuable tool for continuous wave THz measurements. Although large tuning ranges of the difference frequency allow for more flexible approaches, small tuning ranges can be sufficient for certain applications. Based on the design choices of the device several problems like amplitude variance, multi-mode emission, and discrete tuning steps can occur. We showed the impact of these distortions and presented a system which is capable of material parameter extraction with the potential for high-speed measurements.