Uncertainties of S-Parameter Measurements in Rectangular Waveguides at PTB

In this work the determination of measurement uncertainties in scattering parameter measurements for waveguide interfaces ranging from R 100 (WR 90) to R 2.6k (WR 3, WM-864) is presented. For each waveguide band a Thru Reflect Line calibration is performed including uncertainties for calibration standards, cable movement, interface repeatability and the characteristics of the vector network analyzer. For reflection and transmission coefficients, envelopes of uncertainties are determined for magnitude and phase angle respectively. In addition, an experiment on connection (interface) repeatability for R 140 was carried out to systematically investigate the influence of shifting and rotating of waveguide flanges. Translation values in steps of 0.3 mm up to 1.5 mm are examined in simulation as well as measurement. The findings of these investigations can be extended and applied to other waveguide bands.

1 Introduction

National metrology institutes (NMIs) like the Physikalisch-Technische Bundesanstalt (PTB) usually are the highest authority in metrology in the corresponding country. Each NMI submits its calibration and measurement capabilities (CMCs) to the Bureau International des Poids et Mesures (BIPM) providing a quantitative assessment of the NMI's precision and accuracy for specific measurements. Approval only follows after a successful review from experts from the regional metrology organization (RMO), e.g. EURAMET in Europe, as well as one inter RMO review. PTB's current CMCs of scattering parameters (S-parameters) for waveguide measurements were approved 24 July 2023 (BIPM, 2024). The corresponding institute service codes as well as CMC IDs in brackets are:

• 2.2.541 (EURAMET-EM-DE-00000FAR-5) for reflection magnitude,

• 2.2.541b (EURAMET-EM-DE-00000OY3-1) for reflection phase angle,

• 2.2.542a (EURAMET-EM-DE-00000OY2-1) for transmission magnitude and

• 2.2.542b (EURAMET-EM-DE-00000OY0-1) for transmission phase angle.

Each underlying uncertainty matrix covers steps in nominal magnitude (0–1 for reflection and −80–0 dB for transmission) for waveguide interfaces ranging from R 100 (WR 90, 8.2 to 12.5 GHz) to R 1.8k (WR 5, WM-1295, 140 to 200 GHz) as standardized by IEC (2016). Section 2 of this work covers the methodology with which the CMC values were achieved. Additionally, the calculations described are extended to the R 2.6k (WR 3, WM-864) band. The results are presented in Sect. 3 for each of the four measurands listed above. Main uncertainty influences are discussed and investigated further in Sect. 4, in which the experiment on connection (interface) repeatability is carried out. Part of this section was also presented during the Kleinheubacher Tagung 2017.

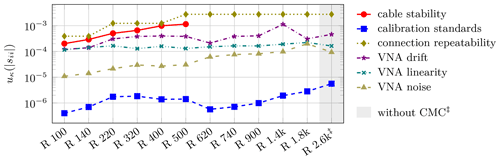
Figure 1 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide reflection magnitude measurements with nominal magnitude $\left|s_{ii}\right|=\mathrm{0.2}$ for waveguides ranging from R 100 (WR 90) to R 2.6k (WR 3, WM-864).

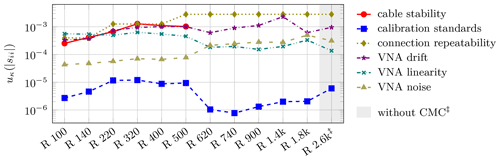
Figure 2 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide reflection magnitude measurements with nominal magnitude $\left|s_{ii}\right|=\mathrm{1.0}$ for waveguides ranging from R 100 (WR 90) to R 2.6k (WR 3, WM-864).

Table 1 Calibration and measurement capabilities of waveguide reflection coefficient magnitude $U\left(\right|s_{ii}\left|\right)$ with k=2, taken from KCDB 2.2.541 and expanded with R 2.6k (WR 3).

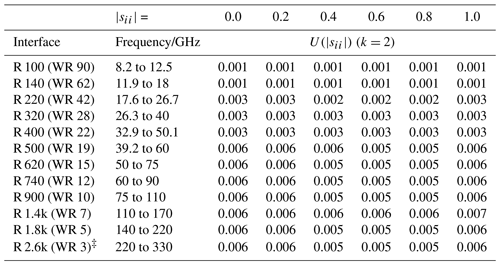
Values for R 2.6k (WR 3) marked by ^‡ have not yet been submitted and accepted as CMC yet.

Table 2 Calibration and measurement capabilities of waveguide reflection coefficient phase angle $U\left(\right|s_{ii}\left|\right)$ with k=2 taken from KCDB 2.2.541b and expanded with R 2.6k (WR 3).

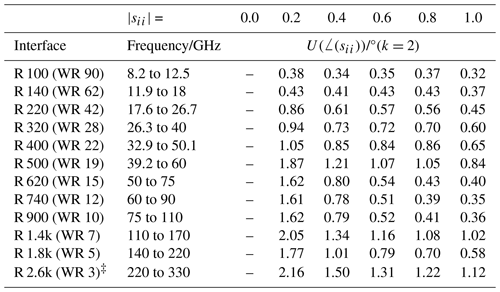
Values for R 2.6k (WR 3) marked by ^‡ have not yet been submitted and accepted.

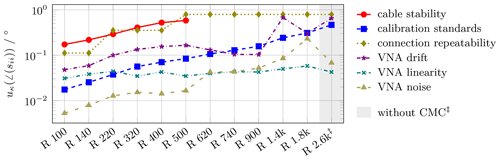
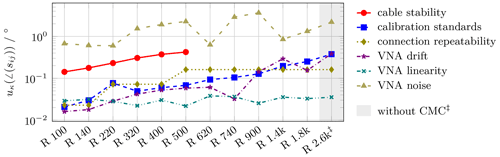
Figure 3 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide reflection phase angle measurements with nominal magnitude $\left|s_{ii}\right|=\mathrm{0.2}$ for waveguides ranging from R 100 (WR 90) down in size to R 2.6k (WR 3, WM-864).

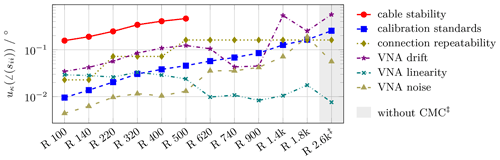
Figure 4 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide reflection phase angle measurements with nominal magnitude $\left|s_{ii}\right|=\mathrm{1.0}$ for waveguides ranging from R 100 (WR 90) down in size to R 2.6k (WR 3, WM-864).

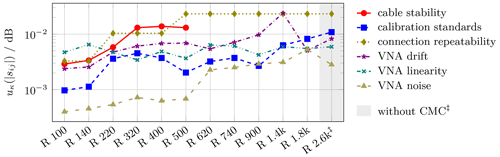
Figure 5 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide transmission magnitude measurements with nominal magnitude $\left|s_{ij}\right|$ = -10 dB for waveguides ranging from R 100 (WR 90) down in size to R 2.6k (WR 3, WM-864).

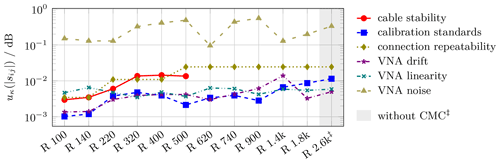
Figure 6 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide transmission magnitude measurements with nominal magnitude $\left|s_{ij}\right|$ = -80 dB for waveguides ranging from R 100 (WR 90) down in size to R 2.6k (WR 3, WM-864).

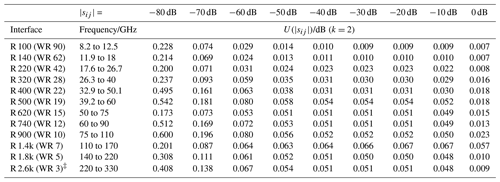
Table 3 Calibration and measurement capabilities of waveguide transmission coefficient magnitude $U\left(\right|s_{ij}\left|\right)$ with k=2 taken from KCDB 2.2.542a and expanded with R 2.6k (WR 3).

Values for R 2.6k (WR 3) marked by ^‡ have not yet been submitted and accepted.

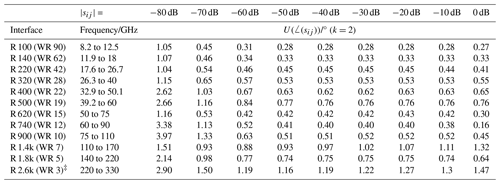
Table 4 Calibration and measurement capabilities of waveguide transmission coefficient phase angle U($\left|s_{ii}\right|)$ with k=2 taken from KCDB 2.2.542b and expanded with R 2.6k (WR 3).

Values for R 2.6k (WR 3) marked by ^‡ have not yet been submitted and accepted.

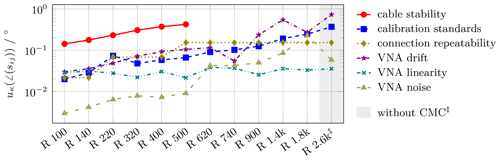
Figure 7 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide transmission magnitude measurements with nominal magnitude $\left|s_{ij}\right|$ = -10 dB for waveguides ranging from R 100 (WR 90) down in size to R 2.6k (WR 3, WM-864).

Figure 8 Uncertainty components c_κ⋅u_κ of the six main uncertainty contributions to waveguide transmission magnitude measurements with nominal magnitude $\left|s_{ij}\right|$ = −80 dB for waveguides ranging from R 100 (WR 90) down in size to R 2.6k (WR 3, WM-864).

2 Calculation Methodology

For each waveguide band, an artificial Thru Reflect Line (TRL) calibration following the methodology outlined in Engen and Hoer (1979) is conducted for symmetrical two-port devices, considering varying reflection and transmission coefficients. The magnitude of the reflection (s₁₁=s₂₂) is incrementally swept from 0 to 1 in steps of 0.2. Similarly, for transmission (s₁₂=s₂₁) the magnitude ranged from −80 to 0 dB in steps of 10 dB. These simulations were performed using MATLAB from Mathworks (2023) in conjunction with the METAS UncLib (Zeier et al., 2012). The ensuing statements align with the principles outlined in the EURAMET Calibration Guide No. 12 (CG-12) (Zeier et al., 2018) and pertain to each waveguide band under investigation.

For the bands R 100 to R 500, a standalone vector network analyzer (VNA) is utilized, while VNA extenders are employed for the bands R 620 to The generated Devices Under Test (DUTs) are cascaded with actual measured error boxes to simulate measurement data. Subsequently, the characteristics and associated uncertainties of VNA setups for each band are applied in accordance with METAS VNA Tools Math Reference (Wollensack and Hoffmann, 2023). Detailed discussions on these VNA influences are provided in Sect. 3. To accurately propagate uncertainties through the TRL algorithm, a recursive approach outlined by Stumper (2005) and Hall (2018) is employed. The resulting error boxes are then utilized to de-cascade the artificial DUT data. For each nominal magnitude in reflection or transmission, an envelope describing the maximum uncertainty in each waveguide's frequency range is determined for both magnitude and phase angle. These envelopes represent the minimum achievable uncertainty and are therefore reported as CMCs.

To comprehensively evaluate the impact of individual factors on the overall uncertainty, the METAS UncLib facilitates a detailed breakdown of the uncertainty budget. Key contributors to uncertainty include VNA noise, VNA linearity, VNA drift, connection repeatability, calibration standards and cable stability. Rigorous characterization of the VNA set-ups ensures that actual parameters are utilized for simulation purposes. Furthermore, repeatability is systematically assessed, although for practical reasons, an envelope approach is adopted to provide a conservative estimate. During calibration procedures, measured repeatability values take precedence, particularly if they surpass the envelope estimate, ensuring robust and precise calibrations. Cable stability considerations are limited to measurements conducted with the VNA base unit due to negligible movement paths, when using extenders and estimations in the R 900 band. However, for frequency-converting measurements, the impact of cable movement warrants further investigation, as highlighted by Novotny (2019), Arsenovic (2020) and Gellersen et al. (2024). Separate consideration of the cables for the local oscillator (LO) and other cables carrying the intermediate frequency (IF) and radio frequency (RF) signals are of interest. As these other cables operate at lower frequencies than the LO, their influence is assumed to be smaller.

For each influencing parameter κ the uncertainty contribution u_κ(s_ij) is defined as the product of sensitivity coefficient c_κ and standard uncertainty of that parameter u(κ) according to the Guide to the Expression of Uncertainty in Measurement (GUM, Working Group 1 of the Joint Committee for Guides in Metrology, 2008). The resulting standard uncertainty with k=1 of the measurement is calculated as the euclidean norm

$$\begin{array}{}\text{(1)}& u\left(s_{ij}\right)=\parallel u_{\mathit{\kappa }}\left(s_{ij}\right){\parallel }_{\mathrm{2}}=\parallel c_{\mathit{\kappa }}\cdot u\left(\mathit{\kappa }\right){\parallel }_{\mathrm{2}}=\sqrt{\sum _{\mathit{\kappa }}{\left(c_{\mathit{\kappa }}\cdot u\left(\mathit{\kappa }\right)\right)}^{\mathrm{2}}}.\end{array}$$

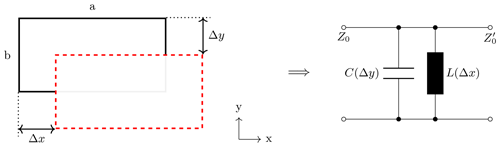
Figure 9 Misalignment of two waveguides of same size a by b represented as solid black and dashed red boxes on the left. Horizontal and vertical translations – Δx and Δy respectively – are varied between 0.0 and 1.5 mm. Misalignment causes parasitic capacitance C and inductance L (Marcuvitz, 1986) as shown on the right.

Figure 10 Precision flange adapters used to vary the misalignment of two waveguide interfaces. Steps of 0.3 mm are achieved in horizontal and vertical direction by choosing corresponding alignment holes on the left and right side of the waveguide interface. In this case, the alignment pin was inserted in the fifth row and fifth column, resulting in a misalignment of $\mathrm{\Delta }x=\mathrm{\Delta }y=$ 1.2 mm in both x- and y-directions.

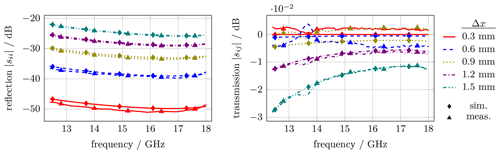
Figure 11 Simulation (sim.) and measurement (meas.) results for reflection and transmission coefficients for translation along the x axis (long WG side) ranging from 0.3 to 1.5 mm. Translation values are indicated by color and line style whereas simulation and measurement data are represented by different marker styles.

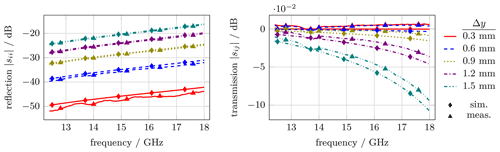
Figure 12 Simulation (sim.) and measurement (meas.) results for reflection and transmission coefficients for translation along the y axis (short WG side) ranging from 0.3 to 1.5 mm. Translation values are indicated by color and line style whereas simulation and measurement data are represented by different marker styles.

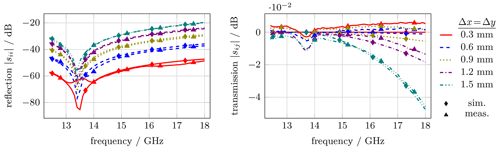
Figure 13 Simulation (sim.) and measurement (meas.) results for reflection and transmission coefficients for translation along the x axis (long WG side) and y axis (short WG side) ranging from 0.3 to 1.5 mm. Translation values are indicated by color and line style whereas simulation and measurement data are represented by different marker styles.

3 Calibration and Measurement Capabilities

The calculation of the CMCs of PTB covers the eleven waveguide bands ranging from R 100 to R 1.8k as approved in 2023. Additionally, the R 2.6k band - marked with ‡ and highlighted in gray in Figs. 1–8 – is also presented here. The expanded uncertainties (k=2) for magnitude and phase angle are summarized for different reflection and transmission values. In the reflection case, a high reflect DUT with $\left|s_{ii}\right|=\mathrm{1}$ and a low reflect DUT with $\left|s_{ii}\right|=\mathrm{0.2}$ are discussed. In the case of no reflection ($\left|s_{ii}\right|=\mathrm{0.0}$), the phase angle cannot be determined because the magnitude of the reflected wave tends towards zero. As for transmission, DUTs with $\left|s_{ij}\right|=-\mathrm{10}\text{dB}$ and $\left|s_{ij}\right|=-\mathrm{80}\text{dB}$ are investigated. To improve readability, only the arithmetic mean $\stackrel{\mathrm{‾}}{\left|c_{\mathit{\kappa }}\right|\cdot u\left(\mathit{\kappa }\right)}$ of the six main uncertainty contributions κ per waveguide band is shown. The notation $\stackrel{\mathrm{‾}}{\left(\mathrm{\dots }\right)}$ for the mean value is omitted for brevity in the following discussions.

3.1 Reflection Magnitude

Most waveguide DUTs that are calibrated at PTB are one-port devices (reflection only). Table 1 displays the current calculated an approved CMC values. Additionally, the waveguide size R 2.6k is included. The expanded uncertainty of the reflection magnitude $U\left(\right|s_{ii}\left|\right)$ ranges from 0.001 at R 100 to 0.006 at R 1.8k. In general, it rises as the waveguide decreases in size, while staying relatively stable despite variations in nominal reflection. The computation of R 2.6k adheres to this pattern, aligning consistently with previously validated CMCs. Figures 1 and 2 provide a simplified summary of the six uncertainty contributions $\stackrel{\mathrm{‾}}{\left|c_{\mathit{\kappa }}\right|\cdot u\left(\mathit{\kappa }\right)}$ to the reflection magnitude.

Figure 1 illustrates scenarios where the DUT induces minimal reflection, such as matches or loads. The primary source of uncertainty stems from the connection (interface) repeatability of the flange, encompassing translation in both E- and H-Plane, as well as interface rotation. Additionally, significant influences include cable stability, if applicable, and VNA drift for the measurement duration. The last factor must be considered due to the need for repeated connections of each DUT to evaluate the actual repeatability, necessitating a significant time investment. Typical VNA settings (number of measurement points, filter bandwidth, etc.) often results in frequency sweeping times of one minute or more for each used test port.

If a high reflect DUT like short terminations are calibrated, Fig. 2 shows that connection repeatability is still the main uncertainty influence. But cable stability, VNA drift as well as VNA linearity increase in importance. At higher frequencies VNA noise becomes also increasingly important. The general trend of reflection magnitude emphasizes that the calibration standards used always have the lowest influence. It is smaller by a factor of 10–100. This is probably due to correlation of the calibration standards used when renormalization is performed.

3.2 Reflection Phase Angle

In addition to the discussion on reflection magnitude, Table 2 provides a summary of the corresponding expanded phase angle uncertainties (k=2). Notably, the expanded uncertainties of the reflection phase angle U(∠(s_ii)) are presented in degrees for historical reasons. They range from 0.32° for R 100 to 2.05° for R 1.4k. Generally, the reported CMC values exhibit an increase for lower nominal reflection magnitude and smaller waveguides. The calculation for R 2.6k follows this trend, showing consistency with previously approved CMCs. Furthermore, Figs. 3 and 4 provide a simplified overview of the six uncertainty contributions $\stackrel{\mathrm{‾}}{\left|c_{\mathit{\kappa }}\right|\cdot u\left(\mathit{\kappa }\right)}$ to the reflection phase angle uncertainty.

For low loss DUTs like loads or matches depicted in Fig. 3 the main uncertainty contribution stems from the connection repeatability and cable stability, if considered. In contrast to the reflection magnitude in Fig. 1, the influence of calibration standards used on the reflection phase angle uncertainty increases significantly with smaller waveguide size. Similarly, the VNA noise influence increases. The R 1.4 and R 2.6k bands stand out due to the unusually high impact of VNA noise. These observations are mainly influenced by the performance of the used extender modules. VNA linearity has a comparatively small influence.

In contrast, Fig. 4 illustrates scenarios with high reflection magnitudes, such as short terminations. Notably, in bands R 100 to R 500, where cable stability is considered and no frequency extender is used, it emerges as the primary uncertainty influence. This underscores the necessity for further investigation, as highlighted by Novotny (2019), Arsenovic (2020) and Gellersen et al. (2024). The influence of calibration standards used and VNA drift becomes more pronounced for smaller waveguide sizes, while repeatability loses some significance. Please not, the repeatability is assumed to be −48 dB from R 620 to R 2.6k. This is very often an overestimation for the lower frequencies, while for 140 to 330 GHz the manufacturing of the DUT flanges must be excellent to achieve these values. The overall trend in reflection phase angle uncertainty underlines the growing significance of cable stability for highly reflective DUTs, along with the increasing importance of the calibration standards utilized during the calibration process. Consequently, it is reasonable to look into their sub-influences, such as material and dimensional parameters, akin to the approach adopted for coaxial offset shorts (Schramm et al., 2023). The influence of VNA drift follows a comparable pattern, albeit to a lesser extent.

3.3 Transmission Magnitude

Only a limited number of two-port DUTs, primarily consisting of shims and sometimes attenuators, undergo periodical calibration at PTB. Table 3 presents the minimum achievable expanded uncertainty on transmission magnitude $U\left(\right|s_{ii}\left|\right)$ (k=2). These CMC values vary from 0.007 dB for low transmission loss DUTs to 0.542 dB for high transmission loss DUTs. Notably, the uncertainty is heavily dependent upon the nominal transmission coefficient. Calculations for R 2.6k, though not yet part of CMC, align closely in scope. Figures 5 and 6 provide a simplified overview of the six uncertainty contributions $\stackrel{\mathrm{‾}}{\left|c_{\mathit{\kappa }}\right|\cdot u\left(\mathit{\kappa }\right)}$ to the transmission magnitude.

For low-loss DUTs, Fig. 5 shows the primary uncertainty components. Here, the principal influences correspond to those observed in the case of reflection magnitude, namely connection repeatability and cable stability. However, a notable difference lies in the non-negligible impact of calibration standards. Additionally, for smaller waveguide sizes, the influence of VNA noise rises by a factor of approximately 10. The peak in VNA drift contribution is attributed to the behavior of the VNA extender.

As apparent from Table 3 the expanded uncertainty for highly attenuated transmission e.g. $\left|s_{ij}\right|=-\mathrm{80}\mathrm{dB}$ notably increases. This becomes even more pronounced when examining the individual uncertainty components in Fig. 6. The uncertainty budget is primarily governed by the contribution of VNA noise, which is reasonable given that the nominal transmission value approaches the noise floor of the VNA setup utilized. Consequently, the significance of other influences diminishes.

3.4 Transmission Phase Angle

Analogous to the reflection case, Table 4 extends the transmission measurement to include the phase angle. The expanded uncertainties U(∠(s_ij)) with k=2 are expressed in degrees. The minimal phase uncertainty is achieved at 0.27° for a low loss waveguide of size R 100, while the maximum phase uncertainty is recorded at 3.97° for a high transmission loss waveguide of size R 900. Additionally, calculations for R 2.6k were conducted but are not yet part of the CMC. Figures 7 and 8 provide an overview over the six main uncertainty contributions $\stackrel{\mathrm{‾}}{\left|c_{\mathit{\kappa }}\right|\cdot u\left(\mathit{\kappa }\right)}$.

Contrary to the reflection phase angle, the transmission phase angle uncertainty for low loss DUTs is mainly determined by cable stability, VNA drift and the calibration standards. Once again, the great importance of the connection repeatability as well as the calibration standards used should be emphasized. Analogous to the behavior shown in Schramm et al. (2023), it can be assumed for waveguide measurements that the material parameters will have a major influence. For DUTs with higher transmission losses, a similar behavior to the reflection phase angle is observed: the predominant uncertainty component arises from VNA noise, as the transmitted wave approaches the noise floor of the VNA. All other five influences exhibit a similar behavior to the low-loss DUT.

4 Scaled Measurements

As seen in Sect. 3 the repeatability of the connection interface is a major uncertainty contribution to the magnitude as well as phase of the reflection and transmission coefficients. It should also be noted that the observations are a conservative envelope curve that represents the expected normal case.

While the repeatability for standardized flanges is usually predictable to a certain precision, one should always perform measurement series to verify such numbers. Without measurements the interpretation of the standardized mechanical definitions (and tolerance) in regard to the electrical performance (namely repeatability) is usually done by numerical simulation with CST Microwave Studio, HFSS, COMSOL Multiphysics or other comparable tools. The simulation results yield better results for displacement and rotation than approximations or analytical model like Hunter (1984). But even with modern software and powerful computing hardware, it can still be laborious to reach more than three significant digits of precision. In order to estimate the magnitude of the effect of displacements and rotations at the contact point of two waveguides, scaled measurement were performed, while first results were reported during the Kleinheubacher Tagung 2017. To do the actual measurements, special port adapters are needed, which are discussed briefly in Sect. 4.1. The measurements for reflection and transmission are compared with simulations carried out in CST Microwave Studio (Dassault Systèmes, 2024) and the results are summarized in Sect. 4.2.

4.1 Measurement Setup and Method

The actual connection repeatability is different for each flange, a function of the frequency, and can e.g. be determined by measurement series. Due to the principle of scaled measurements, results for one set-up can be transferred to other set-ups, if the waveguide aperture (ratio of the waveguide width a and the waveguide height b) remains constant. A connection at frequency f and with a flange tolerance t exhibits the same repeatability as a waveguide connection at frequency 2f and with a flange tolerance $t/\mathrm{2}$. Figure 9 shows two misaligned waveguides of the same size, their potential displacement or misalignment and the resulting parasitic effects.

To achieve high precision measurements, special flange adapters shown in Fig. 10 were designed at PTB. They allow accurate translations in steps of 0.3 mm in both directions using alignment pins in the alignment matrices on the left and right side of the waveguide interface. The measurement setup consists of a standalone VNA, coaxial adapters to R 140 and these special flange adapters. As VNA calibration TRL is chosen. For the simulation a simple approach is taken. The background material is set to perfect electric conductor (PEC) and the waveguides are modeled as boxes made of vacuum for simplicity. The waveguide ports are then deembedded to the discontinuity. The results agree very good with simulations from METAS (10⁻⁴ or better) available in METAS VNA Tools (Federal Institute of Metrology (METAS), 2024).

4.2 Simulation and Measurement Results

In the following diagrams the results of measurement and simulation for three cases are discussed: Fig. 11 summarized translation in horizontal direction Δx and Fig. 12 shows translation in vertical direction Δy. To assess the effect of combinations in vertical and horizontal misaligned, Fig. 13 summarized the special case of Δx=Δy.

As discussed in Marcuvitz (1986, p. 298 f.), a horizontal misalignment leads to a parasitic shunt inductance as shown in Fig. 9 and denoted by L(Δy). The characteristic impedance of the waveguide, denoted as Z₀, is altered by the presence of the shunt inductance admittance X to $Z_{\mathrm{0}}^{\prime }$. According to Marcuvitz (1986, p. 303 f.), the ratio $Z_{\mathrm{0}}^{\prime }/Z_{\mathrm{0}}$ is greater than 1. As misalignment increases, so does the magnitude of inductance and the mismatch of $Z_{\mathrm{0}}^{\prime }$, resulting in increased reflection and reduced transmission as seen in Fig. 11. This phenomenon has a more pronounced impact at lower frequencies compared to higher frequencies because the impedance X=j 2πfL of the shunt inductance linearly scales with frequency f and inductance L. At lower frequencies, $Z_{\mathrm{0}}^{\prime }$ tends to Z₀ and the influence of the misalignment decreases.

In the case of vertical misalignment, as illustrated in Fig. 9 and denoted by C(Δx), a parasitic capacitance is observed. As shown in Marcuvitz (1986, p. 309) the shunt admittance B=j 2πfC transforms the characteristic admittance Y₀ to $Y_{\mathrm{0}}^{\prime }$. As misalignment increases, so does the magnitude of capacitance and the mismatch of $Y_{\mathrm{0}}^{\prime }$, resulting in increased reflection and reduced transmission. Inversely to the horizontal misalignment, the phenomenon increases for higher frequencies, because the shunt admittance scales linearly with frequency f and capacitance C.

Looking at the special case of identical translation in x and y, Fig. 13 shows steep resonances in reflection. These resonances at around 13.5 GHz are the result of a parasitic inductance and capacitance caused by the misalignment of the two waveguide interfaces in vertical and horizontal direction (Marcuvitz, 1986, p. 298 f. and 309 f.). Together they form a parallel resonant circuit with resonance frequency f_r≈13.5 GHz. At this frequency, the combined parasitic effect of L and C cancel out each other. Therefore, the discontinuity behaves akin to a Thru connection. This is only the case, if the misalignment in vertical and horizontal direction are equal to each other, meaning Δx=Δy. For other combinations, the resonance frequency changes or lies out of band completely. The difference between measurement and simulation is always smaller than $\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{3}}$ for the real part and smaller than $\mathrm{10}\times {\mathrm{10}}^{-\mathrm{3}}$ for reflection and transmission coefficients. Relating this to the reported CMC values discussed in Sect. 3, a good agreement is observed.

5 Conclusions

In this study, a systematic analysis of measurement uncertainties stemming from rectangular waveguide calibrations was undertaken. The uncertainty budget for different waveguide bands was thoroughly examined and the significance of individual uncertainty contributions was discussed in detail. The analysis revealed that connection repeatability exerts a significant impact. Consequently, an in-depth investigation into the effects of misaligned waveguide interfaces was conducted. The study underscores the importance of precisely aligned waveguide interfaces, as evidenced through simulation and experimental data.