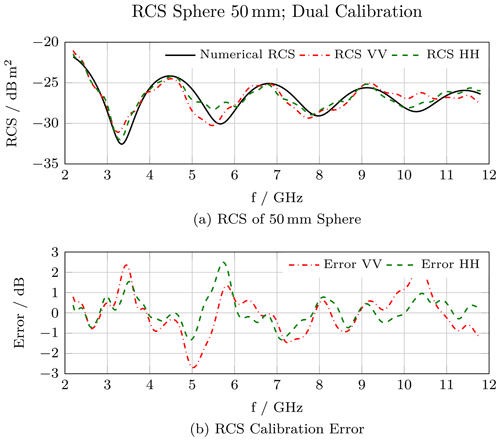
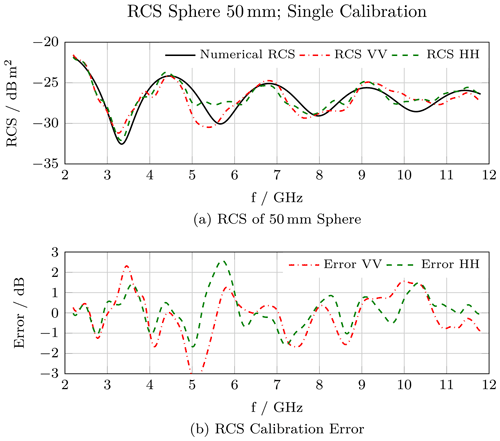
Compact Radar Cross-Section Measurement Setup and Performance Evaluation

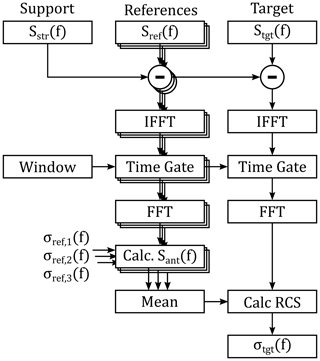
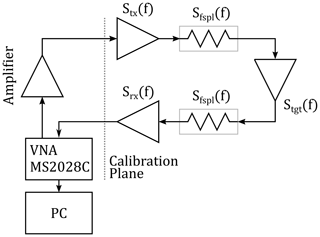
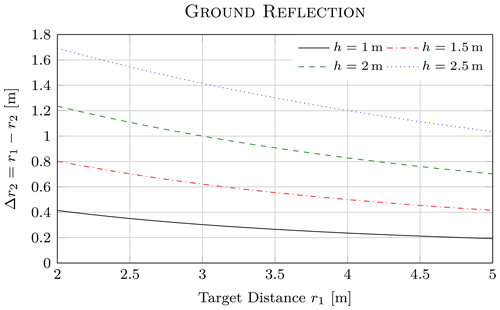
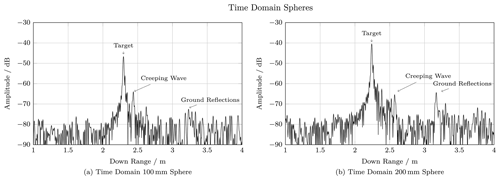
Radar cross-section measurements require the background reflections to be much lower than the reflections of the device under test. Although, anechoic chambers with special target holders meet this requirement, they are expensive and still have imperfections. To further reduce background reflections or to measure in environments where an anechoic chamber is not suitable, digital signal processing can be used to reduce background reflections. In this paper, a complete signal processing chain realized in Matlab is proposed, involving time gating of the measured target response and a background subtraction technique. Furthermore, the proposed signal processing includes a calibration procedure with either a single known calibration target or multiple known targets to improve measurement uncertainties. A compact measurement setup, consisting of a vector network analyzer and two horn antennas, is used to evaluate the overall performance and the advantages of a multiple known target calibration in a practical manner. The calibrated setup is able to measure the radar cross-section in a frequency range from 2 to 12 GHz with a mean error of less than 0.2 dB for both, VV and HH polarization combinations. It could also be shown, that a multi target calibration can result in an improvement of the measurement uncertainty by about 2.5 %.

1 Introduction

The radar cross-section (RCS) is the equivalent area of an isotropic reflector, that reflects the same amount of power than the target of investigation. The RCS varies over frequency, polarization and over the angle of incidence for a monostatic radar and thus is a good entity to describe reflection properties of targets in a radar scene. Although, the RCS is well calculable for simple target geometries, more complex structures need to be measured. These structures could be for example dynamic clutter or structures which are randomly structured and hard to describe in a model. For this reason, an inexpensive yet compact measurement setup has been developed and is presented in this work. The setup consists of a vector network analyzer (VNA) and two close arranged broadband horn antennas. The measurement bandwidth of the system is limited by the bandwidth of the horn antennas and ranges from 2 to 12 GHz.

A crucial issue of RCS measurements is the effort to minimize reflections not coming from the device-under-test (DUT). The RCS measurement error is mainly determined by the ratio of the reflected power of the DUT and the power coming from environmental reflections, as given by Eq. (1) from Chufeng et al. (2016). Where ϵ is the ratio of target reflected power to reflection power caused by the measurement environment.

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }\mathit{\sigma }=-\mathrm{20}\log \left(\mathrm{1}-{\mathrm{10}}^{\frac{-\mathit{ϵ}}{\mathrm{20}}}\right)\end{array}$$

Assuming the RCS measurement uncertainty should be 1 dB, then the echo power from the environment must be 20 dB below the DUT reflected power. It is difficult to meet this requirement for small targets, hence low RCS, so that measurements are usually done in anechoic chambers with elaborately constructed target holders. In some situations anechoic chambers are not suitable or unpractical due to their size and cost, so that signal processing can be used to suppress unwanted reflections. This is done by time gating and a background subtraction technique presented in Sect. 3.

Also, the calibration of the RCS measurement setup has a big impact on the measurement uncertainty. It is a common technique to calibrate RCS measurements with a known target, often spheres and cylinders are used. Even small imperfections of the calibration target can result in significant measurement uncertainty. So to improve the calibration quality, a multi target calibration procedure is presented and the advantages are compared to a single target calibration.

2 RCS Measurement Setup

The proposed system uses two adjacent positioned broadband horn antennas and a VNA to measure the ratio of reflected power versus transmitted power. In Fig. 1 the horn antennas and VNA are mounted on a tripod, making it a compact and transportable unit. The antennas are mounted so that they can be rotated to measure at different polarisations. In this contribution the VV and HH polarisation is used, meaning vertical polarisation of the transmit and receive antenna (VV) and horizontal polarisation of the transmit and receive antenna (HH). The system needs to be calibrated separately for both polarisation setups. The DUT is mounted on an expanded polystyrene (EPS) foam column, that is used as a target support structure. Truncated EPS foam cones provide low RCS and therefore are suitable as RCS support structures as discussed by Berrie and Wilson (2003).

Figure 1 Compact RCS measurement unit and 400 mm diameter calibration sphere placed on an expanded polystyrene foam column.

3 RCS Calculation

The complete signal processing of a target RCS over frequency calculation is seen in Fig. 2. First, the response without a DUT is measured (S_str) to gain information of the reflections caused by the environment and the support structure. Then, the responses of one or multiple calibration reference targets with known RCS are measured (S_ref) and finally the DUT is measured (S_tgt).

Figure 2 RCS measurement processing chain. At least three measurements are required: (1) measurement of support structure for background cancellation, (2) measurements of known reference targets and (3) the response of the DUT. The endproduct is the RCS over frequency response.

S_str is subtracted from the reference and target responses, to eliminate reflections caused by the support structure and the static environment. Also, the cross-talk of the adjacent antennas is reduced, as the cross-talk can be seen as static in between measurements and only changes slightly with a DUT in the scene. This technique is referred as background subtraction, more about this can be found by Svegi et al. (2013).

In a next step, multipath reflections need to be eliminated, otherwise they would interfere with the reflection of the DUT and be noticeable as ripple in the RCS over frequency measurement result. Because multipath reflections arrive later than the direct path reflection, a bandpass time gate is applied to the responses. This is realized by transforming the measured complex valued, bandpass characteristic responses into the time domain. Then, a four-term Blackman-Harris window is used to gate the target at a given range. The width of the gate is chosen, such that multipath reflections are filtered out and that the width is at minimum approximately the circumference of the DUT. Then, the gated impulse response is transformed back in the frequency domain.

The gated response S_gated is now only superimposed of the antenna response, the response of the free space propagation paths and the reflection response of the DUT, as seen in Fig. 3.

Figure 3 Measurement setup block diagram, involving transmission responses of the antennas, free space paths and target reflection response. The VNA along with the amplifier are phase and amplitude calibrated and thus not considered in the system response equation. Furthermore, unwanted reflections are already filtered out by background subtraction and time gating.

The overall system response equals the two-way monostatic radar equation given in Eq. (2) (Skolnik, 2008). The overall antenna response is combined as S_ant=S_txS_rx.

$$\begin{array}{}\text{(2)}& S_{\mathrm{gated}}\left(f\right)=S_{\mathrm{ant}}\left(f\right)S_{\mathrm{fspl}}\left(f{)}^{\mathrm{2}}{S}_{\mathrm{tgt}}\right(f)\end{array}$$

The free space path response is defined in Eq. (3). It includes the phase shift due to the propagation distance between the DUT and the antennas.

$$\begin{array}{}\text{(3)}& S_{\mathrm{fspl}}\left(f\right)={\displaystyle \frac{c}{\mathrm{4}\mathit{\pi }rf}}\exp \left(-j\mathrm{2}\mathit{\pi }r{\displaystyle \frac{f}{c}}\right)\end{array}$$

The target reflection response S_tgt(f) is rearranged to the common RCS entity with Eq. (4). The target response is not quadrated to obtain the phase information of the scatterer, see Knott et al. (2004, p. 72).

$$\begin{array}{}\text{(4)}& \sqrt{\mathit{\sigma }}\left(f\right)=\sqrt{A_{\mathrm{iso}}}{S}_{\mathrm{tgt}}\left(f\right)={\displaystyle \frac{c}{\mathrm{2}\sqrt{\mathit{\pi }}f}}{S}_{\mathrm{tgt}}\left(f\right)\end{array}$$

Equations (2) and (4) combined lead to the complex valued RCS of the DUT.

$$\begin{array}{}\text{(5)}& \sqrt{\mathit{\sigma }}\left(f\right)={\displaystyle \frac{c}{\mathrm{2}\sqrt{\mathit{\pi }}f}}{\displaystyle \frac{S_{\mathrm{gated}}\left(f\right)}{S_{\mathrm{ant}}\left(f\right){S_{\mathrm{fspl}}}^{\mathrm{2}}\left(f\right)}}\end{array}$$

The residual unknown response S_ant(f) is calculated using the reference target responses. With the measured response and the known response of the reference, the antenna response can be calculated as in Eq. (6). After calculating the antenna response for every reference target, the arithmetic mean of the antenna response is calculated.

$$\begin{array}{}\text{(6)}& S_{\mathrm{ant}}\left(f\right)={\displaystyle \frac{S_{\mathrm{gated}}\left(f\right)}{{S_{\mathrm{fspl}}}^{\mathrm{2}}\left(f\right)}}{\displaystyle \frac{c}{\mathrm{2}\sqrt{\mathit{\pi }}f\sqrt{\mathit{\sigma }}\left(f\right)}}\end{array}$$

References used in this paper are stainless steel spheres with different diameters. Spheres are good references in terms of nearly non-existent cross-polarization and they are isotropic reflectors. Also, the RCS of a sphere is well calculable by the Mie solution of the maxwell equations, see Mahafza (2005). Using different sized calibration standards to obtain S_ant(f) and calculating the mean afterwards reduces the measurement error introduced by the calibration process, as noise power in the reference measurements will be reduced and calibration target imperfections will be averaged. The advantage of multiple target calibration will be discussed in Sect. (5).

4 Ground Reflection Considerations

The only strong expected undesired scattering near the DUT is caused by ground reflections. If the antenna height and the target distance is chosen properly, the ground reflections can be filtered out in the time domain.

In Fig. 4 are the distances of the next ground reflection to the direct target reflection for different antenna heights. The target is positioned in the same height as the antennas. r₁ is the target distance, r₂ is the shortest path from the target to the antennas over the ground plus r₁ and then is divided by two to convert to down range.

Figure 4 Distance of next ground reflection Δr₂ to direct target reflection r₁ for different antenna heights. Antennas and Target are at the same height.

Depending on how wide the time gate is, the target distance and antenna height can be chosen to get a good discrimination of the desired target reflection from the ground reflection. But with decreasing r₁, the measurement uncertainty can grow due to near field phase errors, see Sect. (5) for further information.

Furthermore, the ground surface roughness should be as flat as possible. Any perturbation can be seen as a peak in the time domain and results in an uncertainty in the final RCS result.

Figure 5 Time Domain response of 100 mm sphere (VV-measurement) in panel (a) and 200 mm sphere (VV-measurement) in panel (b). Data has been zero-padded before inverse Fourier transformation to improve range resolution.

5 RCS Measurement Results

Measurements were done to evaluate the performance of the proposed signal processing. The measurements were performed inside an empty laboratory room, as seen in Fig. 1. The VNA swept from 2 to 12 GHz, resulting in a range resolution of 15 mm. The targets were placed about 2.5 m away from the antennas. Because the RCS needs to be measured in the far-field, it follows that the DUT has to be excited with a plane wave. Assuming that the transmit antenna is a point source and the transmitted wave propagates in a spherical shape towards the DUT, the DUT should not be larger than the radius calculated with Eq. (7) to meet the far-field criterion, see Balanis (2016). Given the target distance is r=2.5 m and the maximum phase error due to spherical wave propagation should be smaller than $\mathrm{\Delta }r=\frac{\mathit{\lambda }}{\mathrm{8}}$ for the highest frequency (in our case 12 GHz), the radius of the DUT should be smaller than z=250 mm.

$$\begin{array}{}\text{(7)}& r\approx {\displaystyle \frac{z^{\mathrm{2}}}{\mathrm{8}\mathrm{\Delta }r}}\text{with}\mathrm{\Delta }r={\displaystyle \frac{\mathit{\lambda }}{\mathrm{8}}}\Rightarrow r\approx {\displaystyle \frac{z^{\mathrm{2}}}{\mathit{\lambda }}}\end{array}$$

Figure 5 depicts the time domain measurement of a 100 and 200 mm sphere with background subtraction. The time is transformed into down range by multiplying the time axis with $\frac{c_{\mathrm{0}}}{\mathrm{2}}$. The target peak is followed by a smaller peak that is produced by delayed creeping waves. Creeping waves occur for sphere circumferences that are in the range of the wavelength and are responsible for the typical wave-like RCS behavior in this wavelength region. Further away, one can slightly see multipath reflections caused by the DUT to ground interaction. These reflections will be filtered out after the range gate filter.

To compare different calibration standards and methods with each other, the dual-calibration difference metric introduced and used by Kent (2001) is an entity to monitor the quality of RCS calibration measurements. It uses two targets whose RCS are accurately known. One target is used to calibrate the system and the other serves as a reference target to monitor the calibration error. The error or dual-calibration difference metric is then calculated by dividing the measured RCS of the reference target with the numeric RCS.

In Fig. 6a one can see the measured RCS of a 50 mm sphere as well as the numerical RCS. Also, the calibration error is plotted in Fig. 6b. The system was calibrated using a 200 and 100 mm calibration sphere and calculating the mean of both calibration terms. The standard deviation of the VV-measurement error is 1.0 dB and for the HH-measurement 0.7 dB. The mean error for both measurements is less than 0.1 dB.

Figure 6 RCS measurement results of 50 mm calibration sphere for VV and HH polarisation (a) and deviation in dB from numerical value (b). The system was calibrated with 200 and 100 mm spheres using the mean of the resulting calibration terms.

Because the time gating with a window function causes great distortion at the band edges in the frequency domain, as discussed by De Porrata-Doria i Yague et al. (1998), the first and last 40 samples are discarded. The distortion can be shifted outside the frequency band of interest by extrapolating the time domain data, but is not done in this paper, due to the wide measurement bandwidth anyway.

For comparison, the measurement was evaluated with the system calibrated with a single 100 mm sphere in Fig. 7. The standard deviation is now slightly greater. For the VV-measurement error it is 1.1 and 0.85 dB for the HH-measurement. The mean error for both measurements is now 0.15 dB.

Figure 7 RCS measurement result of 50 mm calibration sphere for VV and HH polarisation using a single 100 mm sphere for calibration (a) and deviation in dB from numerical value (b).

In conclusion there is only a slight improvement by using two calibration targets versus a single calibration target. Because any huge imperfection of one calibration target, meaning it deviates from the numerical RCS a lot, is only improved slightly by the second calibration target. The spheres used in this paper are hollow stainless steel spheres that consist of two hemispheres that are welded together. The construction results in a cheap sphere, but also in a flat spot around the welding and thus an imperfection in the spherical shape. This results in a deviation from the theoretical sphere model and explains the only slight benefit from using two calibration standards versus single calibration standard procedure.

6 Conclusion

A compact and yet simple RCS measurement setup was presented and it has been shown that even small target RCS can be measured with an acceptable range of measurement uncertainty. The background subtraction and time gating algorithms were able to sufficiently suppress static clutter of the environment, antenna cross-talk and target support structure reflections. By carefully setting up the range to the DUT and the height of the antennas, respectively the height of the DUT, multipath reflections caused by ground reflections can also be suppressed by the time gate.

Furthermore, the advantage of a multi reference target calibration has been shown and compared to a single reference target calibration measurement. The improvement was considered weak, about 2.5 % less uncertainty, and the reason was found to be not perfectly spherical shaped calibration standards. So the importance of accurate calibration targets was emphasized.

Appendix A: Equation abbreviations

Stx, Srx	Tx/Rx Antenna Response
Sfspl	Free Space Path
Stgt	Target Reflection
Sgated	Gated System Response
σref,i	ith Numerical Calibration Target RCS
r	Distance of DUT
c	Propagation Speed
h	Height of Antennas