Calculations of electromagnetic fields in longitudinal irregular TEM-cells

TEM-cells can be used as a standardized field generator for field probe calibration purposes or electromagnetic compatibility measurements. Because of its practical use as a measurement environment, the electromagnetic behavior over a broad range of frequencies is essential. However, without the understanding of wave reflection, mode-conversion, and attenuation, using such a measurement environment is impractical. In this contribution, we calculate the electromagnetic fields in a longitudinal irregular coaxial TEM-cell. Using a semi-analytical approach, we can determine these wave characteristics. The method is based on the projection of Maxwell's equations onto eigenfunctions. This work's primary objective is to examine the effect of irregular deformed boundaries on the electromagnetic field and the resonance frequencies.

1 Introduction

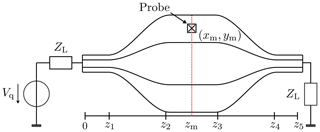
An often-used field generator is the TEM-cell, a closed coaxial transmission line (Groh et al., 1999), as shown in Fig. 1. For reproducible electromagnetic compatibility (EMC) results, a suitable measurement environment and a particular field polarization are needed. It is desirable to measure the field strengths in the so-called far-field region. The fundamental mode in a TEM-cell is the TEM-mode; above a specific frequency f_c (cutoff frequency), waveguide modes (TM and TE) start to propagate. So one primary downside is the upper-frequency limit. The TEM-cell consists of a uniform section tapered at each end to adapt to standard coaxial connectors (see Fig. 2). Usually, the TEM-cell is designed as a 50 Ω impedance-matched system to ensure minimum reflection of the operating TEM-mode. Due to the tapered sections, the waveguide modes will reflect at both ends. Thus, the TEM-cell forms a highly resonating structure. Another disadvantage compared to an open site or anechoic chamber is the limited test volume within the cell. Nevertheless, the electromagnetic (EM) field is well defined and sufficiently uniform to be useful in the calibration of EM field probes or EMC measurements. Higher frequency operation is achieved with a smaller TEM-cells cross-section 𝒮, but it also reduces the testing volume. The TEM-cell is used for creating a known EM field in which a field probe is calibrated for use as transfer standards or general-purpose field probes. Because such probes are usually small in their dimensions, and their calibration requires a very well-defined field, TEM-cells are a suitable field generator. A circular coaxial TEM-cell is of simple construction and basically an enlarged transmission line; it is also a portable measurement environment in its smaller versions (see Fig. 5).

However, practical TEM-cells are usually not uniform due to the geometry, e.g., surface roughness or tolerances in the manufacturing process. An efficient approach to calculate the EM fields in nonuniform waveguides is a semi-analytical method known as Generalized Telegraphist's Equations (GTEs). The GTEs and related methods of transverse cross-sections (also known as Coupled-mode theory and cross-section method) are widely used in the theory of waveguides with longitudinally varying boundaries (Shafii and Vernon, 1995; Vlasov and Antonsen, 2001; Maksimenko et al., 2019). By converting Maxwell's equations with appropriate boundary conditions (BCs), we obtain ordinary differential equations of the transmission line type (Schelkunoff, 1952). Expanding the EM fields into an orthogonal series of basis functions, an infinite system of differential equations is derived. Sporleder and Unger (1979), Huang and Hung-Chia (1984), and Katsenelenbaum et al. (1998) have published comprehensive monographs on this method. The previously mentioned works are mostly limited to waveguides with simply connected cross-sections.

Fliflet and Read (1981) originally derived the GTEs for coaxial waveguides. Koch (1999) has made the first attempt to thoroughly investigate closed TEM-Cells (Crawford- and GTEM-cells) using GTEs. The mode coupling mechanism in an ideal coaxial TEM-cell with circular cross-section has been investigated, and numerical results were shown in Pham and Garbe (2020). Because the GTEs can not directly calculate the resonance frequencies f_r of the TEM-cells, an approximated method was presented in Pham et al. (2020).

In this contribution, the GTEs are used to investigate the effects of mechanical tolerances on the electromagnetic fields in coaxial TEM-cells. Therefore, the numerical results of the GTEs are verified by comparing them with a commercially available field simulator (CST Studio) and field measurements in a TEM-cell with similar geometric dimensions. The knowledge can be used in the design process of the TEM-cell to reduce mode-coupling and field uncertainties. In addition, the contribution of the field generator (TEM-cell) to the measurement uncertainty of electromagnetic fields can be determined, which is of great importance during field probe calibration.

First of all, we briefly introduce the theoretical formalism of the approach in Sect. 2. In Sect. 3, the irregular boundaries are modeled, and all relevant equations and parameters are derived. Following, Sects. 4 and 5, all numerical results are shown and discussed. The conclusion in Sect. 6 gives a summary of the most important insights of this contribution.

Figure 1 Geometry of TEM-cell and schematic representation of measurement setup. The probe is located at ${\mathit{r}}_{\mathrm{m}}=\left(x_{\mathrm{m}},y_{\mathrm{m}},z_{\mathrm{m}}\right)$.

Table 1 Simulation Parameters.

Figure 2 Longitudinal view of the tapered section of coaxial TEM-cell.

2 Generalized Telegraphist's Equations

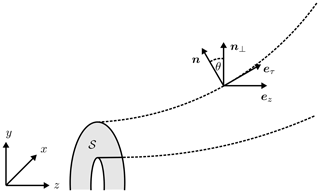
As mentioned above, we concisely review the GTEs in this section, following prior published work (Pham and Garbe, 2020). To derive the GTEs for a two-port coaxial TEM-cell (see Fig. 1), we introduce a set of appropriate orthogonal coordinates $\left(u,v,z\right)$. u and v are transverse coordinates, and for convenience, the z-axis coincides with the TEM-cells z-axis (see Fig. 2). We limit our analyses to an empty TEM-cell with the electric and magnetic constants (ε,μ). Next, we decompose the EM field vectors (E,H)

$$\begin{array}{}\text{(1)}& \mathit{E}={\mathit{E}}_{⟂}+{\mathit{E}}_z,\mathit{H}={\mathit{H}}_{⟂}+{\mathit{H}}_z,\end{array}$$

and the Nabla operator ∇

$$\begin{array}{}\text{(2)}& \mathrm{\nabla }={\mathrm{\nabla }}_{⟂}+{\mathit{e}}_z{\displaystyle \frac{\partial }{\partial z}},\end{array}$$

into transverse and longitudinal parts. $\left({\mathit{E}}_{⟂},{\mathit{H}}_{⟂}\right)$ and (E_z,H_z) are the transverse and longitudinal field amplitudes, and ∇_⟂ is the Nabla operator for the transverse coordinates. We assume harmonic time dependence, and therefore the term e^jωt (ω=2πf, carrier frequency) is omitted in all sequential equations. The transverse components of Maxwell's equations define E_⟂ and H_⟂ (Reiter, 1959)

$$\begin{array}{}\text{(3a)}& {\displaystyle \frac{\partial {\mathit{E}}_{⟂}}{\partial z}}=\mathrm{j}\mathit{\omega }\mathit{\mu }\left({\mathit{e}}_z\times {\mathit{H}}_{⟂}\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{j}\mathit{\omega }\mathit{\epsilon }}}{\mathrm{\nabla }}_{⟂}\left({\mathrm{\nabla }}_{⟂}\left({\mathit{H}}_{⟂}\times {\mathit{e}}_z\right)\right),\text{(3b)}& {\displaystyle \frac{\partial {\mathit{H}}_{⟂}}{\partial z}}=\mathrm{j}\mathit{\omega }\mathit{\epsilon }\left({\mathit{E}}_{⟂}\times {\mathit{e}}_z\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{j}\mathit{\omega }\mathit{\mu }}}{\mathrm{\nabla }}_{⟂}\left({\mathrm{\nabla }}_{⟂}\left({\mathit{e}}_z\times {\mathit{E}}_{⟂}\right)\right).\end{array}$$

Both transverse field components E_⟂ and H_⟂ will be expanded into a series of orthogonal vector functions (e,h). The transverse fields are represented at each axial location as a sum of the fundamental TEM-mode and the waveguides modes (TM- and TE-mode) with a transverse cross-section 𝒮 equal to the local cross-section of the reference TEM-waveguide. We have a solution in the following form

$$\begin{array}{}\text{(4a)}& {\displaystyle }{\mathit{E}}_{⟂}=V_{\mathrm{0}}^{\text{TEM}}{\mathit{e}}_{\mathrm{0}}^{\text{TEM}}+\sum _{n=\mathrm{1}}^{\mathrm{\infty }}{V}_n^{\text{TM}}{\mathit{e}}_n^{\text{TM}}+V_n^{\text{TE}}{\mathit{e}}_n^{\text{TE}},\text{(4b)}& {\displaystyle }{\mathit{H}}_{⟂}=I_{\mathrm{0}}^{\text{TEM}}{\mathit{h}}_{\mathrm{0}}^{\text{TEM}}+\sum _{n=\mathrm{1}}^{\mathrm{\infty }}{I}_n^{\text{TM}}{\mathit{h}}_n^{\text{TM}}+I_n^{\text{TE}}{\mathit{h}}_n^{\text{TE}},\end{array}$$

where (e_n,h_n) are the eigenvector fields of the reference TEM-waveguide's electric and magnetic fields. The single subscript n in Eq. (4b) is considered a double subscript pq, where

$$\begin{array}{}\text{(5)}& p\in {\mathbb{N}}_{\mathrm{0}}:=\mathbb{N}\cup \left\{\mathrm{0}\right\},q\in \mathbb{N}\end{array}$$

To avoid the double summation expression, we will use the single subscript. For brevity, we will omit the index (TM, TE, and TEM) and distinguish between the different waveguide modes by enclosing the subscripts in parentheses (n) for TM-modes and in brackets [n] for TE-modes. The basis amplitudes (V_n(z),I_n(z)) are functions of the coordinate z. The eigenvector fields (e,h) in Eq. (4b) can be obtained by

$$\begin{array}{}\text{(6a)}& {\displaystyle }{\mathit{e}}_{\left(n\right)}& {\displaystyle }=-{\mathrm{\nabla }}_{⟂}{\mathrm{\Pi }}_{\left(n\right)},& {\displaystyle }{\mathit{h}}_{\left(n\right)}& {\displaystyle }={\mathit{e}}_z\times {\mathit{e}}_{\left(n\right)},\text{(6b)}& {\displaystyle }{\mathit{e}}_{\left[n\right]}& {\displaystyle }={\mathit{h}}_{\left[n\right]}\times {\mathit{e}}_z,& {\displaystyle }{\mathit{h}}_{\left[n\right]}& {\displaystyle }=-{\mathrm{\nabla }}_{⟂}{\mathrm{\Pi }}_{\left[n\right]},\text{(6c)}& {\displaystyle }{\mathit{e}}_{\mathrm{0}}& {\displaystyle }=-{\mathrm{\nabla }}_{⟂}{\mathrm{\Pi }}_{\mathrm{0}},& {\displaystyle }{\mathit{h}}_{\mathrm{0}}& {\displaystyle }={\mathit{e}}_z\times {\mathit{e}}_{\mathrm{0}},\end{array}$$

where Π(u,v) is the scalar wavefunction (Marcuvitz, 1951). The different mode's scalar wavefunctions Π are determined by the following differential equations (Helmholtz and Laplace equation) and BCs

$$\begin{array}{}\text{(7a)}& {\displaystyle }\left({\mathrm{\nabla }}_{⟂}^{\mathrm{2}}+k_{\left(n\right)}^{\mathrm{2}}\right){\mathrm{\Pi }}_{\left(n\right)}& {\displaystyle }=\mathrm{0},& {\displaystyle }{\mathrm{\Pi }}_{\left(n\right)}& {\displaystyle }={\left.\mathrm{0}\right|}_{\partial \mathcal{S}},\text{(7b)}& {\displaystyle }\left({\mathrm{\nabla }}_{⟂}^{\mathrm{2}}+k_{\left[n\right]}^{\mathrm{2}}\right){\mathrm{\Pi }}_{\left[n\right]}& {\displaystyle }=\mathrm{0},& {\displaystyle }{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\left[n\right]}}{\partial \mathit{n}}}& {\displaystyle }={\left.\mathrm{0}\right|}_{\partial \mathcal{S}},\text{(7c)}& {\displaystyle }{\mathrm{\nabla }}_{⟂}^{\mathrm{2}}{\mathrm{\Pi }}_{\mathrm{0}}& {\displaystyle }=\mathrm{0},& {\displaystyle }{\mathrm{\Pi }}_{\mathrm{0}}& {\displaystyle }={\left.C\right|}_{\partial \mathcal{S}},\end{array}$$

where ${\mathrm{\nabla }}_{⟂}^{\mathrm{2}}$ denotes the Laplacian to the transverse coordinates. The term k_n in Eqs. (7a) and (7b) describes the eigenvalue of the nth TM- or TE-mode.

The Poynting vector describes the power of the EM field. Concerning the orthogonality properties (9) and the series expansion (4b), we get

$$\begin{array}{}\text{(8)}& {\displaystyle }\begin{array}{rl}{S}_z& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{\mathcal{S}}{\int }\left({\mathit{E}}_{⟂}\times {\mathit{H}}_{⟂}^{*}\right){\mathit{e}}_z\mathrm{d}S\\ & ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\sum ^{\mathrm{\infty }}}_n{V}_n\cdot I_n^{*}\underset{\mathcal{S}}{\int }{\mathit{e}}_n^{\mathrm{2}}\mathrm{d}S\end{array}.\end{array}$$

The surface integral is to be extended over the TEM-waveguide cross-section 𝒮 at z (see Fig. 2). We use the above expression (8) to simplify the entire representation and choose the eigenvector fields (e_n,h_n) to satisfy the orthogonality condition

$$\begin{array}{}\text{(9)}& \underset{\mathcal{S}}{\int }\left({\mathit{e}}_n\times {\mathit{h}}_{\mathrm{m}}\right){\mathit{e}}_z\mathrm{d}S=T_n^{\mathrm{2}}{\mathit{\delta }}_{mn},{\mathit{\delta }}_{mn}=\left\{\begin{array}{cc}\mathrm{0}& m\ne n\\ \mathrm{1}& m=n\end{array}\right.,\end{array}$$

where δ_mn is the Kronecker delta function, and

$$\begin{array}{}\text{(10)}& T_n^{\mathrm{2}}=\underset{\mathcal{S}}{\int }{\mathit{e}}_n^{\mathrm{2}}\mathrm{d}S=\underset{\mathcal{S}}{\int }{\mathit{h}}_n^{\mathrm{2}}\mathrm{d}S\end{array}$$

is a normalization factor (Marcuvitz and Schwinger, 1951).

We use Maxwell's transverse components Eq. (3b), the modal expansion (4b), and the orthogonality condition (9) to derive the GTEs. Taking the projection on Maxwell's equations onto the eigenvector fields (e,h) results in an infinite set of ordinary differential equations (Vlasov and Antonsen, 2001)

$$\begin{array}{}\text{(11a)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{V}_{\mathrm{m}}}{\mathrm{d}z}}=& -\mathrm{j}{\mathit{\gamma }}_{\mathrm{m}}{Z}_{\mathrm{m}}{I}_{\mathrm{m}}+\sum _n^{\mathrm{\infty }}{V}_n\underset{\mathcal{S}}{\int }{\mathit{e}}_{\mathrm{m}}{\displaystyle \frac{\partial {\mathit{e}}_n}{\partial z}}\mathrm{d}S\\ & +\underset{\partial \mathcal{S}}{\oint }{E}_{\mathit{\tau }}{\mathit{n}}_{⟂}{\mathit{e}}_{\mathrm{m}}\mathrm{d}L\end{array}\text{(11b)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{I}_{\mathrm{m}}}{\mathrm{d}z}}=& -\mathrm{j}{\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{m}}}{Z_{\mathrm{m}}}}{V}_{\mathrm{m}}-\sum _n^{\mathrm{\infty }}{I}_n\underset{\mathcal{S}}{\int }{\mathit{e}}_n{\displaystyle \frac{\partial {\mathit{e}}_{\mathrm{m}}}{\partial z}}\mathrm{d}S\\ & -{\displaystyle \frac{\mathrm{1}}{\mathrm{j}\mathit{\omega }\mathit{\mu }}}\underset{\partial \mathcal{S}}{\oint }\left({\mathit{e}}_z\times {\mathit{E}}_{⟂}\right){\mathit{n}}_{⟂}{\mathrm{\nabla }}_{⟂}{\mathit{h}}_{\mathrm{m}}\mathrm{d}L\end{array}\end{array}$$

in which γ_m is the propagation constant and Z_m the wave impedance of the respective mode

$$\begin{array}{}\text{(12a)}& {\displaystyle }{\mathit{\gamma }}_{\mathrm{0}}& {\displaystyle }=\mathrm{j}\mathit{\omega }\sqrt{\mathit{\epsilon }\mathit{\mu }},& {\displaystyle }{Z}_{\mathrm{0}}& {\displaystyle }=\sqrt{{\displaystyle \frac{\mathit{\mu }}{\mathit{\epsilon }}}},\text{(12b)}& {\displaystyle }{\mathit{\gamma }}_{\left(m\right)}& {\displaystyle }=\sqrt{k_{\left(m\right)}^{\mathrm{2}}-{\mathit{\omega }}^{\mathrm{2}}\mathit{ϵ}\mathit{\mu }},& {\displaystyle }{Z}_{\left(m\right)}& {\displaystyle }={\displaystyle \frac{{\mathit{\gamma }}_{\left(m\right)}}{\mathrm{j}\mathit{\omega }\mathit{\epsilon }}},\text{(12c)}& {\displaystyle }{\mathit{\gamma }}_{\left[m\right]}& {\displaystyle }=\sqrt{k_{\left[m\right]}^{\mathrm{2}}-{\mathit{\omega }}^{\mathrm{2}}\mathit{ϵ}\mathit{\mu }},& {\displaystyle }{Z}_{\left[m\right]}& {\displaystyle }={\displaystyle \frac{\mathrm{j}\mathit{\omega }\mathit{\mu }}{{\mathit{\gamma }}_{\left[m\right]}}}.\end{array}$$

The surface integrals on the right-hand side of Eq. (11b)

$$\begin{array}{}\text{(13)}& C_{mn}=\underset{\mathcal{S}}{\int }{\mathit{e}}_{\mathrm{m}}{\displaystyle \frac{\partial {\mathit{e}}_n}{\partial z}}\mathrm{d}S,C_{nm}=\underset{\mathcal{S}}{\int }{\mathit{e}}_n{\displaystyle \frac{\partial {\mathit{e}}_{\mathrm{m}}}{\partial z}}\mathrm{d}S,\end{array}$$

describe the effect of axial variations of the transverse cross-section 𝒮 (Reiter, 1959). The remaining line integrals in Eq. (11b) involve the tangential electric field at the boundary ∂𝒮. For the current case, we restrict our analysis to perfectly conducting TEM-cells (perfect electric conductor, PEC). Therefore, both terms become equal to zero using cylindrical coordinates $\left(u=r,v=\mathit{\phi },z\right)$ and substituting the BCs (${\left.\mathit{n}\times \mathit{E}=\mathbf{0}\right|}_{\partial \mathcal{S}}$, PEC) into the integral kernel of Eq. (11b) (see Fig. 2)

$$\begin{array}{}\text{(14a)}& {\displaystyle }O& {\displaystyle }=\underset{\partial \mathcal{S}}{\oint }\left(E_z+\tan \left(\mathit{\theta }\right)E_r\right){\mathit{n}}_{⟂}{\mathit{e}}_{\mathrm{m}}\mathrm{d}L=\mathrm{0},\text{(14b)}& {\displaystyle }P& {\displaystyle }=\underset{\partial \mathcal{S}}{\oint }-E_{\mathit{\phi }}{\mathrm{\nabla }}_{⟂}{\mathit{h}}_{\mathrm{m}}\mathrm{d}L=\mathrm{0}.\end{array}$$

The preceding Eq. (11b) apply to either TM-, TE-, or TEM-modes. A more detailed derivation of the GTEs can be seen in Marcuvitz and Schwinger (1951). In Pham and Garbe (2020), the mode coupling mechanism due to longitudinal variations of the geometry was reduced to TM_0q- and TEM-mode coupling.

An analytical expression for the coupling coefficients C can be derived from the normalized eigenvector fields of a uniform coaxial TEM-waveguide. In our case, the coupling coefficients in Eq. (13) can be further simplified. We use the following boundary conditions for the scalar wavefunction Π (Solymar, 1959)

$$\begin{array}{}\text{(15)}& \mathrm{\Pi }={\left.-\tan \left(\mathit{\theta }\right){\displaystyle \frac{\partial \mathrm{\Pi }}{\partial {\mathit{n}}_{⟂}}}\right|}_{\partial \mathcal{S}},{\displaystyle \frac{\partial \mathrm{\Pi }}{\partial z}}={\left.-\tan \left(\mathit{\theta }\right){\displaystyle \frac{\partial \mathrm{\Pi }}{\partial z\partial {\mathit{n}}_{⟂}}}\right|}_{\partial \mathcal{S}},\end{array}$$

to reduce the surface integrals in Eq. (13) to line integrals over the cross-section's 𝒮 perimeter (Fliflet et al., 1980; Shafii and Vernon, 1995)

$$\begin{array}{}\text{(16a)}& {\displaystyle }{C}_{\left(n\right)\left(m\right)}& {\displaystyle }=C_{\left(m\right)\left(n\right)}=F_{\mathrm{1}}\left(z\right)\underset{\partial \mathcal{S}}{\oint }{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\left(n\right)}}{\partial {\mathit{n}}_{⟂}}}{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\left(m\right)}}{\partial {\mathit{n}}_{⟂}}}\mathrm{d}L,\text{(16b)}& {\displaystyle }{C}_{\left(m\right)\left(m\right)}& {\displaystyle }=F_{\mathrm{2}}\left(z\right)\underset{\partial \mathcal{S}}{\oint }{\left({\displaystyle \frac{\partial {\mathrm{\Pi }}_{\left(m\right)}}{\partial {\mathit{n}}_{⟂}}}\right)}^{\mathrm{2}}\mathrm{d}L,\text{(16c)}& {\displaystyle }{C}_{\mathrm{0}\left(m\right)}& {\displaystyle }=C_{\left(m\right)\mathrm{0}}=\mathrm{2}{F}_{\mathrm{2}}\left(z\right)\underset{\partial \mathcal{S}}{\oint }{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\mathrm{0}}}{\partial {\mathit{n}}_{⟂}}}{\displaystyle \frac{\partial {\mathrm{\Pi }}_{\left(m\right)}}{\partial {\mathit{n}}_{⟂}}}\mathrm{d}L,\text{(16d)}& {\displaystyle }{C}_{\mathrm{00}}& {\displaystyle }=F_{\mathrm{2}}\left(z\right)\underset{\partial \mathcal{S}}{\oint }{\left({\displaystyle \frac{\partial {\mathrm{\Pi }}_{\mathrm{0}}}{\partial {\mathit{n}}_{⟂}}}\right)}^{\mathrm{2}}\mathrm{d}L\end{array}$$

with

$$\begin{array}{}\text{(17a)}& {\displaystyle }{F}_{\mathrm{1}}\left(z\right)& {\displaystyle }=\tan \left(\mathit{\theta }\left(z\right)\right){\displaystyle \frac{k_{\left(m\right)}^{\mathrm{2}}\left(z\right)}{k_{\left(m\right)}^{\mathrm{2}}\left(z\right)-k_{\left(n\right)}^{\mathrm{2}}\left(z\right)}},\text{(17b)}& {\displaystyle }{F}_{\mathrm{2}}\left(z\right)& {\displaystyle }=-{\displaystyle \frac{\tan \left(\mathit{\theta }\left(z\right)\right)}{\mathrm{2}}}.\end{array}$$

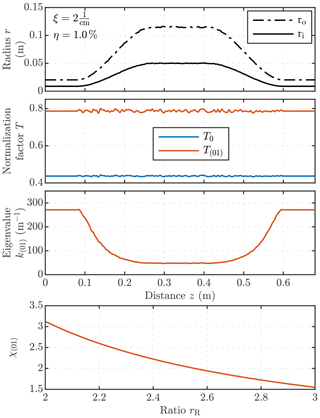
Figure 3 One implementation of a longitudinal irregularly deformed TEM-cell and the resulting normalization factors (T₀,T₍₀₁₎) and the eigenvalue k₍₀₁₎. The terms ξ and η define the frequency and the amplitude of the perturbation along the TEM-cell. Below, the root χ₍₀₁₎ of the TM₀₁-mode as a function of the ratio r_R is shown.

3 Irregular boundary

According to Pham and Garbe (2020), TEM-cell's mode-coupling mechanism with longitudinal variations in the cross-section 𝒮 can be reduced to only interactions between TEM- and TM_0q-modes. As long as the outer and inner radius ratio r_R is constant along the z axis, no reflection of the operating TEM-mode occurs, and the coefficient in Eq. (16c) is zero. There is also no coupling to any higher-order TE-mode.

In Sect. 2, explicit formulas of the coupling coefficients were derived (see Eq. 16d). In the case of a longitudinal irregular TEM-cell, these coefficients do not change significantly. Due to the irregular inner and outer radius, the ratio

$$\begin{array}{}\text{(18)}& r_{\mathrm{R}}\left(z\right)={\displaystyle \frac{r_{\mathrm{a}}\left(z\right)}{r_{\mathrm{i}}\left(z\right)}}\end{array}$$

varies along the z axis. Hence the characteristic impedance

$$\begin{array}{}\text{(19)}& Z_{\mathrm{L}}\left(z\right)={\displaystyle \frac{Z_{\mathrm{0}}}{\mathrm{2}\mathit{\pi }\sqrt{\mathit{\epsilon }}}}\ln \left(r_{\mathrm{R}}\left(z\right)\right)\end{array}$$

is not constant, which causes reflections of the operating TEM-mode. The coefficient C₀₀ in Eq. (16c) becomes unequal zero. Another important fact is that the TM-modes eigenvalues

$$\begin{array}{}\text{(20)}& k_{\left(pq\right)}\left(z\right)={\displaystyle \frac{{\mathit{\chi }}_{\left(pq\right)}\left(z\right)}{r_{\mathrm{i}}\left(z\right)}}\end{array}$$

and both normalization factors

$$\begin{array}{}\text{(21a)}& {\displaystyle }{T}_{\mathrm{0}}\left(z\right)& {\displaystyle }={\left(\mathrm{2}\mathit{\pi }\ln \left(r_{\mathrm{R}}\left(z\right)\right)\right)}^{-\frac{\mathrm{1}}{\mathrm{2}}},\text{(21b)}& {\displaystyle }{T}_{\left(pq\right)}\left(z\right)& {\displaystyle }=\sqrt{{\displaystyle \frac{\mathit{\pi }}{\mathrm{2}{\mathit{ϵ}}_p}}}{\left({\displaystyle \frac{J_p\left({\mathit{\chi }}_{\left(pq\right)}\left(z\right)\right)}{J_p\left({\mathit{\chi }}_{\left(pq\right)}\left(z\right)r_{\mathrm{R}}\left(z\right)\right)}}\right)}^{-\frac{\mathrm{1}}{\mathrm{2}}}\end{array}$$

with

$$\begin{array}{}\text{(22)}& {\mathit{ϵ}}_p=\left\{\begin{array}{c}\mathrm{2}p=\mathrm{0}\\ \mathrm{1}p>\mathrm{0}\end{array}\right..\end{array}$$

depend on the ratio r_R(z). To calculate χ_(pq) in Eq. (20), we need to compute the roots of the following equation (Marcuvitz, 1951)

$$\begin{array}{}\text{(23)}& {\displaystyle }\begin{array}{rl}\mathrm{0}& =N_p\left({\mathit{\chi }}_{\left(pq\right)}\left(z\right)\right)J_p\left({\mathit{\chi }}_{\left(pq\right)}\left(z\right)r_{\mathrm{R}}\left(z\right)\right)\\ & -J_p\left({\mathit{\chi }}_{\left(pq\right)}\left(z\right)\right)N_p\left({\mathit{\chi }}_{\left(pq\right)}\left(z\right)r_{\mathrm{R}}\left(z\right)\right).\end{array}\end{array}$$

In which J_p and N_p denote to Bessel- and Neumann functions. As an illustrative example of a longitudinal irregular TEM-cell, the outer and inner radius (r_o,i), the normalization factors (T₀,T₍₀₁₎), the eigenvalue k₍₀₁₎, and the root χ₍₀₁₎ are shown in Fig. 3. The radius r_o,i is only a function of z

$$\begin{array}{}\text{(24)}& r_{\mathrm{o},\mathrm{i}}=R_{\mathrm{o},\mathrm{i}}\cdot \left(\mathrm{1}+\mathit{\delta }\left(z\right)\right),\end{array}$$

where R_o,i is the radius of the ideal TEM-cell, and the function δ describes the random deformation of the boundary.

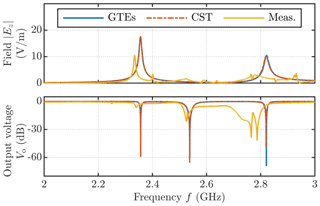
Figure 4 Magnitude of the longitudinal field component $\left|E_z\left(x_{\mathrm{m}},y_{\mathrm{m}},z_{\mathrm{m}}\right)\right|$ and the output voltage V_o as a function of the frequency $f=\left[f_{\mathrm{low}},f_{\mathrm{up}}\right]$.

Figure 5 Coaxial TEM-cell.

Figure 6 Simulation results of the basis amplitudes (V₀,V₍₀₁₎) and the magnitude of the radial field component $\left|E_{\mathrm{r}}\left(x_{\mathrm{m}},y_{\mathrm{m}},z\right)\right|$ in between r_o and r_i at two frequencies (f_low and f_up).

4 Numerical results

To solve the GTEs of a two-port TEM-cell (see Fig. 1), we need additional BCs for the respective mode's basis amplitudes (V,I). The following BCs apply to the TEM-cells's left and the right port for the TEM-mode basis amplitude V₀

$$\begin{array}{}\text{(25)}& V_{\mathrm{0}}={\left.V_{\mathrm{q}}-I_{\mathrm{0}}{Z}_{\mathrm{L}}\right|}_{z=\mathrm{0}},V_{\mathrm{0}}={\left.I_{\mathrm{0}}{Z}_{\mathrm{L}}\right|}_{z=z_{\mathrm{5}}}.\end{array}$$

For the basis amplitudes of the waveguide modes (TM and TE), the radiation conditions will be used at the TEM-cells in- and output (Fliflet and Read, 1981)

$$\begin{array}{}\text{(26a)}& {\displaystyle }{V}_{\left(n\right)}& {\displaystyle }={\left.Z_{\left(n\right)}{I}_{\left(n\right)}\right|}_{z=\mathrm{0}},& {\displaystyle }{V}_{\left[n\right]}& {\displaystyle }={\left.Z_{\left[n\right]}{I}_{\left[n\right]}\right|}_{z=\mathrm{0}},\text{(26b)}& {\displaystyle }{V}_{\left(n\right)}& {\displaystyle }={\left.-Z_{\left(n\right)}{I}_{\left(n\right)}\right|}_{z=z_{\mathrm{5}}},& {\displaystyle }{V}_{\left[n\right]}& {\displaystyle }={\left.-Z_{\left[n\right]}{I}_{\left[n\right]}\right|}_{z=z_{\mathrm{5}}}.\end{array}$$

Wave impedances are used in the GTEs (Eq. 11b). Therefore, the characteristic impedance Z_L needs to be substituted by the wave impedance Z₀ in the above BCs (Eq. 25). The relation between both terms can be obtained by Eq. (19). According to the normalization of the basis amplitudes and eigenvectors (see Eqs. 9–8), V_q also needs to be substituted by

$$\begin{array}{}\text{(27)}& V_{\mathrm{q}}^{\mathrm{TEM}}={\displaystyle \frac{V_{\mathrm{q}}}{K}}.\end{array}$$

For coaxial TEM-waveguides with a concentric circular cross-section 𝒮, the transformation factor K becomes

$$\begin{array}{}\text{(28)}& K=\sqrt{{\displaystyle \frac{\ln \left(r_{\mathrm{R}}\right)}{\mathrm{2}\mathit{\pi }}}}.\end{array}$$

Combining the two differential equations in Eq. (11b), we obtain the state space equation

$$\begin{array}{}\text{(29)}& {\displaystyle \frac{\mathrm{d}}{\mathrm{d}z}}\left[\begin{array}{c}\mathit{V}\\ \mathit{I}\end{array}\right]=\left[\begin{array}{cc}\underset{\mathrm{¯}}{\mathbf{C}}& \underset{\mathrm{¯}}{\mathbf{O}}\\ \underset{\mathrm{¯}}{\mathbf{P}}& -{\underset{\mathrm{¯}}{\mathbf{C}}}^{\top }\end{array}\right]\cdot \left[\begin{array}{c}\mathit{V}\\ \mathit{I}\end{array}\right].\end{array}$$

The explicit form of the above matrices $\left(\mathbf{C},\mathbf{O},\mathbf{P}\right)$ and vectors (V,I) can be found in Pham and Garbe (2020).

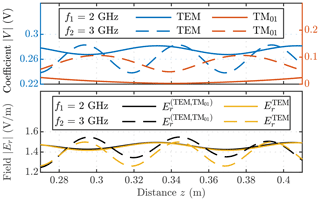
The infinite set of coupled differential equations (Eq. 29) is truncated and solved numerically by the finite difference method. In Pham and Garbe (2020), it has been shown that only four additional modes need to be considered in the frequency bandwidth $f_{\mathrm{b}}=\left[f_{\mathrm{low}},f_{\mathrm{up}}\right]$ for a coaxial TEM-cell with these geometric dimensions (see Fig. 1 and Table 2). Therefore, all our simulations were performed with N=4 modes. We have compared the longitudinal field component |E_z(r_m)| and the output voltage V_o=|V₀(z₅)| of the GTEs with numerical results of another software tool and measurements on a coaxial TEM-cell with similar geometric dimensions. For the electric field measurements, we have used an optical field probe system (ENprobe EFs-105). A schematic setup of the measurement is given in Fig. 1. All results are displayed in Fig. 4.

The magnitude of the basis amplitudes V₀,V₍₀₁₎ and V₍₀₂₎ for the upper and lower limit of our frequency bandwidth f_b is displayed in Fig. 7. Using the GTEs, the resonance frequencies f_r of the TEM-cell can be computed. We limited our simulations to a frequency step size of Δf=0.1 MHz, resulting in 10 001 frequency samples. The resonance frequencies f_r can be obtained by analyzing the output voltage V₀. Figure 8 shows the output voltage V₀ as a function of the frequency f at the second port of an ideal and three implementation of an irregularly deformed TEM-cell. The transverse EM fields can be determined according to Eq. (4b). An analog expression for the longitudinal fields can be obtained by substituting Eq. (4b) into Maxwell's Equations (see Pham and Garbe, 2020). Figure 9 shows the magnitude of the radial and longitudinal electric field component $\left(\left|E_{\mathrm{r}}\left(x_{\mathrm{m}},y_{\mathrm{m}},z\right)\right|,\left|E_z\left(x_{\mathrm{m}},y_{\mathrm{m}},z\right)\right|\right)$ as a function of the frequency $\left(f=\left[f_{\mathrm{low}},f_{\mathrm{up}}\right]\right)$ along the z axis. The electric field magnitude is shown below the waterfall plots at the first resonance frequency $\left(f_{{\mathrm{r}}_{\mathrm{1}}}\approx \mathrm{2.4}\mathrm{GHz}\right)$ along the radius r and the z axis.

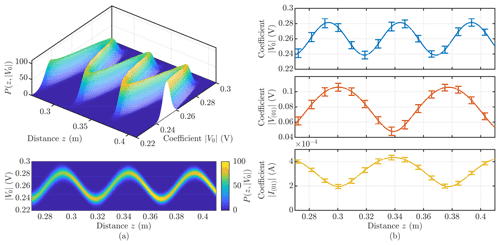
Using the GTEs, the basis amplitudes (V,I) for different implementations of longitudinal irregularly deformed TEM-cells can be calculated, and a local probability density function (PDF) for the basis amplitudes can be obtained. As a representative example, 10⁴ random implementations at f_up were computed. The local PDF of the basis amplitude V₀ is shown in Fig. 10a (only for the middle section of the TEM-cell). The mean value and the standard deviation of the basis amplitudes V₀,V₍₀₁₎ and I₍₀₁₎ are given in Fig. 10b.

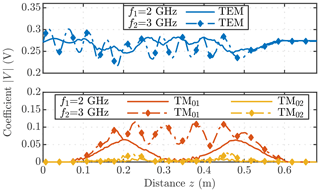
Figure 7 Simulation results of the basis amplitudes V₀,V₍₀₁₎ and V₍₀₂₎ at two different frequencies for an irregularly deformed TEM-cell.

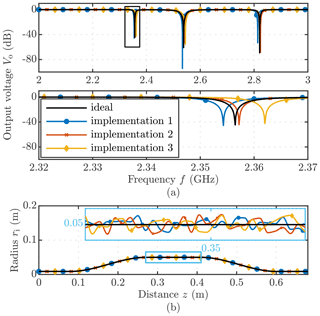
Figure 8 (a) Output voltage V_o at the second port (z=z₅) for an ideal and three implementation of an longitudinal irregularly deformed TEM-cell. (b) As an illustrative example three implementation of an longitudinal irregularly deformed inner radius r_i are shown. Because of the small deformation an additional zoom plot (blue box) is given for the middle section of r_i.

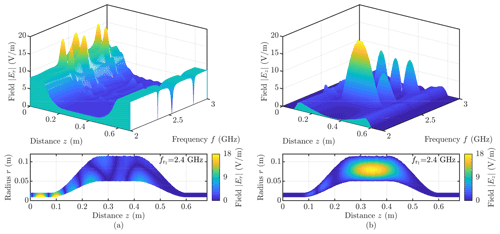
Figure 9 (a) Magnitude of the radial field component $\left|E_r\left(x_{\mathrm{m}},y_{\mathrm{m}},z\right)\right|$ in between r_o and r_i as a function of the frequency f. Below a cross-sectional view of |E_r(r,z)| at the first resonance frequency $f_{{\mathrm{r}}_{\mathrm{1}}}$. (b) Magnitude of the longitudinal field component $\left|E_z\left(x_{\mathrm{m}},y_{\mathrm{m}},z\right)\right|$ in the center between r_o and r_i as a function of the frequency f. Below a cross-sectional view of |E_z(r,z)| at the first resonance frequency $f_{{\mathrm{r}}_{\mathrm{1}}}$.

Figure 10 (a) Local probability function of the basis coefficient V₀ as a function of the distance z. (b) Mean value and standard deviation of the basis amplitudes V₀,V₍₀₁₎ and I₍₀₁₎ as a function of the distance z.

5 Discussion of numerical results

Before examining the effect of longitudinal irregularly deformed boundaries on the EM fields and the resonance frequencies $f_{{\mathrm{r}}_i}$, we verified our numerical results of the GTEs for an ideal and regular TEM-cell.

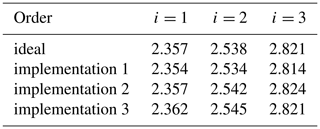
Table 2 Resonance frequencies $f_{{\mathrm{r}}_i}$ (GHz) of the TM₀₁-mode in a coaxial TEM-cell with circular cross-section.

First, we compared the numerical results of the GTEs with simulations of commercially available software (CST Studio Suite 2019). The magnitude for the longitudinal electric field component |E_z(r_m)| and the output voltage V_o=|V₀(z₅)| are in good agreement. Second, we conducted measurements on a TEM-cell with similar geometric dimensions (see Fig. 5). We can see some differences between the numerical results (GTEs and CST) and the measurements. Most likely due to various uncertainties during the measurement setup, e.g., position and alignment of the field probe, which have not been considered. The geometric uncertainties significantly impact the EM fields and resonance frequencies; for example, the tapering length and the coaxial connectors differ from our simulation model. Another critical factor is that we have limited our analyses to PEC, so all losses were neglected in the GTEs. Hence, the shift of the resonance frequencies $f_{{\mathrm{r}}_i}$ is partially due to ohmic losses.

The obtained numerical results confirm strong mode-conversion from the operating TEM-mode to the TM₀₁-mode, mostly in the tapered sections (see Fig. 7). Above the TM₀₁-mode's cutoff frequency f_c, the basis amplitude V₍₀₁₎ has a considerable magnitude and can not be neglected. In Fig. 6, the effect of the TM₀₁-mode on the radial field component E_r becomes apparent. A simple approximation of the radial field is possible since the basis amplitude V₀ is dominant for most frequencies, except for the resonance frequencies (see Fig. 9). Due to the irregular boundaries, local coupling to higher-order TM_0q-modes occurs throughout the TEM-cell. The deformed boundaries impact the course of the basis amplitudes and hence the field distribution (see Figs. 7 and 9). However, only the first propagating TM₀₁-mode affects the middle section field because all basis amplitudes of the non-propagating modes are negligibly small. Additionally, we also have an impact on the resonance frequencies. A slight shift of all three resonance frequencies $f_{{\mathrm{r}}_i}$ (up to 7 MHz) is notable (see Fig. 8 and Table 2).

6 Conclusions

In this contribution, the EM field and the resonance frequencies in a longitudinal irregular coaxial TEM-cell have been calculated using the GTEs. First of all, the coupling coefficients revealed the TEM-mode's effective mode-conversion in the tapered sections of the TEM-cell. Due to the irregular longitudinal boundaries along the TEM-cell, local excitation of the higher-order modes occurs. The magnitude of the coupling depends on the frequency. All calculations have been performed for a cylindrical TEM-cell with a circular cross-section, and numeric results were presented. The effect of irregularly deformed boundaries on the field and the resonance frequencies were shown. Comparable simulations and measurements on a coaxial TEM-cell with similar geometric dimensions have been performed to verify the results of the GTEs. Using the GTEs, we can calculate a local probability density function for the EM fields in the TEM-cell. Hence an uncertainty contribution due to the geometric tolerances of TEM-cell can be defined. The results can be used during the designing process of the TEM-cell to prevent higher-order mode coupling or estimate the uncertainty contribution of the field generator for a field probe calibration.