Signal degradation through sediments on safety-critical radar sensors
Matthias G. Ehrnsperger
Uwe Siart
Michael Moosbühler
Emil Daporta
Thomas F. Eibert
This paper focusses on a transmission line (TL) based model which allows to investigate the impact of multilayered obstructions in the propagating path of a radar signal at different distances and in combination with disturbances. Those disturbances can be water, snow, ice, and foliage at different densities, temperatures, positions, with a given thickness and layer combination. For the evaluation of the detectability of objects, the impulse response of the system can be obtained. Investigations employing state-of-the-art radar hardware confirm the consistency of theoretical and experimental results for 24 and 77 GHz. The analysis in this paper supports testing the specifications for radar systems, before carrier frequency and antenna layout are finally decided. Thereby, the radar system parameters can be adjusted toward employed carrier frequency, bandwidth, required sensitivity, antenna and amplifier gain. Since automotive standards define operational environmental conditions such as temperature, rain rate, and layer thickness, these parameters can be included and adapted. A novel optimisation methodology for radomes is presented which allows to boost the dynamic range by almost 6 dB with presence of a worst-case cover layer of water. The findings can be utilised to properly design radar systems for automotive applications in autonomous driving, in which other vulnerable road users have to be protected under all circumstances.
- Article
(4543 KB) - Full-text XML
- BibTeX
- EndNote
During the last decade radar systems have experienced a renaissance with a broad field of new applications. The first automotive radar system was employed in the 1960s, nowadays all middle class and above vehicles are equipped with at least one radar system. For these radar systems, mostly two frequencies are utilised: 24 GHz for short range radar (SRR) and 77 GHz for long range radar (LRR). Another frequency is already making its way into the automotive sector: 5.8 GHz. Especially safety and monitoring applications are adapting the emerging C-band systems. The most promising advantages of 5.8 GHz are material penetration capabilities, reduced environmental impairment due to water, and – most important – low-cost availability. The main differences between the three frequencies (5.8, 24, and 77 GHz) are not only the associated regulations, but also their fundamentally different behaviour in varying environments. Especially the signal attenuation due to absorption, reflection, and interference is highly frequency-dependent. What matters the most in the automotive and safety sector is the resiliency of a system, so that reliable operation can be guaranteed at any time. For arising radar applications in the automotive and safety field, protective sensors for people and machinery are often subject to external installation and, hence, also to pollution, icing, and wetness. Especially critical safety systems must not be operationally affected in any way but secure safety at all times. Hence, adverse environmental influences should be assessed beforehand, to ensure a sufficiently designed radar system.
Radar sensors are advantageous for the recognition and detection of moving or static objects – most notably living objects – within a predefined vicinity, area, or space. Usually radar systems are assembled in a locally protected environment to avoid signal debasing sediments. However, externally installed safety-critical radar-based sensors in disadvantageous assembly positions are becoming more and more popular. For living object protection (LOP) and living object detection (LOD), the sensors face two major challenges: first, safety-critical sensor systems have – by definition – to be operational at all times, to ensure maximum safety, and second, since an external installation has to be taken into consideration, the resulting environmental influences must be evaluated and operationability must be self-tested. By way of illustrating such scenarios, Fig.1a and b show an operative radar sensor under good weather conditions (Fig. 1a), which may fail under different weather conditions such as rain (Fig. 1b).
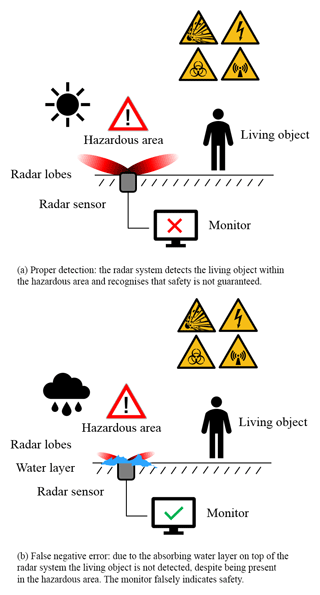
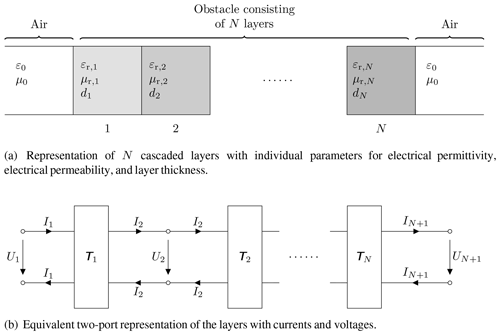
Figure 1Visualisation of a safety-critical radar system that is mounted in a disadvantageous manner, hereby flush mounted in the ground. The sensor is exposed to environmental influences, which are schematically represented by the water layer. The size of the radar lobes schematically indicates the signal strength and therefore the detection probability. The monitor symbolises a general evaluation unit which handles the received signals and displays the result, whether or not an object is detected.
As a matter of fact, the detection of an object can only be successful if a signal is received. For this purpose, radomes are generally employed to protect the system. These radomes shall not affect the antenna characteristics nor the transceived signal in any way. Depending on the system, generally a signal is transmitted and the reflection of objects within the propagation path of the electromagnetic wave is processed. The received signals must be sufficiently strong to be employable. The radar equation,
is helpful to estimate the received signal power. Hereby, Pr is the power of the received signal, Pt is the power of the transmitted signal, Gt and Gr are the gains of the transmitter and receiver, respectively, λ is the free-space wavelength, σ is the radar cross section (RCS) of the object, Rt and Rr are the distances from the transmitter and receiver to the object, respectively. For a monostatic radar system, where the transmitted and received signal both are transferred by the same antenna, the equation simplifies with , and . The last term LA represents the general losses of the system. Those can result due to all sorts of geometrical, system, and climatic influences. Since externally installed radar systems are mainly affected by weather events, in the following, the focus to evaluate LA is based on climatic influences. The signal-to-noise ratio (SNR) describes how well a signal can be distinguished from noise. If LA increases as a result of sediments or the like, the decreases, whereby N represents the overall noise level. As the SNR decreases, so does the probability of a successful detection. In consequence the false alert rate increases which significantly affects the system performance and may lead to a raised customer frustration and endangerment level.
In order to simulate an electromagnetic wave propagating through space with obstacles and discontinuities, usually full wave solvers are utilised. For reasonably accurate results of the full wave solution, even a small volume requires a considerable processing power. As a trade-off of the required computational power and time, as well as the accuracy of results, the obstacles are approximated as infinitely extended homogeneous layers that consist of the individual obstacle material, as illustrated in Fig. 2a. Single obstacle layers do not exist in reality and are of no interest, hence, an obstacle within the model consists of N individual material layers. The parameters of each layer are the relative electric permittivity (εr,n) and the relative electric permeability (μr,n), the geometrical parameter is the thickness (dn). This layer-based obstacle model is then transformed into a transmission line based equivalent circuit. Hereby, each one of the layers is transformed into an equivalent two-port, see Fig. 2b. In consequence, not the E- and H-fields are calculated, instead, the model relies on voltages and currents. The model is based on normal plane wave propagation only, without refraction, oblique incidence, scattering, and polarisation effects. The fundamental basis is provided by the impedance concept of Schelkunoff (1951).
2.1 Expectable climatic and external impacts
Based on empirical investigations, the expectable climatic and external influences are: liquid water, as closed or continuous water layers with and without interruptions, individual drops, and condensation; dry or wet snow; fully-frozen ice layers, crystallised local spots; dry or wet foliage layers or individual leaves; moist or wet dirt, dust, and sedimentation layers.
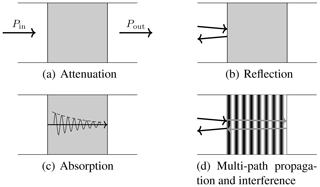
In general, when a signal is transmitted towards an obstacle, reflection, absorption, and interference attenuate the power that penetrates the obstacle itself (Fig. 3a). The electromagnetic power of a wave is partially reflected at the obstacle boundaries (Fig. 3b), partially absorbed (Fig. 3c), and affected by multi-path propagation and interference (Fig. 3d). These effects are also taken into consideration within the layer based model as well as the equivalent transmission line (TL) model.
2.2 Electromagnetic material characteristics
The quality of a model is highly dependent on the underlying data. The data for the aforementioned expectable climatic influences (water, snow, ice, foliage, dirt) has been investigated theoretically and partially verified by measurements. In the following the datasets of each medium are presented.
2.2.1 Electromagnetic properties of water
The implementation of the complex permittivity of water is based on the model of Liebe et al. (1991). Hereby, assuming a time convention ejωt the complex permittivity is represented by
where the subscript “W” indicates water. The parameters are the static relative permittivity εs, the asymptotic relative permittivity for very high frequencies ε∞, and the resonant frequency of the molecular vibration fd. εs is temperature-dependent according to
and its calculation is based on experimental results. The temperature dependency is
where the temperature is defined from about 0 to 40 ∘C. The remaining parameters are calculated as
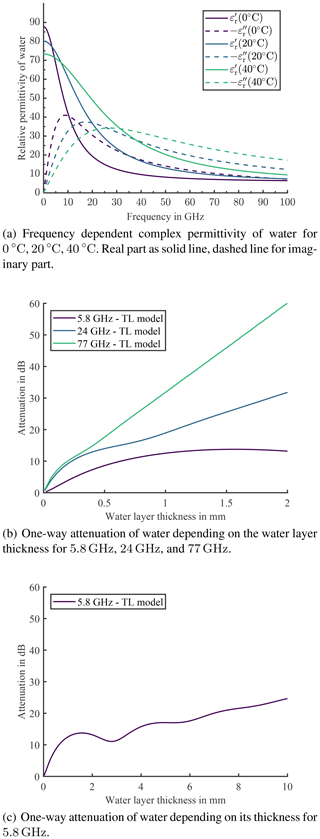
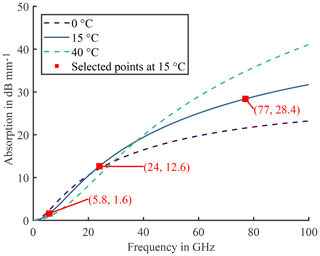
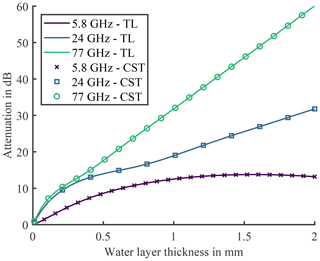
Even though such data is available in the given references, the complex permittivity of water at various temperatures can be observed in Fig. 4a. Hereby, the solid line represents the real part of εr, the dashed line the imaginary part. The values have been printed for three different temperatures: 0, 20, 40 ∘C. Upon closer inspection of the imaginary part, it becomes obvious that the temperature has a significant impact on the position of the maximum. Over the 40 ∘C temperature shift, the resonance frequency spreads over more than 20 GHz. This result substantiates the large impact of the temperature. In Fig. 4b, the one-way attenuation in dB of a homogeneous water layer is plotted for thicknesses up to 2 mm at 15 ∘C. Hereby, the three frequencies of interest are shown, 5.8, 24, and 77 GHz. The aforementioned effect of interference can be nicely observed for the 5.8 GHz graph, since the attenuation first increases, but then, for an increased thickness of the water layer begins to decrease. Therefore, in Fig. 4c the one-way attenuation for 5.8 GHz is plotted for a water layer thickness of up to 10 mm. Here, the effect of interference is even more evident. For 24 and 77 GHz the attenuation graphs show a linear tendency starting at comparatively low water layer thicknesses, yet, for 5.8 GHz the effects of interference are more dominant so that a linear approximation is only applicable for a thicker layer. To employ valid approximations of the attenuation graphs, the equations of Table 1 can be employed for increased layer thickness values. In Fig. 5 the one-way attenuation versus the frequency is shown. The three frequencies of interest are highlighted with its corresponding attenuation offset, which is part of the equations of Table 1. To further illustrate the vast influence of the temperature, the dashed lines in Fig. 5 indicate the scope of the attenuation values. Upon further investigation, it can be observed that the higher the frequency, the larger the effect of the temperature on the attenuation.
2.2.2 Electromagnetic properties of ice
The dielectric behaviour of ice differs significantly from that of water. If water turns into ice, the dipole molecules are bound in a solid lattice structure, so that the reorientation is largely prevented. Therefore, the real part and the imaginary part of the complex permittivity of ice are smaller than of liquid water with freely polarisable molecules. A possible model for the dielectric permittivity of ice is given in Arage et al. (2006). This proposed model is suitable for temperatures in the range of −40 to 0 ∘C (Hallikainen, 2014). The relative permittivity of ice can be determined by
where the subscript “I” stands for ice. The individual parameters are further stated as
Here, α has the unit GHz and β has the unit GHz−1, T is the temperature in ∘C for the valid range of −40 to 0 ∘C. The resulting complex permittivity of ice has an approximate constant real part of 3.15 and a small imaginary part. The latter, however, may increase when ice is contaminated. According to Shuji et al. (1993), chemical impurities can even occur in natural ice in the form of salts and acids. In Shuji et al. (1997), for example, winter-typical contaminants such as sodium chloride (NaCl), nitroxyl (HNO) are examined in more detail. Concentrations between 10−5 and 10−3 mol dm−3 at a frequency of 5 GHz even led to a tenfold increase in the imaginary part of the relative dielectric permittivity. However, the values are still small. Dry ice as flat layers are far less critical than water. When the layer of ice thaws, the resulting water layer has far more impact than the ice itself. With ice, there is also the danger that an inhomogeneous layer thickness or a partial covering with ice could cause diffraction effects of the electromagnetic waves, which leads to distortions in the antenna characteristics (Pfeiffer, 2010).
2.2.3 Electromagnetic properties of snow
Snow can be classified as dry or wet, where both consist of three main components: air, ice, and water. Dry snow has very little impact upon electromagnetic waves, since the density is low and absorption is almost not present. The opposite is the case for wet snow. Wet snow has a higher density and consists of dry snow on the one hand, and a water volume fraction on the other hand. The water volume fraction with its freely polarisable molecules is mainly causing the attenuation of snow.
Dry snow
The composition of dry snow is a mixture of air and ice. Since the real part of the dielectric permittivity of ice corresponds to a constant, see Eq. (7), and is therefore independent of temperature and frequency (in the considered frequency range), it follows that the real part of the dielectric permittivity of dry snow is also independent of the temperature and frequency. According to Martti et al. (1989), is a function that depends only on the density of the dry snow ρDS. As a corresponding model
is considered in the following, where represents the real part of the dielectric permittivity of ice and corresponds to 3.15, further with ρi=0.916. For the calculation for the imaginary part of the permittivity of dry snow
is employed. Since and are independent of the temperature and frequency, the ratio is also characterised by this property. Due to the theoretical investigation of dry snow, in combination with the measurements of Martti et al. (1989), Ari et al. (1985), and Tiuri et al. (1984) this dielectric loss factor of dry snow is even lower than the already low loss factor of ice. Thus, the impact of dry snow on radar signals can be concluded as negligible.
Wet snow
According to Ari et al. (1985), the complex permittivity of wet snow is composed of two parts, namely the sum of the permittivity of dry snow, which in turn is composed of the dielectric permittivity of air and ice, and the excess permittivity due to liquid water in the snow, which of course depends on the dielectric permittivity of water. The relative complex permittivity of wet snow εr,WS can also be approximated by a model, the “modified Debye-Near model” presented in Martti et al. (1989). The model determines the dielectric permittivity as
Here, f is the valid frequency (f≤37 GHz), f0 is the relaxation frequency, is the volume fraction of water (percentage content of liquid water). The variables A, B, C, and x are chosen as
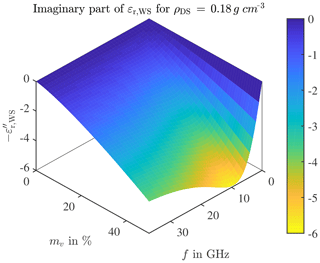
Different densities of dry snow components only result in a very small effect on the complex permittivity, a higher density results only in a slightly higher offset of the permittivity values. Accordingly, the values of the permittivity are primarily determined by the water content. This can also be recognised by the fact that the larger the volume fraction of water in the snow, the greater the dielectric permittivity of the water in weight, so that the permittivity of wet snow is greatly increased. The gradients of permittivities of wet snow and water have a high qualitative consistency. This fact allows a qualitative evaluation of the expected complex permittivity even for the out-of-definition frequency (Matzler et al., 1984). Snow covers in the centimetre range are a serious limitation for a reliably functioning radar system. In Fig. 6, the real part of the complex permittivity of wet snow is plotted, in Fig. 7 the corresponding imaginary part. The data represents the material constellation with density ρDS=0.18 g cm−3 the water volume fraction mv in % and the frequency f in GHz.
2.2.4 Electromagnetic properties of foliage
Similar to snow, foliage can also be considered as a mix of different components. The components in this case correspond to high permittivity water, low to moderate permittivity organic material, and air. Matzler (1994) provides a model for the dielectric permittivity. This was designed for foliage of different plant species and provides information about its impact on electromagnetic waves. From this, the dielectric permittivity of foliage is given as
where the subscript “F” indicates foliage and where the fraction of dry matter is valid for
which is defined
Here, md is the dry foliage matter and Mg represents the gravimetric water content. The given model is suitable for frequencies from 1 to 100 GHz. Consequently, εr,F is only dependent of the water content and the dielectric permittivity of water εr,W. εr,F is independent of the density of foliage, also the model is better suited for fresh foliage masses. In a dry foliage mass, the water content decreases, so that the loss of water, the dielectric properties or the real and imaginary part of the complex permittivity of leaves decrease. In addition, it is shown that the permittivity is very much dependent on the water content contained in the fresh foliage (Matzler, 1994). Studies of different models have shown that small volumes of air trapped in the water have a strong impact on dielectric properties (Matzler, 1994). The featured model also includes the modelling of water, however, without the salinity of the water in the foliage. This salinity is about one percent, depending on the season and deciduous species and is neglected due to the very low impact.
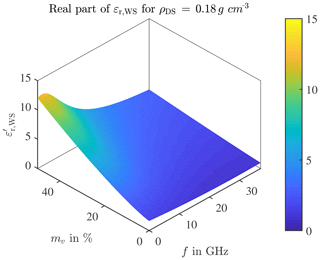
Figure 6Real part of complex permittivity of wet snow for a dry snow density ρDS=0.18 g cm−3 depending on the water volume fraction mv in % and the frequency f in GHz.
2.2.5 Electromagnetic properties of dirt
Dirt can also be considered as a four-component dielectric mixture, which is composed of soil solids, air, bulk water (free, unbound earth water) and bound water (Myron et al., 1985). Jun et al. (2013) has created a model which takes into account a more precise composition of soil solids and subdivides these into clay, silt and sand, with the dielectric permittivity of the soil dependent on the percentage of organic matter. However, the permittivity strongly depends on the free volume water. If a small volume of water is present in the dirt and it is increased, the dielectric permittivity is only slightly elevated. This is the result of the fact that, in addition to the mixture, added unbound water is to some extent transformed into bound water. This means that the added water molecules are not as freely repolarisable as the free volume of water. However, if continued to increase the percentage volumetric water content, it reaches a saturation point, from which much more water is taken up from the ground in the form of bound, but the proportion of free volume water is increased. As a result, the dielectric permittivity increases faster. Soil compositions with a larger organic matter content can absorb more water, resulting in a later saturation point and thus reach a higher level of bound water. These insights are based on the texts given in the bibliography (Quan et al., 2013; Myron et al., 1985; Schmugge et al., 1978; Mironov et al., 2004; Ansari and Evans, 1982; Chen and Ku, 2012; Jun et al., 2013; Vladimir, 1994; Wolfgang and Speckmann, 2004). In summary, dry soils have a real and imaginary part of the complex dielectric permittivity that is close to unity. These increase only with a volumetrically increasing water content. From this it can be concluded that some gravel, soil and similar earth compositions occurring on the concreted, paved, and otherwise pretreated areas do not significantly disturb the radar systems.
2.3 Computational performance
To verify the correctness and the performance of the TL model, the calculated results are compared to Computer Systems Technology (CST) Microwave Studio (MWS). Hereby, a general purpose time domain solver, the transient solver which is based on the finite integration technique (FIT), of CST MWS has been utilised. In the simulation the air-water-air layer constellation has been excited with a linearly polarised plane wave. What can be observed from Fig. 8 is, that both results from the TL model and from CST MWS agree to an acceptable extent. Since the test configuration is a single homogeneous dielectric layer that is illuminated by a plane wave, the comparison not only shows the correctness of the analytical vs. the numerical solution, but also their correct implementation. Comparing the required calculation power, taken into consideration that the TL model does not provide the extensive potential of CST MWS, the TL model calculates the same result significantly faster (equal workstation HP-Z840 employed for calculations).
According to Fig. 1, a safety-critical radar sensor system is taken into consideration in the following. The surveillance system monitors a hazardous area, which is unproblematic under standard weather conditions. Climatic influences affect the radar sensor performance due to absorption of energy. The solution is to minimise the impact of absorbing or reflecting layers within a predefined range, all that goes beyond these limitations results in blindness of the sensor. There are several possible ways to overcome the effects of absorbing material, the most naive solution is to increase the transmitted power in such a way that the absorption is compensated. However, as the attenuation of water can easily reach high values, such an approach can only counteract insignificantly small covering layers. Especially for low-cost and cost-critical systems with little dynamic range, simply increasing the transmit power is a less favourable methodology. A more effective approach is to optimise the whole system. This means that not only the radome is optimised for maximum performance, but also the snow, dust, or water layer that is expectable and within the absolute maximum range is taken into account.
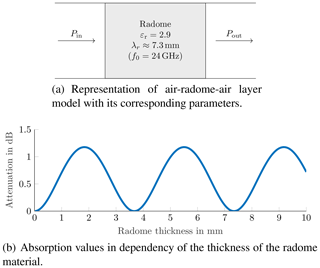
In the following a radar system at 24 GHz with a radome of polyoxymethylene (POM) is in focus. First of all, the radome is optimised in the traditional manner: in Fig. 9a the single layer radome is shown, its material parameters are the relative electrical permittivity of 2.9, the thickness of the layer is now evaluated. In the context of a layer-based model, the radome represents an air-radome-air system. The corresponding one-way attenuation of the layer composition can be seen in Fig. 9b, where the losses are almost zero and not taken into consideration in the following. In consequence, the attenuation in Fig. 9b varies between 0 and approximately 1.2 dB. The attenuation minima are located at radome thicknesses which are multiples of λr∕2, the attenuation maxima where the radome thickness is an odd multiple of λr∕4. Logically the radome thickness would be optimised to λr∕2 – hereby about 3.6 mm – to achieve maximum transmit power, minimised loss, and maximized performance.
However, the result changes if a perturbing layer on top of the radome is taken into consideration. As illustrated in Fig. 10a a uniform layer of water is placed on top of the radome material. The water layer has a constant thickness of 1 mm, which represents the absolute maximum for the given virtual application. The plot of Fig. 10b shows the total one-way attenuation versus the variation of the thickness of the radome material. The attenuation varies between about 16 dB and approximately 19 dB, the increased offset of the attenuation is caused by the constant uniform water layer. Noticeable is the fact that the positions of the minima and maxima have moved. The resulting attenuation caused by the obstacle is minimised for radome thickness λ∕4 and suboptimal for radome thickness λ∕2. The positions of optimal to suboptimal thickness have moved by about λ∕4. By optimising the radome thickness for the largest possible water layer, the performance can be increased by almost 3 dB for one-way and 6 dB for return. Regarding the transferability of the results for the 1 mm water layer optimisation to different water layer thicknesses. The local minimum of the attenuation at radome thicknesses of about λ∕4 remains, if the water layer thicknesses are at least as thick as stated in Table 1. Hence, for the given 24 GHz optimisation example, the same results can be obtained for thicker water layers (dW>1 mm), however, since multi-path propagation and interference have higher impacts for dW<1 mm, the position of the minimum wanders towards a optimal radome thickness of about λ∕2 if the conditions of Table 1 are not met.
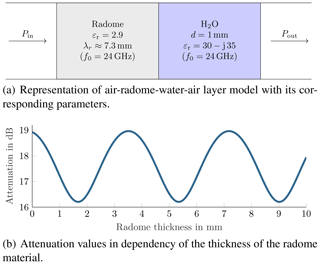
Figure 10Simulation setup for radome with constant water layer contemplation with the associated attenuation graph.
Summarizing the result of the given example. The traditional way of optimising the radome allows to increase the dynamic range by about 1.2 dB, but only without a cover layer. The presented optimisation which considers also performance degrading sediment layers, allows to increase the system dynamic range by almost 3 dB with presence of a worst-case cover layer, but loses 1.2 dB without cover layer. However, this effect is even useful for the overall system design. The realistic air-radome-water-air example would have a total maximum attenuation of 19 dB if optimised with the traditional approach. The radome optimisation including the cover layer decreases the maximum attenuation to almost 16 dB. Bringing that increase of the performance in context to the two-way attenuation of the overall system, then the dynamic range is increased by about 6 dB. An increase of 6 dB allows the radar system to detect an object that is a quarter the size (virtual size represented by the RCS), as compared with the traditional radome optimisation.
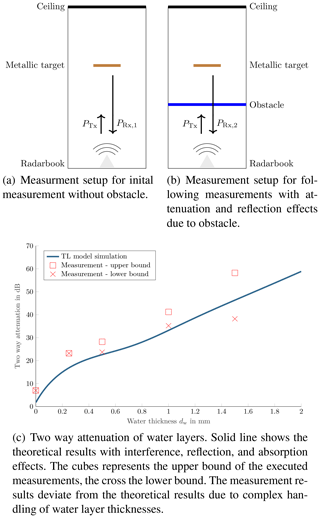
To obtain relative results, the experimental setups of the Fig. 11a and b have been employed. Here, the radar system is positioned on the ground, looking upwards. As reference object a metallic target, such as a corner reflector is utilised. The corner reflector is positioned on a stand at a predefined distance. The first measurement is carried out and the echoed power of the corner reflector is evaluated. The following measurements include an obstacle, the alteration in the reflected power can then be attributed accordingly to the obstacle. For the correct assignment of the reflected power to the metallic target, it is essential to minimise the effects of standing waves between transceiver, obstacle, and ceiling. Hence, the modulation parameters of the radar system have been optimised and an application specific post-processing has been applied. Figure 11c shows the measured two-way attenuation of water for different water layer thicknesses. Several measurements have been carried out, the result area is plotted with its maximum and minimum values. The cubes represent the upper bound of the executed measurements, the crosses the lower bound. The solid blue line shows the aforementioned theoretical results including interference, reflection, and absorption effects. The measured results and the theoretical results deviate due to the complex handling and modelling of water layers, especially the thickness. Since the employed radar hardware has a spatially extended patch antenna with several channels, the uniform water layer must be equally distributed over the whole area. The deviation originates from the surface tension of water, manufacturing accuracies, and the overall sum of smaller effects. The discrepancy at zero water layer thickness results from the experimental setup for introducing the water layer within the reactive near-field. However, the results are reproducible in terms of measurement and computational accuracy.
This paper was focused on the signal degradation of radar-based safety-critical sensors due to sediments and external influences. New applications may expose sensor systems to such climatic and environmental phenomena. To assure operationality, these signal affecting effects have to be taken into consideration. The proposed TL-based model helps to evaluate worst-case scenarios. Measurement and simulation results show that the model is applicable and performant. The underlying material data helps remarkably for the evaluation of relevant covering layers. The practical example demonstrates that the proposed optimisation by employing the TL-model allows to increase the sensor performance by up to 6 dB under worst-case conditions.
The underlying research data can be requested from the authors.
US and MGE conceived the presented concept. ED, MM, and MG Ehrnsperger implemented the model and performed the computations. US, MM, and MGE verified the analytical methods. MM and MGE carried out the experiments. MGE wrote the manuscript in consultation with US and TFE. TFE supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Kleinheubacher Berichte 2018”. It is a result of the Kleinheubacher Tagung 2018, Miltenberg, Germany, 24–26 September 2018.
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
This paper was edited by Romanus Dyczij-Edlinger and reviewed by three anonymous referees.
Ansari, A. J. and Evans, B. G. : Microwave Propagation in Sand and Dust Storms, in: IEEE Proceedings F Communications, Radar and Signal Processing, 129, 315–322, 1982. a
Arage, A., Steffens, W. M., Kuehnle, G., and Jakoby, R.: Effects of Water and Ice Layer on Automotive Radar, Robert Bosch GmbH, 2006. a
Ari, S., Ebbe, N., and Martti, T.: Mixing Formulae and Experimental Results for the Dielectric Constant of Snow, J. Glaciol., 31, 163–170, 1985. a, b
Chen, H.-Y. and Ku, C.-C.: Calculation of Wave Attenuation in Sand and Dust Storms by the FDTD and Turning Bands Methods at 10–100 GH, IEEE T. Antenn. Propag., 60, 2951–2960, 2012. a
Hallikainen, M.: Microwave Dielectric Properties of Materials, in Encyclopedia of Remote Sensing, Encyclopedia of Earth Sciences Series, New York, NY, Springer New York, 364–374, 2014. a
Jun, L., Shaojie, Z., Lingmei, J., Linna, C., and Fengmin, W.: The Influence of Organic Matter on Soil Dielectric Constant at Microwave Frequencies (0.5–40 GHz), IEEE T. Geosci. Remote, 13–16, 2013. a, b
Liebe, H. J., Hufford, G. A., and Manabe, T.: A Model for the Complex Permittivity of Water at Frequencies below 1 TH, Int. J. Infrared Milli., 12, 659–675, 1991. a
Martti, T. H., Fawwaz, T. U., and Mohamed, A.: ielectric Properties of Snow in the 3 to 37 GHz, IEEE T. Antenn. Propag., 34, 1329–1340, 1986. a, b, c
Matzler, C.: Microwave (1–100 GHz) Dielectric Model of Leave, IEEE T. Geosci. Remote, 32, 947–949, 1994. a, b, c
Matzler, C., Aebischer, H., and Schanda, E.: Microwave Dielectric Properties of Surface Snow, IEEE J. Oceanic Eng., 9, 366–371, 1984. a
Mironov, V. L., Dobson, M. C., Kaupp, V. H., Komarov, S. A., and Kleshchenko, V. N.: Generalized Refractive Mixing Dielectric Model for Moist Soils, IEEE T. Geosci. Remote, 42, 773–785, 2004. a
Myron, C. D., Fawwaz,T. U., Martti, T. H., and Mohamed, A. E.-L.: Microwave Dielectric Behaviour of Wet Soil – Part II, Dielectric mixing model, IEEE T. Geosci. Remote, 23, 35–46, 1985. a, b
Pfeiffer, F.: Analyse und Optimierung von Radomen für automobile Radarsensoren, Doctoral Thesis, Technical University of Munich, Munich, 53 pp., 2010. a
Quan, C., Jiangyuan, Z., and Ping, Z.: The Simplified Model of Soil Dielectric Constant and Soil Moisture at the Main Frequency Points of Microwave Band, IEEE T. Geosci. Remote, 2712–2715, 2013. a
Schelkunoff, S. A.: Electromagnetic Waves, Toronto, New York, London, D. Van Nostrand Company, Inc., 26 pp., 1951 a
Schmugge, T., Wang, J., and Williams, D.: Dielectric Constants of Soils at Microwave Frequencies – II, NASA Technical Paper, 1238, 1–38, 1978. a
Shuji, F., Takeshi, M., Shigenori, M., and Shinji, M.: The Measurement on the Dielectric Properties of Ice at HF, VHF and Microwave Frequencies, IEEE T. Geosci. Remote, 3, 1258–1260, 1993. a
Shuji, F., Takeshi, M., and Shinji, M.: Dielectric Properties of Ice Containing Ionic Impurities at Microwave Frequencies, IEEE T. Geosci. Remote, 101, 6219–6222, 1997. a
Tiuri, M., Sihvola, A., Nyfors, E., and Hallikaiken, M.: The Complex Dielectric Constant of Snow at Microwave Frequencies, IEEE J. Oceanic Eng., 9, 377–382, 1984. a
Vladimir, V. T.: Model of Complex Dielectric Constant of Wet and Frozen Soil in the 1–40 GHz Frequency Range, IEEE T. Geosci. Remote, 3, 1576–1578, 1994. a
Wolfgang, P. and Speckmann, H.: Radarsensoren: neue Technologien zur präisen Bestandsführung; T. 1, Grundlagen und Messung der Bodenfeuchte, Landbauforsch. Volk., 54, 73–86, 2004. a